粒子群PSO优化算法学习笔记（附讲解如何使用python语言sko.PSO工具包）

算法描述

粒子群算法思想来源于实际生活中鸟捕食的过程。假设在一个n维的空间中，有一群鸟（m只）在捕食，食物位于n维空间的某个点上，对于第i只鸟某一时刻来说，有两个向量描述，一个是鸟的位置向量，第二个是鸟的速度。假设鸟能够判断一个位置的好坏，所谓“好坏”，就是离食物更近了还是更远了。鸟在捕食的过程中会根据自己的经验以及鸟群中的其他鸟的位置决定自己的速度，根据当前的位置和速度，可以得到下一刻的位置，这样每只鸟通过向自己和鸟群学习不断的更新自己的速度位置，最终找到食物，或者离食物足够近的点。更新速度和位置的表达式如下。

其效果图见下面：

sko.PSO 工具包讲解

python语言
首先要下载这个工具包。
这个anaconda下载大家都会
参数详解
如代码：
pso = PSO(func=demo_func, dim=3, pop=40, max_iter=150, lb=[0, -1, 0.5], ub=[1, 1, 1], w=0.8, c1=0.5, c2=0.5)

参数	说明
func	类型function， 所要求得优化函数
dim	类型int，维数，即函数的参数数
pop	类型int,种群的大小，也就是粒子的数量。我们使用“pop”来与GA保持一致。默认40
max_iter	类型int,iter迭代的最大值 默认150
lb	类型列表,下限。每个参数的下限
ub	类型列表,上限。每个参数的上限
W	对应公式里的惯性权重，默认0.8
C1	学习因子1，默认0.5
C2	学习因子2，默认0.5

属性	说明
pbest_x	array_like, shape is (pop,dim)历史上每个粒子的最佳位置
pbest_y	array_like, shape is (pop,1)历史上最好的粒子图像
gbest_x	array_like, shape is (1,dim)general best location for all particles in history
gbest_y	float历史上所有粒子的最佳图像
gbest_y_hist	list每个迭代的gbest_y

算例：有限制的粒子群

来源于官方文档例子

第一步，定义问题

def demo_func(x):
    x1, x2, x3 = x
    return x1 ** 2 + (x2 - 0.05) ** 2 + x3 ** 2

第二步，做粒子群算法

from sko.PSO import PSO

pso = PSO(func=demo_func, dim=3, pop=40, max_iter=150, lb=[0, -1, 0.5], ub=[1, 1, 1], w=0.8, c1=0.5, c2=0.5)
pso.run()
print('best_x is ', pso.gbest_x, 'best_y is', pso.gbest_y)

结果：

可以发现x的值落在啦限制区间内。
第三步，画出结果

import matplotlib.pyplot as plt

plt.plot(pso.gbest_y_hist)
plt.show()

算例：无限制的粒子群

def demo_func(x):
    x1, x2, x3 = x
    return x1 ** 2 + (x2 - 0.05) ** 2 + x3 ** 2


# %% Do PSO
from sko.PSO import PSO

pso = PSO(func=demo_func, dim=3)
pso.run()
print('best_x is ', pso.gbest_x, 'best_y is', pso.gbest_y)

# %% Plot the result
import matplotlib.pyplot as plt

plt.plot(pso.gbest_y_hist)
plt.show()

结果：


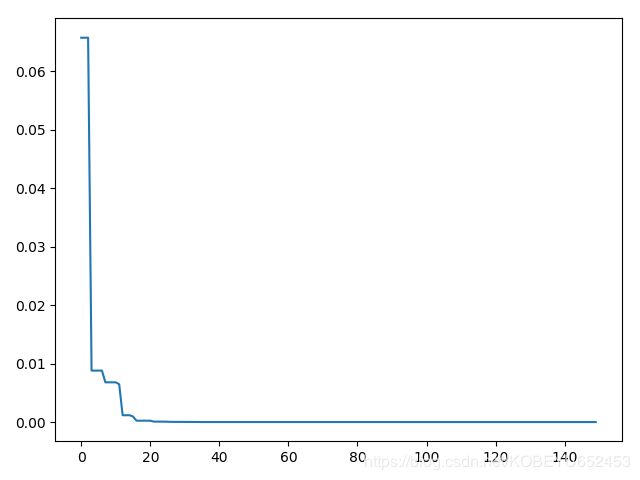
可以发现x1的值无限接近0，x2无限接近0.05,x3的值无限接近0.

所谓优化，我的理解是对一个问题求出它足够好的解，即使这个解不是最优解。如题中解接近0而不是0。在现实生活中，这个解满足要求。

其他专业的计算机小白，写博文不容易。如果你觉得本文对你有用，请点个赞支持下。谢谢