1、用带权的邻接矩阵c来表示带权有向图, c[i][j]表示弧上的权值。设S为已知最短路径的终点的集合,它的初始状态为空集。从源点v经过S到图上其余各点vi的当前最短路径长度的初值为:dist[i]=c[v][i], vi属于V;
2、选择vu, 使得dist[u]=Min{dist[i] | vi属于V-S},vj就是长度最短的最短路径的终点。令S=S U{U -{u}};
3、修改从v到集合V-S上任一顶点vi的当前最短路径长度:如果 dist[u]+c[u][j]< dist[j] 则修改 dist[j]=dist[u]+c[u][j];
4、重复操作(2),(3)共n-1次。
1.2 算法实现代码
#include "stdafx.h"
#include
#include
#include
#include
#include
using namespace std;
const int N = 100;
const int M = 1000;
ofstreamfout("D:\\cs.txt");
template<class Type>
void Dijkstra(int n,int v,Typedist[],int prev[],Type c[][N+1]);
void Traceback(int v,int i,int prev[]);//输出最短路径 v源点,i终点
int main()
{
LARGE_INTEGER begin,end,frequency;
QueryPerformanceFrequency(&frequency);
int n,v;
intdist[N+1],prev[N+1],c[N+1][N+1];
cout<<"输入点数、出发点:";
cin>>n>>v;
cout<<"有向图权的矩阵为:"<
for(int i=1; i<=n; i++)
{
for(int j=1; j<=n; j++)
{
c[i][j]=rand()%100+1;
fout<" ";
cout<" ";
}
cout<
fout<
}
QueryPerformanceCounter(&begin);
Dijkstra(n,v,dist,prev,c);
QueryPerformanceCounter(&end);
for(int i=1; i<=n; i++)
{
if(i!=v)
{
cout<<"源点"<"到点"<"的最短路径长度为:"<",其路径为";
Traceback(v,i,prev);
cout<
}
}
cout<<"时间:"
<<((double)(end.QuadPart- begin.QuadPart) / frequency.QuadPart)*1000
<<"ms"<
return0;
}
template<class Type>
void Dijkstra(int n,int v,Typedist[],int prev[],Type c[][N+1])
{
bools[N+1];
for(int i=1; i<=n; i++)
{
dist[i] = c[v][i];//dist[i]表示当前从源到顶点i的最短特殊路径长度
s[i] = false;
if(dist[i]== M)
{
prev[i] = 0;//记录从源到顶点i的最短路径i的前一个顶点
}
else
{
prev[i] = v;
}
}
dist[v] = 0;
s[v] = true;
for(int i=1; i
{
inttemp = M;
int u =v;//上一顶点
//取出V-S中具有最短特殊路径长度的顶点u
for(int j=1; j<=n; j++)
{
if((!s[j])&& (dist[j]
{
u = j ;
temp = dist[j];
}
}
s[u] = true;
//根据作出的贪心选择更新Dist值
for(int j=1; j<=n; j++)
{
if((!s[j])&& (c[u][j]
{
Type newdist = dist[u] +c[u][j];
if(newdist< dist[j])
{
dist[j] = newdist;
prev[j] = u;
}
}
}
}
}
//输出最短路径 v源点,i终点
void Traceback(int v,int i,int prev[])
{
if(v == i)
{
cout<
return;
}
Traceback(v,prev[i],prev);
cout<<"->"<
}
1.3 计算复杂性
对于一个具有n个顶点和e条边的带权有向图,如果用带权邻接矩阵表示这个图,那么Dijkstra算法的主循环体需要O(n)时间。这个循环需要执行n-1次,所以完成循环需要O(n^2)时间。算法的其余部分所需要的时间不超过O(n^2)。
1.4 运行结果
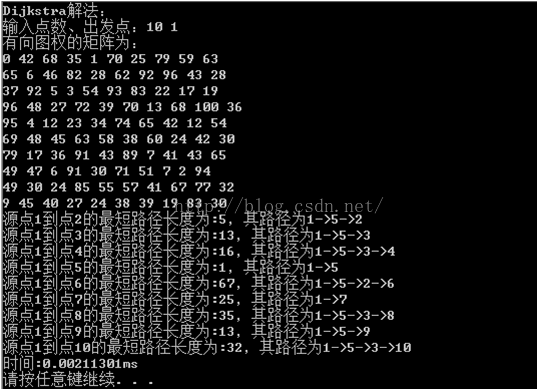
2 分支限界法
2.1 分支限界法解决单源最短路径问题描述
采用广度优先产生状态空间树的结点,并使用剪枝函数的方法称为分枝限界法。所谓“分支”是采用广度优先的策略,依次生成扩展结点的所有分支(即:儿子结点)。所谓“限界”是在结点扩展过程中,计算结点的上界(或下界),边搜索边减掉搜索树的某些分支,从而提高搜索效率
按照广度优先的原则,一个活结点一旦成为扩展结点(E-结点)R后,算法将依次生成它的全部孩子结点,将那些导致不可行解或导致非最优解的儿子舍弃,其余儿子加入活结点表中。然后,从活结点表中取出一个结点作为当前扩展结点。重复上述结点扩展过程,直至找到问题的解或判定无解为止。
2.2 分支限界法算法思想描述
算法从图G的源顶点s和空优先队列开始。结点s被扩展后,它的儿子结点被依次插入堆中。此后,算法从堆中取出具有最小当前路长的结点作为当前扩展结点,并依次检查与当前扩展结点相邻的所有顶点。如果从当前扩展结点i到顶点j有边可达,且从源出发,途经顶点i再到顶点j的所相应的路径的长度小于当前最优路径长度,则将该顶点作为活结点插入到活结点优先队列中。这个结点的扩展过程一直继续到活结点优先队列为空时为止。
在算法扩展结点的过程中,一旦发现一个结点的下界不小于当前找到的最短路长,则算法剪去以该结点为根的子树。
在算法中,利用结点间的控制关系进行剪枝。从源顶点s出发,2条不同路径到达图G的同一顶点。由于两条路径的路长不同,因此可以将路长长的路径所对应的树中的结点为根的子树剪去。
2.3 算法实现代码
#include "stdafx.h"
#include "MinHeap.h"
#include
#include
#include
#include
using namespace std;
ifstreamfin("D:\\cs.txt");
template<class Type>
class Graph
{
friend int main();
public:
voidShortesPaths(int);
private:
int n, //图G的顶点数
*prev; //前驱顶点数组
Type **c, //图G的领接矩阵
*dist; //最短距离数组
};
template<class Type>
class MinHeapNode
{
friendGraph;
public:
operatorint ()const{return length;}
private:
int i; //顶点编号
Type length; //当前路长
};
template<class Type>
voidGraph::ShortesPaths(int v)//单源最短路径问题的优先队列式分支限界法
{
MinHeap>H(1000);
MinHeapNode E;
//定义源为初始扩展节点
E.i=v;
E.length=0;
dist[v]=0;
while (true)//搜索问题的解空间
{
for (int j = 1; j <= n; j++)
if((c[E.i][j]!=0)&&(E.length+c[E.i][j]
// 顶点i到顶点j可达,且满足控制约束
dist[j]=E.length+c[E.i][j];
prev[j]=E.i;
// 加入活结点优先队列
MinHeapNodeN;
N.i=j;
N.length=dist[j];
H.Insert(N);
}
try
{
H.DeleteMin(E); // 取下一扩展结点
}
catch (int)
{
break;
}
if(H.currentsize==0)// 优先队列空
{
break;
}
}
}
void Traceback(int v,int i,int prev[])
{
if(v == i)
{
cout<
return;
}
Traceback(v,prev[i],prev);
cout<<"->"<
}
int main()
{
LARGE_INTEGER begin,end,frequency;
QueryPerformanceFrequency(&frequency);
intprev[102] ;
intdist[102];
intn,original;
cout<<"输入点数、出发点:";
cin>>n>>original;
cout<<"单源图的邻接矩阵如下:"<
int **c = new int*[n+1];
for(int i=0;i
{
prev[i]=0;
dist[i]=1000;
}
for(int i=1;i<=n;i++)
{
c[i]=newint[n+1];
for(int j=1; j<=n; j++)
{
fin>>c[i][j];
cout<" ";
}
cout<
}
intv=original;
Graph<int>G;
G.n=n;
G.c=c;
G.dist=dist;
G.prev=prev;
QueryPerformanceCounter(&begin);
G.ShortesPaths(v);
QueryPerformanceCounter(&end);
for (int i = 1; i <= n; i++)
{
if(i!=original)
{
cout<<"源点"<"到点"<"的最短路径长度为:"<",其路径为";
Traceback(original,i,prev);
cout<
}
}
for(int i=1;i<=n;i++)
{
delete[]c[i];
}
delete[]c;
c=0;
cout<<"时间:"
<<((double)(end.QuadPart- begin.QuadPart) / frequency.QuadPart )*1000
<<"ms"<
return0;
}
2.4 算法复杂度
经过分析可知算法的时间复杂度:O(n!),空间复杂度:O(n*n)。
2.5 运行结果
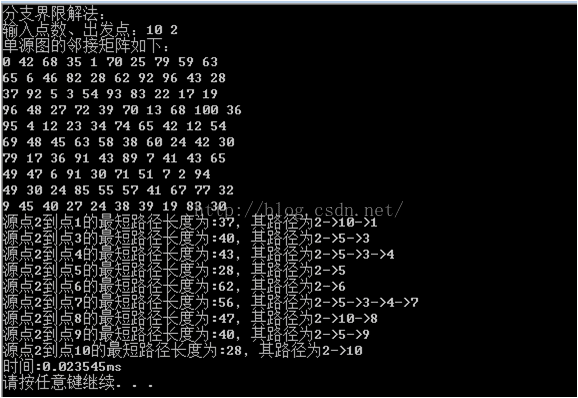
3 Bellman-Ford算法
3.1 算法思想
Bellman-Ford算法能在更普遍的情况下(存在负权边)解决单源点最短路径问题。对于给定的带权(有向或无向)图 G=(V,E),其源点为s,加权函数 w是 边集 E 的映射。对图G运行Bellman-Ford算法的结果是一个布尔值,表明图中是否存在着一个从源点s可达的负权回路。若不存在这样的回路,算法将给出从源点s到 图G的任意顶点v的最短路径d[v]。
3.2 算法实现步骤
Bellman-Ford算法流程分为三个阶段:
(1)初始化:将除源点外的所有顶点的最短距离估计值 d[v]←+∞, d[s] ←0;
(2)迭代求解:反复对边集E中的每条边进行松弛操作,使得顶点集V中的每个顶点v的最短距离估计值逐步逼近其最短距离;(运行|v|-1次)
(3)检验负权回路:判断边集E中的每一条边的两个端点是否收敛。如果存在未收敛的顶点,则算法返回false,表明问题无解;否则算法返回true,并且从源点可达的顶点v的最短距离保存在 d[v]中。
3.3 算法实现代码
#include "stdafx.h"
#include
#include
#include
#include
#include
using namespace std;
#define MAX0x3f3f3f3f
#define N100000
int nodenum, edgenum=0,original; //点,边,起点
typedef struct Edge //边
{
int u,v;
intcost;
}Edge;
Edgeedge[N];
int dis[N],pre[N];
bool Bellman_Ford()
{
for(int i = 1; i <= nodenum; ++i) //初始化
dis[i] = (i == original ? 0 :MAX);
for(int i = 1; i <= nodenum - 1; ++i)
for(int j = 1; j <= edgenum; ++j)
if(dis[edge[j].v]> dis[edge[j].u] + edge[j].cost) //松弛
{
dis[edge[j].v] = dis[edge[j].u]+ edge[j].cost;
pre[edge[j].v] =edge[j].u;
}
boolflag = 1; //判断是否含有负权回路
for(int i = 1; i <= edgenum; ++i)
if(dis[edge[i].v]> dis[edge[i].u] + edge[i].cost)
{
flag = 0;
break;
}
returnflag;
}
void print_path(int root) //打印最短路的路径(反向)
{
while(root!= pre[root]) //前驱
{
printf("%d<-",root);
root = pre[root];
}
if(root ==pre[root])
printf("%d\n",root);
}
ifstreamfin("D:\\cs.txt");
int main()
{
LARGE_INTEGERbegin,end,frequency;
QueryPerformanceFrequency(&frequency);
int k,sign;
cout<<"输入点数、出发点:";
cin>>nodenum>>original;
pre[original] = original;
for(int i=1; i<=nodenum; i++)
{
for(int j=1; j<=nodenum; j++)
{
fin>>k;
if(k)
{
edgenum++;
edge[edgenum].u=i;
edge[edgenum].v=j;
edge[edgenum].cost=k;
}
elsecontinue;
cout<"";
}
cout<
}
QueryPerformanceCounter(&begin);
sign= Bellman_Ford();
QueryPerformanceCounter(&end);
if(sign)
for(int i = 1; i <= nodenum; ++i) //每个点最短路
{
if(i!=original)
{
printf("节点%3d到节点%3d最短路长度为:",original,i);
printf("%d\t",dis[i]);
printf("最短路径为:");
print_path(i);
}
}
else
printf("图中存在负权回路\n");
cout<<"时间:"
<<(double)(end.QuadPart- begin.QuadPart) / frequency.QuadPart
<<"s"<
return0;
}
3.4 算法复杂度分析
求单源最短路,可以判断有无负权回路(若有,则不存在最短路),时效性较好,时间复杂度O(VE)。
3.5 运行结果:

4 SPFA算法
4. 1 算法介绍
SPFA(Shortest Path FasterAlgorithm)(队列优化)算法是求单源最短路径的一种算法,它还有一个重要的功能是判负环(在差分约束系统中会得以体现),在Bellman-ford算法的基础上加上一个队列优化,减少了冗余的松弛操作,是一种高效的最短路算法。
4.2 算法实现步骤
我们用数组d记录每个结点的最短路径估计值,而且用邻接表来存储图G。我们采取的方法是动态逼近法:设立一个先进先出的队列用来保存待优化的结点,优化时每次取出队首结点u,并且用u点当前的最短路径估计值对离开u点所指向的结点v进行松弛操作,如果v点的最短路径估计值有所调整,且v点不在当前的队列中,就将v点放入队尾。这样不断从队列中取出结点来进行松弛操作,直至队列空为止。
4.3 算法实现代码
#include"stdafx.h"
#include
#include
#include
#include
#include
#include
using namespace std;
struct Edge
{
intto,length;
};
bool spfa(const int &beg,const vector >&adjlist,vector<int>&dist,vector<int> &path)
{
const int &INF=0x7FFFFFFF,&NODE=adjlist.size();//用邻接表的大小传递顶点个数,减少参数传递
dist.assign(NODE,INF);//初始化距离为无穷大
path.assign(NODE,-1);//初始化路径为未知
deque<int>que(1,beg);//处理队列
vector<bool>flag(NODE,0);//标志数组,判断是否在队列中
vector<int>cnt(NODE,0);//记录各点入队次数,用于判断负权回路
dist[beg]=0;//出发点到自身路径长度为0
++cnt[beg];//开始计数
flag[beg]=1;//入队
while(!que.empty())
{
const int now=que.front();//当前处理的点,由于后面被删除,不可定义成常量引用
que.pop_front();
flag[now]=0;//将该点拿出队列
for(int i=0; i!=adjlist[now].size(); ++i)//遍历所有与当前点有路径的点
{
constint &next=adjlist[now][i].to;//目标点,不妨定义成常量引用,稍稍快些
if(dist[now]
dist[next]>dist[now]+adjlist[now][i].length)//优于当前值
{
dist[next]=dist[now]+adjlist[now][i].length;//更新
path[next]=now;//记录路径
if(!flag[next])//若未在处理队列中
{
if(++cnt[next]==NODE)return 1;//计数后出现负权回路
if(que.empty()||//空队列
dist[next]
que.push_front(next);//放在队首
elseque.push_back(next);//否则放在队尾
flag[next]=1;//入队
}
}
}
}
return0;
}
ifstreamfin("D:\\cs.txt");
int main()
{
LARGE_INTEGER begin,end,frequency;
QueryPerformanceFrequency(&frequency);
intn_num,e_num,beg,k,sign;
cout<<"输入点数、出发点:";
cin>>n_num>>beg;
beg--;
vector >adjlist(n_num,vector());//默认初始化邻接表
cout<<"有向图权的矩阵为:"<
Edge tmp;intp,m;
for(int i=0; i
{
for(int j=0; j
{
p=i;
fin>>k;
cout<"";
if(k){
tmp.length=k;
tmp.to=j;
adjlist[p].push_back(tmp);
}
}
cout<
}
vector<int>dist,path;//用于接收最短路径长度及路径各点
QueryPerformanceCounter(&begin);
sign =spfa(beg,adjlist,dist,path);
QueryPerformanceCounter(&end);
cout<<"时间:"
<<(double)(end.QuadPart- begin.QuadPart) / frequency.QuadPart
<<"s"<
if(sign){cout<<"图中存在负权回路\n";
}
else for(int i=0;i!=n_num; ++i)
{
if(i!=beg)
{cout<"到"<"的最短距离为"<",反向打印路径:";
for(int w=i; path[w]>=0; w=path[w])
cout<"<-";
cout<'\n';
}
}
return 0;
}
4.4 算法复杂度分析
期望时间复杂度:O(me),其中m为所有顶点进队的平均次数,可以证m一般小于等于2。算法编程后实际运算情况表明m一般没有超过2n。事实上顶点入队次数m是一个不容易事先分析出来的数,但它确是一个随图的不同而略有不同的常数。所谓常数,就是与e无关,与n也无关,仅与边的权值分布有关.一旦图确定,权值确定,原点确定。
4.5 运行结果
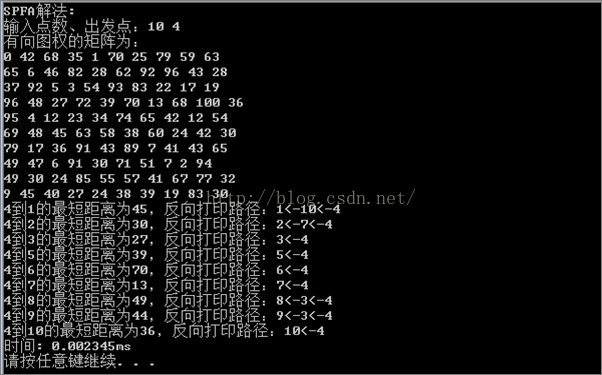
三、 四种算法性能比较
1 时间复杂度总结
| 算法 |
Dijkstra |
分支界限 |
Bellman-Ford |
SPFA |
| 时间复杂度 |
O(V*V+E) |
O(V!) |
O(V*E) |
O(V*E) |
2 分析
(1) 求单源、无负权的最短路。时效性较好,时间复杂度为O(V*V+E)。源点可达的话,O(V*lgV+E*lgV)=>O(E*lgV)。当是稀疏图的情况时,此时E=V*V/lgV,所以算法的时间复杂度可为O(V^2) 。
(2)与Dijkstra算法不同的是,在Bellman-Ford算法中,边的权值可以为负数。设想从我们可以从图中找到一个环路(即从v出发,经过若干个点之后又回到v)且这个环路中所有边的权值之和为负。那么通过这个环路,环路中任意两点的最短路径就可以无穷小下去。如果不处理这个负环路,程序就会永远运行下去。而Bellman-Ford算法具有分辨这种负环路的能力。
(3)SPFA算法是Bellman-Ford的队列优化,时效性相对好,时间复杂度O(kE)。(k<)。
与Bellman-ford算法类似,SPFA算法采用一系列的松弛操作以得到从某一个节点出发到达图中其它所有节点的最短路径。所不同的是,SPFA算法通过维护一个队列,使得一个节点的当前最短路径被更新之后没有必要立刻去更新其他的节点,从而大大减少了重复的操作次数。SPFA算法可以用于存在负数边权的图,这与Dijkstra算法是不同的。与Dijkstra算法与Bellman-ford算法都不同,SPFA的算法时间效率是不稳定的,即它对于不同的图所需要的时间有很大的差别。在最好情形下,每一个节点都只入队一次,则算法实际上变为广度优先遍历,其时间复杂度仅为O(E)。另一方面,存在这样的例子,使得每一个节点都被入队(V-1)次,此时算法退化为Bellman-ford算法,其时间复杂度为O(VE)。
3 效率的验证
(1)为了能够说明问题,本实验中在对四种算法进行比较的时候,运用共同的测试数据,于是我采取的方法是先在一种算法中随机产生有向图的矩阵信息,保存在一个文本文件中,其他算法进行测试的时候,用同样的数据进行测试。
(2)如下图所示产生了一组测试数据,这组数据是一个10行10列的矩阵,代表着有10个节点的图的矩阵,同时对于同样的数据四种算法的运行结果分别如下图所示:

Dijkstra算法运行结果

分支界限算法运行结果
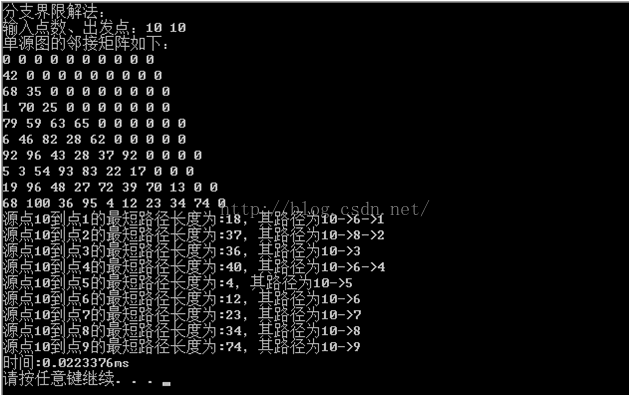
Bellman-Ford算法运行结果

SPFA算法运行结果
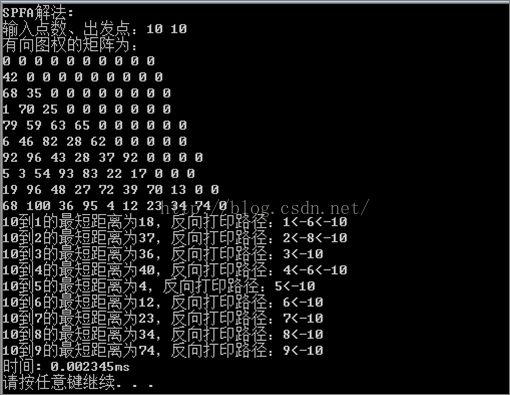
(3)从以上实验结果可以看出,对于同一组测试数据,运用不同的算法,所得的结果是一样的,只是运行时间有所区别,可见,所设计的算法是正确,有效的。
(4)为了方便直观的比较不同算法所用的时间效率,在此,产生了100行100列的图的矩阵,作为测试数据。如下TXT文件所示,
同时选取了不同规模的数据作为测试数据,测试不同算法所运行的时间,时间的单位是MS,制作表格如下,
Dijkstra算法运行时间统计
|
|
100 |
80 |
60 |
50 |
30 |
10 |
| Dijkstra |
0.133 |
0.070 |
0.046 |
0.034 |
0.020 |
0.002 |
分支界限算法算法运行时间统计
|
|
100 |
80 |
60 |
50 |
30 |
10 |
| 分支界限 |
3.143 |
1.599 |
0.727 |
0.685 |
0.457 |
0.015 |
Bellman-Ford算法运行时间统计
|
|
100 |
80 |
60 |
50 |
30 |
10 |
| Bellman-Ford |
0.540 |
0.413 |
0.378 |
0.203 |
0.130 |
0.040 |
SPFA算法运行时间统计
|
|
100 |
80 |
60 |
50 |
30 |
10 |
| SPFA |
0.133 |
0.070 |
0.046 |
0.034 |
0.020 |
0.002 |
(5) 由以上程序运行结果可以看出,随着问题规模也就是图中节点数目的增加,运用四种算法求解所需要的时间都增加了。这正好验证了我们所分析的四种算法理论的时间复杂度都和节点数目V有关。
(6) 同时可以看见分支界限算法所需时间明显比Dijkstra算法算法要多,这从他们的时间复杂度表达式可以看出,同时由于SPFA算法是用队列对Bellman-Ford算法进行的优化,所以时间复杂度也要小些,也验证了我们理论分析的时间复杂度的正确性。
(7) 同时通过实验也发现,图的稀疏程度对四种算法的求解影响也不相同,为此,特产生了一个比较稀疏的图的矩阵。如下图所示,其中0代表两个节点之间不直接想通,这样就减少了很多的边数,变成了一个比较稀疏的图。节点的数目仍然是50。
50个节点的密集图
| 算法 |
Dijkstra |
分支界限 |
Bellman-Ford |
SPFA |
| 时间 |
0.034 |
0.203 |
0.685 |
0.034 |
50个节点的稀疏图
| 算法 |
Dijkstra |
分支界限 |
Bellman-Ford |
SPFA |
| 时间 |
0.014 |
0.198 |
0.015 |
0.002 |
(8)对比以上两个表可知,随着边数的急剧减少,Dijkstra算法,Bellman-Ford算法,SPFA算法三种算法的时间都显著减少了,只而分支界限算法的时间基本没变多少。由于分支界限算法的时间复杂度表达式中没有涉及到边E,其他三种算法都和边E有关,所以试验结果也很好的说明了这个问题。
(9) Dijkstra算法的适用范围是图的权值为非负值,其他三种算法可以针对负数的权值,同时Bellman-Ford算法和SPFA算法还可以检查图中是否存在负权回路,如图所示:

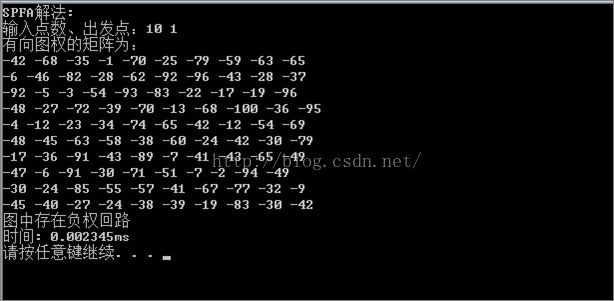
4 说明
(1)Dijkstra:适用于权值为非负的图的单源最短路径。
(2)Bellman-Ford:适用于权值有负值的图的单源最短路径,并且能够检测负圈。
(3)SPFA:适用于权值有负值,且没有负圈的图的单源最短路径。












