PCL—基于凹凸性的点云分割算法详解

参考：https://www.cnblogs.com/ironstark/p/5027269.html

1. 图像分割的两条思路

• 场景分割是机器视觉中的重要任务，尤其对家庭机器人而言，优秀的场景分割算法是实现复杂功能的基础。图像分割的做法大概有两种：剑宗——自底向上：先将图像聚类成小的像素团再慢慢合并；气宗——自顶向下：用多尺度模板分割图像，再进一步将图像优化分割成不同物体。当然，还有将二者合而为一的方法：training with data set，这第三种方法也不好，太依赖于已知的物体而失去了灵活性。家庭机器人面对家里越来越多的东西需要一种非训练且效果很好的分割法。《Object Partitioning using Local Convexity 》一文的作者从古籍中（也不老，1960s左右吧），找到了一种基于凹凸性的分割方法。实际上基于凹凸的图像理解在之前是被研究过的，但是随着神经网络的出现，渐渐这种从明确物理意义入手的图像"理解"方法就被淹没了。对于二维图像而言，其凹凸性较难描述，但对于三维图像而言，凹凸几乎是与生俱来的性质。

2. LCCP方法

• LCCP是 Locally Convex Connected Patches 的缩写，翻译成中文叫做 ”局部凸连接打包一波带走“… …算法大致可以分成两个部分：1.基于超体聚类的过分割；2.在超体聚类的基础上再聚类。超体聚类作为一种过分割方法，在理想情况下是不会引入错误信息的，也就是说适合在此基础上再进行处理。关于超体聚类的相关内容参见上一篇博客：PCL—超体聚类点云分割算法详解。
• LCCP方法并不依赖于点云颜色，所以只使用空间信息和法线信息，wc=0，ws=1，wn=4。

2.1 算法理论

• 点云完成超体聚类之后，对于过分割的点云需要计算不同的块之间凹凸关系。凹凸关系通过 CC（Extended Convexity Criterion） 和 SC （Sanity criterion） 判据来进行判断。其中 CC 利用相邻两片中心连线向量与法向量夹角来判断两片是凹是凸。显然，如果图中a1>a2则为凹，反之则为凸。
  
• 考虑到测量噪声等因素，需要在实际使用过程中引入门限值（a1需要比a2大出一定量）来滤除较小的凹凸误判。此外，为去除一些小噪声引起的误判，还需要引入“第三方验证”：如果某块和相邻两块都相交，则其凹凸关系必相同。CC 判据最终如 CCe：
  
  
• 如果相邻两面中，有一个面是单独的，CC 判据是无法将其分开的。举个简单的例子，两本厚度不同的书并排放置，视觉算法应该将两本书分割开。如果是台阶，则视觉算法应该将台阶作为一个整体。本质上就是因为厚度不同的书存在 surface-singularities。为此需要引入 SC 判据，来对此进行区分。
  
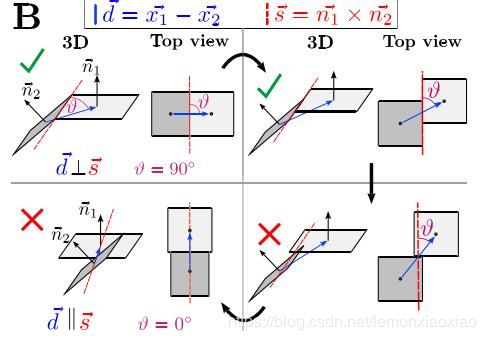
• 如图所示，相邻两面是否真正联通，是否存在单独面，与θ角有关，θ角越大，则两面真的形成凸关系的可能性就越大。据此，可以设计 SC 判据：
  
  
  
  其中 S(向量)为两平面法向量的叉积。
• 最终，两相邻面之间凸边判据为：
  
• 在标记完各个小区域的凹凸关系后，则采用区域增长算法将小区域聚类成较大的物体。此区域增长算法受到小区域凹凸性限制，即：只允许区域跨越凸边增长。
• 至此，分割完成，在滤除多余噪声后即获得点云分割结果。此外：考虑到RGB-D图像随深度增加而离散，难以确定八叉树尺寸，故在z方向使用对数变换以提高精度。分割结果如图：
  
  
  从图中可知，纠缠在一起，颜色形状相近的物体完全被分割开了，如果是图像分割要达到这个效果，那就… …呵呵呵… …

2.2 PCL对该算法的实现

官网并未给出具体实现并测试，我不对以下代码有效性负责。

1 超体聚类

//设定结晶参数
  float voxel_resolution = 0.008f;
  float seed_resolution = 0.1f;
  float color_importance = 0.2f;
  float spatial_importance = 0.4f;
  float normal_importance = 1.0f;
  
  //生成结晶器
  pcl::SupervoxelClustering<PointT> super(voxel_resolution, seed_resolution);
  //和点云形式有关
  if (disable_transform)
    super.setUseSingleCameraTransform(false);
  //输入点云及结晶参数
  super.setInputCloud(cloud);
  super.setColorImportance(color_importance);
  super.setSpatialImportance(spatial_importance);
  super.setNormalImportance(normal_importance);
  //输出结晶分割结果：结果是一个映射表
  std::map <uint32_t, pcl::Supervoxel<PointT>::Ptr > supervoxel_clusters;
  super.extract(supervoxel_clusters);
  std::multimap<uint32_t, uint32_t> supervoxel_adjacency;
  super.getSupervoxelAdjacency(supervoxel_adjacency);

2 LCCP

//生成LCCP分割器
pcl::LCCPSegmentation<PointT>::LCCPSegmentation LCCPseg;
//输入超体聚类结果
seg.setInputSupervoxels(supervoxel_clusters,supervoxel_adjacency);
//CC效验beta值
seg.setConcavityToleranceThreshold(concavity_tolerance_threshold);
//CC效验的k邻点
seg.setKFactor(k_factor_arg)
//
seg.setSmoothnessCheck(bool_use_smoothness_check_arg,voxel_res_arg,seed_res_arg,smoothness_threshold_arg = 0.1);
//SC效验
seg.setSanityCheck(bool_use_sanity_criterion_arg);
//最小分割尺寸
seg.setMinSegmentSize(min_segment_size_arg)

seg.segment();
seg.relabelCloud(pcl::PointCloud<pcl::PointXYZL> &labeled_cloud_arg);

综上所述，LCCP算法在相似物体场景分割方面有着较好的表现，对于颜色类似但棱角分明的物体可使用该算法（比如X同学仓库里那一堆纸箱）。

3. CPC方法

• CPC 方法的全称为 Constrained Planar Cuts，出自论文《Constrained Planar Cuts - Object Partitioning for Point Clouds 》。和 LCCP 方法不同，此方法的分割对象是 object。此方法能够将物体分成有意义的块：比如人的肢体等。CPC方法可作为 AI 的前处理，作为 Robot Vision 还是显得有些不合适。但此方法不需要额外训练，自底向上的将三维图像分割成有明确意义的部分，是非常admirable的。

3.1 算法理论

• 和其他基于凹凸性的方法相同，本方法也需要先进行超体聚类。在完成超体聚类之后，采用和LCCP 相同的凹凸性判据获得各个块之间的凹凸关系。在获得凹凸性之后，CPC方法所采取的措施是不同的，其操作称为半全局分割 。
• 在分割之前，首先需要生成 EEC(Euclidean edge cloud)， EEC的想法比较神奇，因为凹凸性定义在相邻两个”片“上，换言之，定义在连接相邻两“片”的edge上。将每个edge抽象成一个点云，则得到了附带凹凸信息的点云。如图所示，左图是普通点云，但附带了邻接和凹凸信息。右边是EEC，对凹边赋权值1，其他为0。 此方法称作 weighted RANSAC。
  
  显而易见，某处如果蓝色的点多，那么就越凹，就越应该切开（所谓切开实际上是用平面划分），问题就转化为利用蓝点求平面了。利用点云求一个最可能的平面当然需要请出我们的老朋友 RANSAC。但此处引入一个评价函数，用于评价此次分割的优良程度Sm，其中 Pm 是EEC中的点。
  
• 单纯的 weighted RANSAC 算法并不够，其会导致对某些图形的错误分割，所以作者对此做了第一次“修补"。错误的分割如下图所示：
  
• 此修补方法称作 directional weighted RANSAC。方法的原理很简单，垂直于凹边表面的点具有更高的权重。显然，对于EEC中的凹点，只要取其少量邻点即可估计垂直方向。这种修补后还有一个问题，如果这个分割面过长的情况下，有可能会误伤。如图所示：
  
• 于是有了第二种修补方法，称为：Locally constrained cutting。这种修补方法的原理就更加简单粗暴了，对凹点先进行欧式分割（限制增长上限），之后再在分割所得的子域里进行分割。
• 在修修补补之后，CPC 算法终于可以投入使用了，从测试集的结果来看，效果还是很好的。
  

3.2 PCL对该算法的实现

• 在 PCL 中 CPC 类继承自 LCCP 类，但是这个继承我觉得不好，这两个类之间并不存在抽象与具体的关系，只是存在某些函数相同而已。不如多设一个 凹凸分割类 作为 CPC 类与 LCCP 类的父类，所有的输入接口等都由 凹凸分割类 提供。由 CPC 算法和 LCCP 算法继承凹凸类，作为 凹凸分割 的具体实现。毕竟和 凹凸分割 有关的算法多半是对整体进行分割，和其他点云分割算法区别较大。

//生成CPC分割器
pcl::CPCSegmentation<PointT>::CPCSegmentation seg;
//输入超体聚类结果
seg.setInputSupervoxels(supervoxel_clusters,supervoxel_adjacency);
//设置分割参数
setCutting (max_cuts = 20,
            cutting_min_segments = 0,
            cutting_min_score = 0.16,
            locally_constrained = true,
            directed_cutting = true,
            clean_cutting = false)；
seg.setRANSACIterations(ransac_iterations);
seg.segment();
seg.relabelCloud(pcl::PointCloud<pcl::PointXYZL> &labeled_cloud_arg);