MATLAB最小二乘法拟合曲面
MATLAB最小二乘法拟合高次曲面
- 前言
- 1. **函数文件源码** :
- 2. **解决上述问题**
- 3. **生成源代码**
前言
引用来引用去实在没意思(http://blog.sina.com.cn/s/blog_8702e2b60102x4qg.html),看到的很多最小二乘法拟合曲面方程基本都是基于这样的一个方程,代码也没有什么大的改动。只是应用的时候确实存在很多问题,不太适合实际的问题。
简单分析一下上述参考的源码存在的一些问题。
1. 函数文件源码 :
function [a0, a1, a2, a3, a4, a5] = least_square_surface(x,y,z)
% 初始化矩阵
A = zeros(6,6);
B = zeros(6,1);
% 矩阵赋值(根据最小二乘法对最小二乘矩阵赋值)
for i=1:length(x)
for j = length(y)
A(1,1) = 1+A(1,1);
A(1,2) = x(i,j)+A(1,2);
A(1,3) = y(i,j)+A(1,3);
A(1,4) = x(i,j)^2+A(1,4);
A(1,5) = x(i,j)*y(i,j)+A(1,5);
A(1,6) = y(i,j)^2+A(1,6);
A(2,1) = x(i,j)+A(2,1);
A(2,2) = x(i,j)^2+A(2,2);
A(2,3) = x(i,j)*y(i,j)+A(2,3);
A(2,4) = x(i,j)^3+A(2,4);
A(2,5) = x(i,j)^2*y(i,j)+A(2,5);
A(2,6) = x(i,j)*y(i,j)^2+A(2,6);
A(3,1) = y(i,j)+A(3,1);
A(3,2) = x(i,j)*y(i,j)+A(3,2);
A(3,3) = y(i,j)^2+A(3,3);
A(3,4) = x(i,j)^2+A(3,4);
A(3,5) = x(i,j)*y(i,j)^2+A(3,5);
A(3,6) = y(i,j)^3+A(3,6);
A(4,1) = x(i,j)^2+A(4,1);
A(4,2) = x(i,j)^3+A(4,2);
A(4,3) = x(i,j)^2*y(i,j)+A(4,3);
A(4,4) = x(i,j)^4+A(4,4);
A(4,5) = x(i,j)^3*y(i,j)+A(4,5);
A(4,6) = x(i,j)^2*y(i,j)^2+A(4,6);
A(5,1) = x(i,j)*y(i,j)+A(5,1);
A(5,2) = x(i,j)^2*y(i,j)+A(5,2);
A(5,3) = x(i,j)^3+A(5,3);
A(5,4) = x(i,j)^3*y(i,j)+A(5,4);
A(5,5) = x(i,j)^2*y(i,j)^2+A(5,5);
A(5,6) = x(i,j)*y(i,j)^3+A(5,6);
A(6,1) = y(i,j)^2+A(6,1);
A(6,2) = x(i,j)*y(i,j)^2+A(6,2);
A(6,3) = y(i,j)^3+A(6,3);
A(6,4) = x(i,j)^2*y(i,j)^2+A(6,4);
A(6,5) = x(i,j)*y(i,j)^3+A(6,5);
A(6,6) = y(i,j)^4+A(6,6);
B(1,1) = z(i,j)+B(1,1);
B(2,1) = z(i,j)*x(i,j);
B(3,1) = z(i,j)*y(i,j);
B(4,1) = z(i,j)*x(i,j)^2;
B(5,1) = z(i,j)*x(i,j)*y(i,j);
B(6,1) = z(i,j)*y(i,j)^2;
end
end
C = inv(A)*B;
a0 = C(1);
a1 = C(2);
a2 = C(3);
a3 = C(4);
a4 = C(5);
a5 = C(6);
源码的基本思想是基于数学方程计算 a0~a5 这6个参数的值,并将这些参数以行向量形式返回。我们观察函数文件,看到两层 for 循环的循环体中有 x(i,j) 这样的参数,这要求传入参数 x 需要是一个 length(x)*length(y) 的矩阵,而我们在实际应用的时候,可能传入参数并不满足这样的矩阵形式,更多的可能是个向量,或者[x,y,z] 这样的矩阵,直接以输入参数代入可能会报“位置 1 的索引超出数组范围(不能超过 1)。”的错误。
2. 解决上述问题
找了个比较简单的办法来解决上述问题。我用的 MATLAB 版本是 2018a ,我们知道有一个拟合工具:
>> cftool
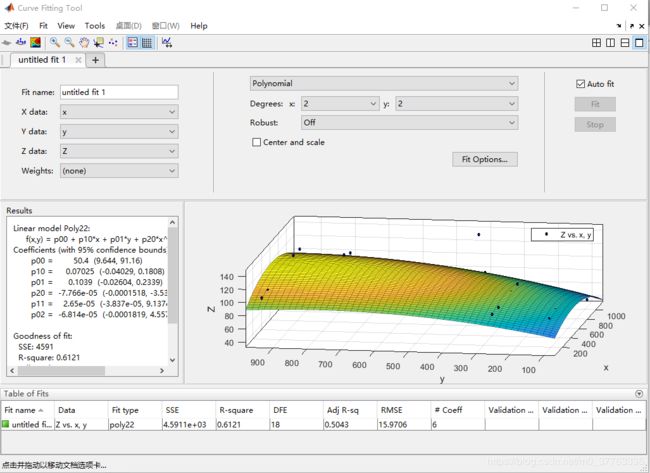
Fit name: 自定义;
x data, y data, z data:都需要从工作空间加载,所以你的这些数据需要先导入到 workspace(工作区);
上部中间的部分是自己设置的参数,第一行 Polynomial 为多项式拟合,拟合算法在类 fittype里面,自己查参数意义;
当然多项式拟合可以选择 x 和 y 的最高次项的幂。
3. 生成源代码
有些同学可能在想:“我要源代码,这样才能往里面传参数啊!!!”
步骤:
文件(File)->Generate Code
它就会自动生成一个函数文件,你直接调用就行了,不过里面还有一些数据类型的问题待解决,也就是函数的返回参数:
[fitresult, gof] = createFit(x, y, Z)

可能你直接用这个做还会遇到有些问题,不过终归不是什么难题了。
还是补充上怎么获取方程系数吧,参考http://www.ilovematlab.com/thread-574266-1-1.html
MATLAB的 coeffvalues()函数。help 文档:“coeffvalues(FUN)返回CFIT对象FUN的系数值作为行向量。”