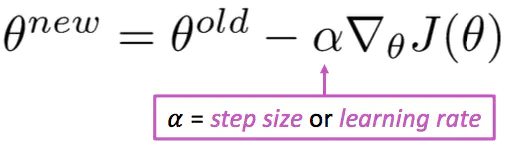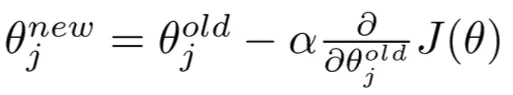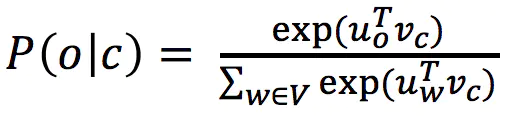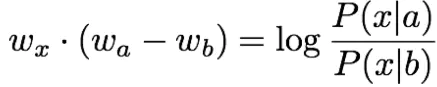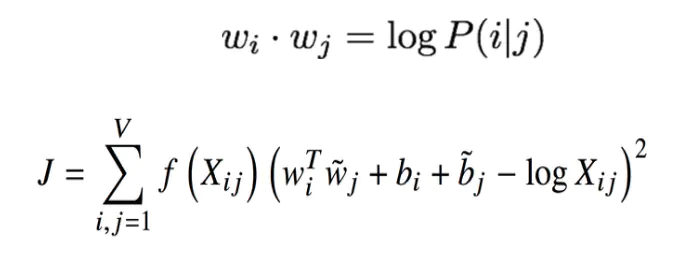Task 2: Word Vectors and Word Senses
1. 复习:word2vec的主要思想
- 遍历整个语料库的每个单词
- 使用单词向量预测周围的单词
更新向量,以便您可以很好地预测
Word2vec参数和计算
每个位置的预测相同
我们希望有一个模型,可以对上下文中出现的所有单词(相当经常)给出合理的高概率估计
Word2vec通过在空间中放置相似的单词来最大化目标函数
2. 优化:梯度下降
- 我们有一个要最小化的成本函数J(θ)
- 梯度下降是最小化J(θ)的算法
- 想法:对于θ的当前值,计算J(θ)的梯度,然后朝负梯度的方向走一小步。 重复。
注意:我们的目标可能不会像这样凸出
梯度下降
- 更新公式(以矩阵表示法):
- 更新公式(对于单个参数):
- 算法:
while True:
theta_grad = evaluate_gradient(J,corpus,theta)
theta = theta - alpha * theta_grad
随机梯度下降
- 问题:J(θ)是语料库中所有窗口的函数(可能是数十亿!)
- 因此∇θJ(θ)的计算非常昂贵
- 您将等待很长时间才能进行单个更新!
- 对于几乎所有的神经网络来说,这都是一个非常糟糕的主意!
- 解决方案:随机梯度下降(SGD)
- 反复采样窗口,并在每个窗口之后进行更新
- 算法:
while True:
window = sample_window(corpus)
theta_grad = evaluate_gradient(J,window,theta)
theta = theta - alpha * theta_grad
单词向量的随机渐变!
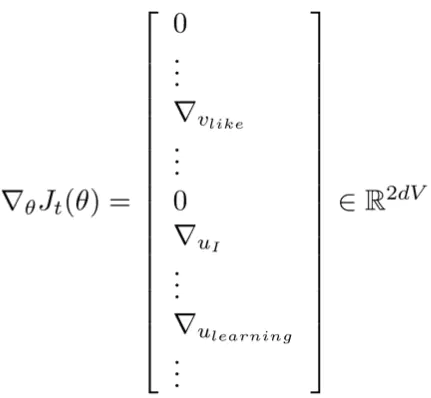
- 在每个这样的窗口迭代获取SGD的梯度
- 但是在每个窗口中,我们最多只有2m +1个字,
所以∇θJt(θ)非常稀疏!
- 我们可能只会更新实际出现的单词向量!
- 解决方案:您需要稀疏矩阵更新操作以仅更新完全嵌入矩阵U和V的某些行,或者您需要保留散列以保留词向量
- 如果您有数百万个单词向量并进行分布式计算,那么不必发送大量更新就很重要!
1b. Word2vec:更多详细信息
为什么选择两个向量?更容易优化。 最后对两者进行平均•每个单词只用一个向量就能做到
两种模型:
1.Skip-grams(SG)
预测给定中心的上下文(“外部”)单词(与位置无关)
字
2.连续词袋(CBOW)
从上下文词袋中预测中心词
我们介绍了:跳过图模型
训练效率更高:
1.负采样
到目前为止:专注于朴素的softmax(简单但昂贵的训练方法)
具有负采样(HW2)的跳过语法模型
- 归一化因子在计算上过于昂贵。
- 因此,在标准word2vec和HW2中,您可以执行负采样的skip-gram模型
- 主要思想:训练一个真实对(中心词和上下文窗口中的词)与几个噪声对(中心词与一个随机词配对)的二进制逻辑回归
- 摘自论文:“单词和短语的分布式表示及其组成”(Mikolov等,2013)
- 总体目标函数(它们最大化):
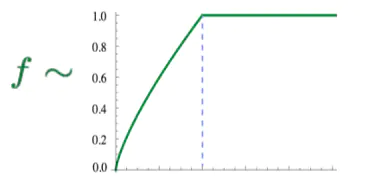
- sigmoid函数(我们很快会成为好朋友):
- 因此,我们在第一对数中最大化了两个单词同时出现的概率
- 表示法更类似于class和HW2:
- 我们取k个否定样本(使用单词概率)
- 最大化出现真实的外部单词的可能性,
最小化概率。 在中心词周围出现随机词 - P(w)= U(w)3/4 / Z,
- 将字母组合分布U(w)提高到3/4幂(我们在入门代码中提供了此功能)。
- 强大的功能使单词词频次降低
3.但是为什么不直接捕获同现计数呢?
与同现矩阵X
- 2个选项:Windows与完整文档
- 窗口:类似于word2vec,在每个单词周围使用窗口-捕获语法(POS)和语义信息
- Word文档共现矩阵将给出导致“潜在语义分析”的一般主题(所有运动术语将具有相似的条目)
示例:基于窗口的共现矩阵
- 窗口长度1(更常见的是5-10)
- 对称(与左或右上下文无关)
- 示例语料库:
- I like deep learning.
- I like NLP.
- I enjoy flying.
| counts | I | like | enjoy | deep | learning | NLP | flying | . |
|---|---|---|---|---|---|---|---|---|
| I | 0 | 2 | 1 | 0 | 0 | 0 | 0 | 0 |
| like | 2 | 0 | 0 | 1 | 0 | 1 | 0 | 0 |
| enjoy | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| deep | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| learning | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| NLP | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| flying | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| . | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 |
简单共现向量的问题
- 词汇量增加
- 尺寸很高:需要大量存储
- 后续分类模型存在稀疏性问题
->模型不那么健壮
解决方案:低维向量
- 想法:将“大多数”重要信息存储在固定的少量维度中:密集的向量
- 通常为25–1000个维度,类似于word2vec。
- 如何降低维度?
方法1:X(HW1)上的降维
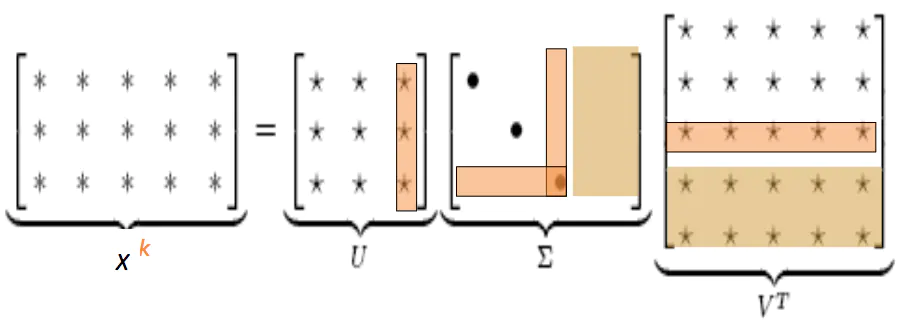
共生矩阵X的奇异值分解将X分解为UΣVT,其中U和V是正交的
为了概括,仅保留k个奇异值。
X^是用最小二乘法表示的X的最佳秩k近似值。经典的线性代数结果。计算大型矩阵的成本很高。
Python中的简单SVD词向量
语料库:
I like deep learning. I like NLP. I enjoy flying.
import numpy as np
la = np.linalg
words = ["I","like","enjoy","deep","learnig","NLP","flying","."]
X = np.array([[0,2,1,0,0,0,0,0],
[2,0,0,1,0,1,0,0],
[1,0,0,0,0,0,1,0],
[0,1,0,0,1,0,0,0],
[0,0,0,1,0,0,0,1],
[0,1,0,0,0,0,0,1],
[0,0,1,0,0,0,0,1],
[0,0,0,0,1,1,1,0]])
U,s,Vh = la.svd(X, full_matrices = False)
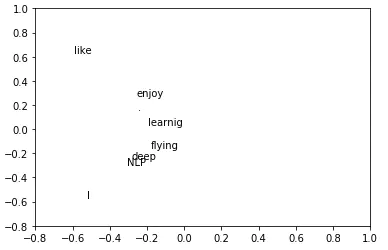
打印对应于2个最大奇异值的U的前两列
import matplotlib.pyplot as plt
plt.ylim(-0.8, 1)
plt.xlim(-0.8, 1)
for i in range(len(words)):
plt.text(U[i,0],U[i,1],words[i])
对X的攻击(在Rohde等人2005中多次使用)
- 缩放单元格中的计数可以有很大帮助
- 问题:功能词(the,he,has)也太频繁的
->语法影响太大。 一些修复:- min(X,t), with t ≈ 100
- 忽略它们
- 倾斜的窗户可以计算出更多的单词
- 使用Pearson相关而不是计数,然后设置负值为0
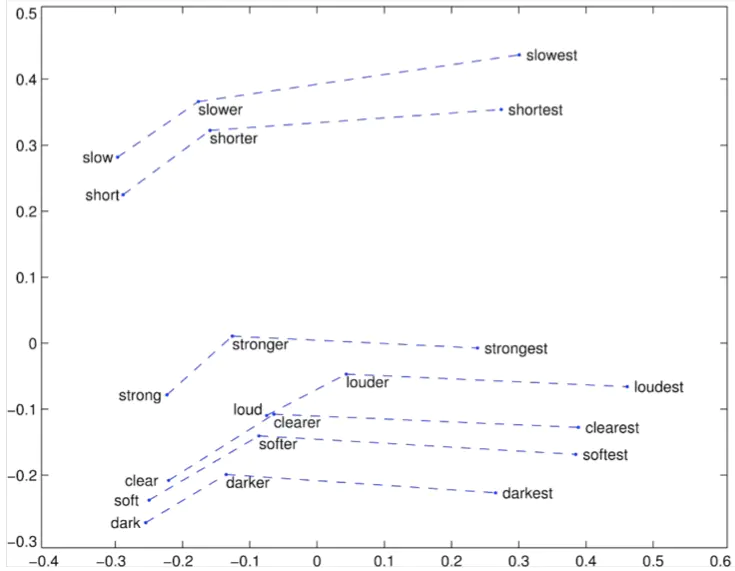
向量中出现有趣的句法模式
来自的COALS模型
一种基于词法共现的语义相似度改进模型。 2005年
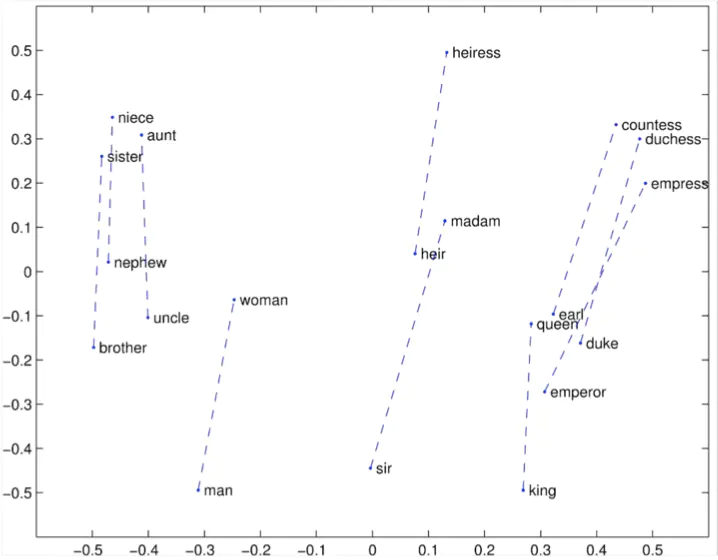
向量中出现有趣的语义模式
来自的COALS模型
基于词法共现的语义相似度改进模型
罗德(Rohde)等人。 2005年
基于计数与直接预测
- LSA,HAL(隆德和伯吉斯),COALS,Hellinger-PCA(Rohdeet al,Lebret和Collobert)
- 快速训练
- 有效利用统计数据
- 主要用于捕获单词相似度
- 不计其数的重要性
- Skip-gram/ CBOW(Mikolov等人)NNLM,HLBL,RNN(Bengio等; Collobert&Weston; Huang等; Mnih&Hinton)
- 具有语料库大小的音阶
- 统计使用率低
- 在其他任务上产生更高的性能
- 可以捕获单词相似度以外的复杂模式
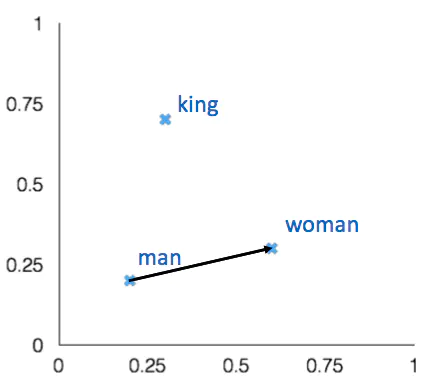
矢量差异中的编码含义
重要启示:
同现概率的比率可以编码含义成分
| x = solid | x = gas | x = water | x = random | |
|---|---|---|---|---|
| P(x!ice | large | small | large | small |
| P(x!steam) | small | large | large | small |
| P(x!ice)/P(x!steam) | large | small | ~1 | ~1 |
| x = solid | x = gas | x = water | x = fashion | |
|---|---|---|---|---|
| P(x!ice | 1.9 x 10 -4 | 6.6 x 10-5 | 3.0 x 10 -3 | 1.7 x 10 -5 |
| P(x!steam) | 2.2 x 10-5 | 7.8 x 10-4 | 2.2 x 10-3 | 1.8 x 10-5 |
| P(x!ice)/P(x!steam) | 8.9 | 8.5 x 10-2 | 1.36 | 0.96 |
问:我们如何捕获单词向量空间中共现概率的比率作为线性含义成分?
答:对数双线性模型:
具有向量差异
融合两全其美的GloVe
- 快速训练
- 可扩展到大型语料库
- 即使具有较小的语料库和较小的向量也表现良好
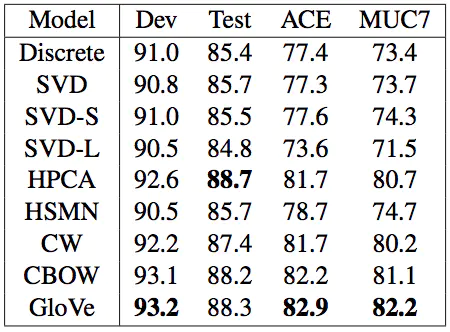
GloVe结果
如何评估词向量?
- 与自然语言处理中的一般评估有关:内部与外部
- 内部:
- 评估特定/中间子任务
- 快速计算
- 帮助了解该系统
- 如果没有建立与实际任务的相关性,则不清楚是否有帮助
- 外在的:
- 评估任务
- 可以始终保证计算准确性
- 不清楚子系统是否存在与其他子系统相互作用的问题
- 如果完全替换一个子系统并进一步提高准确性,那将是一个胜利!
内在词向量评估
- 词向量类比
- 通过添加后的余弦距离捕获直观的语义和句法类比问题来评估单词向量
- 从搜索中丢弃输入的单词!
- 问题:如果信息在那里但不是线性的,该怎么办?
Glove 可视化
Glove 可视化:公司-CEO
Glove 可视化:最高级
内在词向量评估的详细信息
- 词向量类比:http://code.google.com/p/word2vec/source/browse/trunk/questions- words.txt中的句法和语义示例
: city-in-state
Chicago Illinois Houston Texas
Chicago Illinois Philadelphia Pennsylvania Chicago Illinois Phoenix Arizona
Chicago Illinois Dallas Texas
Chicago Illinois Jacksonville Florida Chicago Illinois Indianapolis Indiana Chicago Illinois Austin Texas
Chicago Illinois Detroit Michigan
Chicago Illinois Memphis Tennessee Chicago Illinois Boston Massachusetts
问题:不同城市的名称可能相同
- 词向量类比:下面的句法和语义示例
: gram4-superlative
bad worst big biggest
bad worst bright brightest bad worst cold coldest bad worst cool coolest bad worst dark darkest bad worst easy easiest bad worst fast fastest
bad worst good best
bad worst great greatest
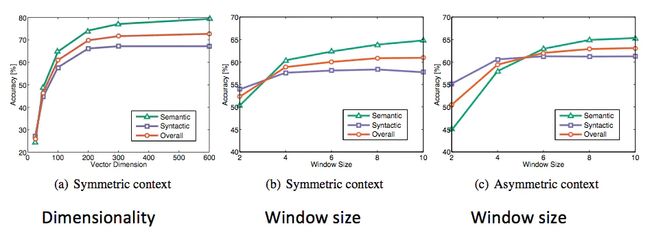
类比评估和超参数
- Glove词向量评估
- 好的尺寸是〜300
- 非对称上下文(仅左侧单词)效果不佳
- 但这对于下游任务可能有所不同!
- 每个中心词周围8的窗口大小适合手套矢量
词嵌入的维数
[Zi Yin and Yuanyuan Shen, NeurIPS 2018]
使用矩阵摄动理论,揭示了词嵌入维数选择中的基本偏差-方差折衷
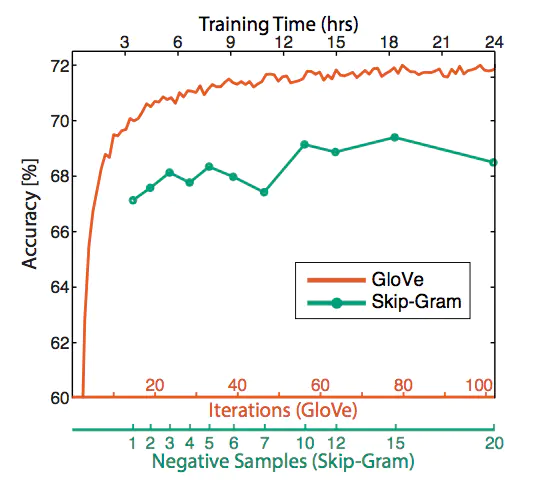
- 更多训练时间有帮助
- 更多数据有帮助,维基百科比新闻文本更好!
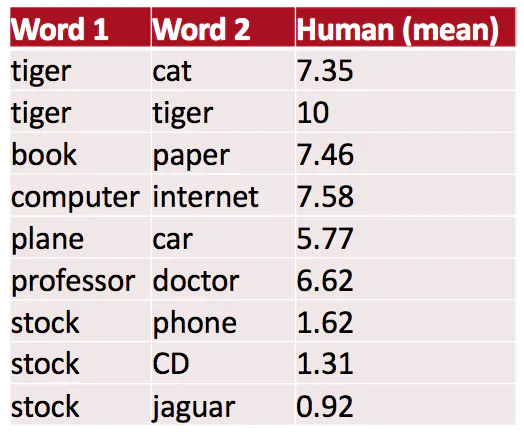
另一个内在词向量评估
- 词向量距离及其与人类判断的相关性
- 示例数据集:WordSim353
http://www.cs.technion.ac.il/~gabr/resources/data/wordsim353/
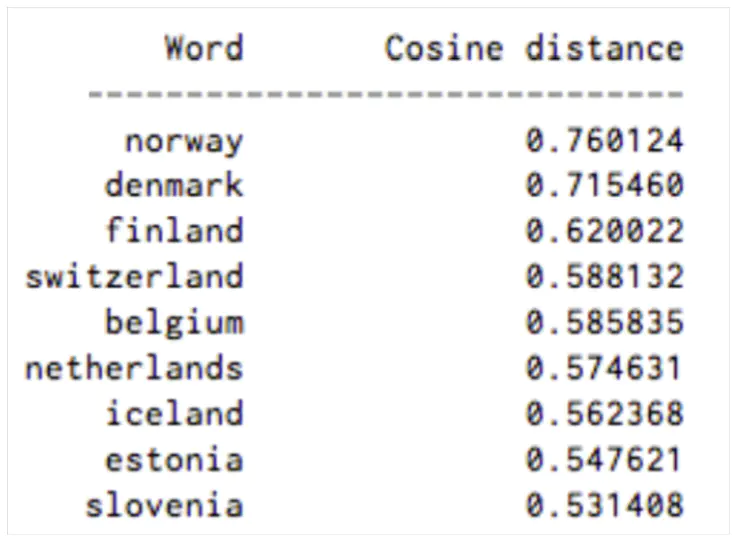
最接近的词“瑞典”(余弦相似度)
相关评估
- 词向量距离及其与人类判断的相关性
- Glove论文中的一些想法也已显示出可以改善skip-gram(SG)模型(例如,将两个向量相加)
词义和词义歧义
-
大多数单词都有很多含义!
-
特别常见的词
-
特别是已存在很久的单词
-
示例:pike
-
一个矢量捕获所有这些含义还是我们一团糟?
pike -
尖锐的人员
-
一种拉长的鱼
-
铁路线或系统
-
道路类型
-
未来(降低收益)
-
一种身体姿势(例如在潜水中)
-
用长矛杀死或刺穿
-
走自己的路(一起走)
-
用澳大利亚英语来说,派克是指退出某件事:我认为他本可以爬上那座悬崖,但他却戳了一下!
通过全局上下文和多种单词原型改进单词表示(Huang等,2012)
- 想法:围绕单词围绕单词窗口,对每个单词进行重新训练,将其分配给多个不同的类bank1,bank2等
词义的线性代数结构及其在多义性中的应用
外在词向量评估
- 词向量的外在评估:此类中的所有后续任务
- 一个好的单词向量应直接帮助的例子:命名实体识别:找到一个人,组织或位置
Reference: https://www.jianshu.com/p/64817a61a958