复习 KMP 算法
KMP 算法是课本上就要求要学的(课本上没 扩展 KMP 和 Manacher ),可见 KMP 有多重要了 。
给定两个字符串 a , b(序列也可以,不一定非得是字符串) , 求第一个串在第二个串中第一次出现的位置,或者出现的次数。
如果暴力做,a 字符串在中途匹配失败,就从头开始,继续匹配,时间复杂度是 O( n * m ) 。
KMP 算法就是一种让主串下标不减小的优化算法,时间复杂度 O( n + m ) , 线性的。
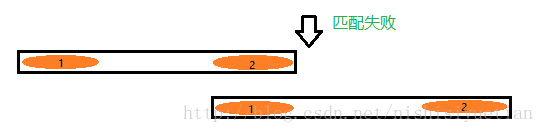
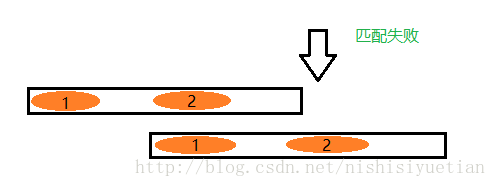
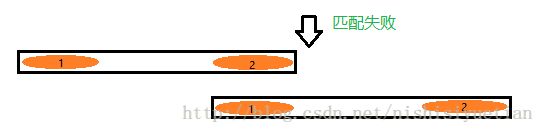
上图中的例子很明显, 匹配失败的时候,直接跳过了一些字符(bcd ),直接到了主串的第二个 ab,而不是让子串 t 从主串的 第二位开始比较
可以说是字符串在匹配失败的时候,直接让最长前缀跳到最长后缀(1 和 2 信息是一模一样的),也就是图中的 1 直接跳到 2 处继续比较,因为 1 和 2 是一样的,可以减少这一段的比较。而且,保证了主串只增不减。
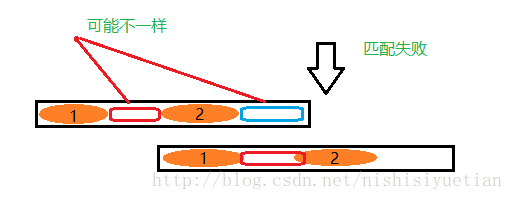
那中间那一块白色的呢? 在一个字符串中要找子串,起始位置的信息一定要和 子串首个字母信息一样吧。假设在白色部分有起始字母一样的部分(前缀)
匹配失败了,能不能像上面那样跳呢?当然是不行的,因为前面的白色和后面的白色不一定一样,
如果跳到其他地方,就更不可能了,因为至少首字母相同或者有最长前缀。
所以,必须是一头一尾,分别有一段相同,这样可以保证 “跳过的已经匹配的部分 ” 是一样的,就是上面的 1
不过都是针对当前匹配到的位置而言的最长前缀(上面的1)和最长后缀(上面的2)。
放到整个子串而言,从起始到每个位置的最长前缀和最长后缀不尽相同。
接下来,就是如何求跳到哪里了。引入一个 Next 数组,如果子串在某处匹配失败,就拿子串当前的最长前缀来“替换”已经匹配的最长后缀 。
求 Next 数组:
设子串为 text , 要做的就是增大最长前缀和最长后缀
void Get_Next(){
int i = 0 , j = -1 ;
Next[0] = -1 ;
while( i < (int)text.size() ){
if( j == -1 || text[j] == text[i] )
Next[++i] = ++j ;
else
j = Next[j] ;
}
}如果突然前缀不等于后缀,不是重新开始,而是拿出前缀的最长前缀 j = Next[j] ,因为前缀匹配失败,前缀的最长前缀也许就和后缀的一部分相同。
(说的再多,不如自己算一遍,算一遍就应该行了......)
模板 Hdu 1711
#include
using namespace std ;
int a[1000005] , b[10005] ;
int Next[10005] ;
int N , M ;
void Get_Next(){ // 求 Next 数组
int i = 0 , j = -1 ;
Next[0] = -1 ;
while( i < M ){
if( j == -1 || b[i] == b[j] )
Next[++i] = ++j ;
else
j = Next[j] ;
}
}
int KMP(){
int i = 0 , j = 0 ;
while( i < N ){
if( j == -1 || a[i] == b[j] )
++i , ++j ;
else
j = Next[j] ;
if( j == M ) // 子串在主串匹配的长度已经恰好是子串的长度的
return i - j + 1 ; // i 是子串的末尾在主串的位置,起始点在 i-j+1 或者 i-M+1
}
return -1 ;
}
int main(){
int cases ;
scanf( "%d" , &cases ) ;
while( cases-- ){
scanf( "%d%d" , &N , &M ) ;
for( int i = 0 ; i < N ; ++i )
scanf( "%d" , &a[i] ) ;
for( int i = 0 ; i < M ; ++i )
scanf( "%d" , &b[i] ) ;
if( N < M ){
printf( "-1\n" ) ; continue ;
}
Get_Next() ;
printf( "%d\n" , KMP() ) ;
}
return 0 ;
} 求 Next 数组还可以优化
相应地,做这个优化是为了减少一些无用的“跳”,因为再次开始比较的字符还是匹配失败的,就再取一次最长前缀。
void Get_Next(){
int i = 0 , j = -1 ;
Next[0] = -1 ;
while( i < M ){
if( j == -1 || b[i] == b[j] ){
++i , ++j ;
Next[i] = b[i] == b[j] ? Next[j] : j ;
}
else
j = Next[j] ;
}
}如果要求子串在主串中出现了多少次,
int KMP(){
int i = 0 , j = 0 , ans = 0 ;
Get_Next() ;
while( i < (int)str.size() && j < (int)text.size() ){
if( j == -1 || text[j] == str[i] ){
i++ ;
j++ ;
}
else
j = Next[j] ;
if( j == (int)text.size() )
ans++ , j = Next[j] ;
}
return ans ;
}