图论--最短路径问题--Dijkstra算法和Floyd算法
最短路径之
(一)简单了解:
用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止。Dijkstra算法能得出最短路径的最优解,但由于它遍历计算的节点很多,所以效率低。
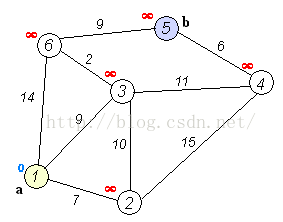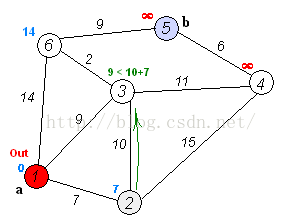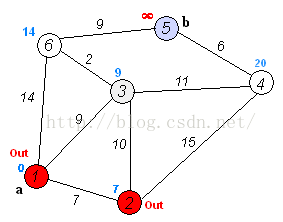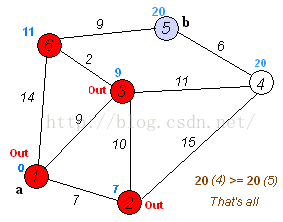
如上图,是求a到b的最短路径,这里并不限定b节点,修改为到任意节点的路径,问题是完全一样的。
首先需要记录每个点到原点的距离,这个距离会在每一轮遍历的过程中刷新。每一个节点到原点的最短路径是其上一
个节点(前驱节点)到原点的最短路径加上前驱节点到该节点的距离。以这个原则,经过N轮计算就能得到每一个
节点的最短距离。
第一轮,可以计算出,2、3、4、5、6到原点1的距离分别为:[7, 9, -1, -1, 14]。-1表示无穷大。取其中最小的,
为7,即可以确定1的最短路径为0,2为下一轮的前驱节点。同时确定2节点的最短路径为7,路线:1->2。
第二轮,取2节点为前驱节点,按照前驱节点的最短距离加上该节点与前驱节点的距离计算新的最短距离,可以得
到3,4,5,6节点到原点的距离为:[17, 22, -1, -1],此时需要将这一轮得到的结果与上一轮的比较,
3节点:17 > 9,最短路径仍然为9;4节点:22 < 无穷大,刷新4节点的最短路径为22;5节点:不变,仍然为无穷
大;6节点:14 < 无穷大,取14,不变。则可以得到本轮的最短距离为:[9, 22, -1, 14],取最短路径最小的节点,
为3,作为下一轮的前驱节点。同时确定3节点的最短路径为9,路线:1->3。
第三轮,同上,以3为前驱节点,得到4,5,6的计算距离为:[20, -1, 11],按照取最短路径的原则,与上一轮的进
行比较,刷新为:[20, –1, 11],选定6为下一轮的前驱节点。同时取定6的最短路径为11,路线:1->3->6。
第四轮,同上,以6为前驱节点,得到4和5的计算距离为[20, 20],与上一轮进行比较,刷新后为[20, 20],二者相等
只剩下两个节点,并且二者想等,剩下的计算已经不需要了。则两个节点的最短路径都为20。整个计算结束。4的
最短路径为20,路线:1->3->4。5的最短路径为20,路线:1->3->6->5。
如果二者不相等,则还需要进行第五轮,先确定二者中的一个的最短路径和路线,再取定剩下的。直到整个5次循
环都完成。
(③)dijkstra算法的流程图如下所示:
(④)Dijkstra算法的执行步骤:
1.先初始化D[i]=v与i之间的距离(若两点不相连则为INIFY),mark[i]=0,p[i]=0,并将起始节点v的mark[v]=0;
2.遍历剩余的节点,找出剩余节点与v之间的距离(初始状态下除去相连的节点间有距离外其余所有节点间距离为INIFY),不相连的节点依然设为INIFY不变。找出其中与v距离最小的那个点k,mark[k]=1;
3.遍历所有节点,对其中mark[i]==0的点与k点的距离+2中的那个最小距离与D[i]比较,若小于D[i]则更新D[i],并将p[i]标记为k(k为该节点的前驱)。
4.遍历完后得到的D[i]就是v到各个节点的最短距离.
//初始化v[0]到v[i]的距离
for(int i=1;i<=n;i++)
dis[i] = w[0][i];
vis[0]=1;//标记v[0]点
for(int i = 1; i <= n; i++)
{
//查找最近点
int min = INF,k = 0;
for(int j = 0; j <= n; j++)
if(!vis[w] && dis[j] < min)
min = dis[w],k = j;
vis[k] = 1;//标记查找到的最近点
//判断是直接v[0]连接v[j]短,还是经过v[k]连接v[j]更短
for(int j = 1; j <= n; j++)
if(!vis[j] && min+w[k][j] < dis[j])
d[j] = min+w[k][j];
}
return dis[j];
}
测试数据 教科书 P189 G6 的邻接矩阵 其中 数字 1000000 代表无穷大
6
1000000 1000000 10 100000 30 100
1000000 1000000 5 1000000 1000000 1000000
1000000 1000000 1000000 50 1000000 1000000
1000000 1000000 1000000 1000000 1000000 10
1000000 1000000 1000000 20 1000000 60
1000000 1000000 1000000 1000000 1000000 1000000
结果:
D[0] D[1] D[2] D[3] D[4] D[5]
0 1000000 10 50 30 60
#include
#include
#define MAX 1000000
using namespace std;
int arcs[10][10];//邻接矩阵
int D[10];//保存最短路径长度
int p[10][10];//路径
int final[10];//若final[i] = 1则说明 顶点vi已在集合S中
int n = 0;//顶点个数
int v0 = 0;//源点
int v,w;
void ShortestPath_DIJ()
{
for (v = 0; v < n; v++) //循环 初始化
{
final[v] = 0; D[v] = arcs[v0][v];
for (w = 0; w < n; w++)
if (D[v] < MAX) {p[v][v0] = 1; p[v][v] = 1;}
}
D[v0] = 0; final[v0]=0; //初始化 v0顶点属于集合S
//开始主循环 每次求得v0到某个顶点v的最短路径 并加v到集合S中
for (int i = 1; i < n; i++)
{
int min = MAX;
for (w = 0; w < n; w++)
{
//我认为的核心过程--选点
if (!final[w]) //如果w顶点在V-S中
{
//这个过程最终选出的点 应该是选出当前V-S中与S有关联边
//且权值最小的顶点 书上描述为 当前离V0最近的点
if (D[w] < min) {v = w; min = D[w];}
}
}
final[v] = 1; //选出该点后加入到合集S中
for (w = 0; w < n; w++)//更新当前最短路径和距离
{
/*在此循环中 v为当前刚选入集合S中的点
则以点V为中间点 考察 d0v+dvw 是否小于 D[w] 如果小于 则更新
比如加进点 3 则若要考察 D[5] 是否要更新 就 判断 d(v0-v3) + d(v3-v5) 的和是否小于D[5]
*/
if (!final[w] && (min+arcs[v][w]
D[w] = min + arcs[v][w];
// p[w] = p[v];
p[w][w] = 1; //p[w] = p[v] + [w]
}
}
}
}
int main()
{
cin >> n;
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
cin >> arcs[i][j];
}
}
ShortestPath_DIJ();
for (int i = 0; i < n; i++) printf("D[%d] = %d\n",i,D[i]);
return 0;
}
题目大意:
搬东西很累,想省力,给你几个点和点之间的距离;标准题型;
输入:包括多组数据。每组数据第一行是两个整数N、M(N<=100,M<=10000),N表示成都的大街上有几个路口,标号为1的路口是商店所在地,标号为N的路口是赛场所在地,M则表示在成都有几条路。N=M=0表示输入结束。接下来M行,每行包括3个整数A,B,C(1<=A,B<=N,1<=C<=1000),表示在路口A与路口B之间有一条路,我们的工作人员需要C分钟的时间走过这条路。输入保证至少存在1条商店到赛场的路线。
#include
using namespace std;
#define INF 0xfffffff
int maps[110][110],dis[110],visit[110];//maps[1][2]=10为点1到点2的值为10;visit[1]=1 为1这个点已经处理
int n,m;//n为多少个路口也就是多少个点,m为多少条路也就是多少个相互连接的点
int dijstra()
{
memset(visit,0,sizeof(visit));//初始化visit的所有的值
for (int i=1;i<=n;i++)
{
dis[i]=maps[1][i];//将1点到其他所有点的值赋给dis[i];
}
visit[1]=1;//标记1点已经处理
dis[1]=0;//到自己的距离为0
for (int i=1;i<=n;i++)
{
int pos;//记录j值;
int mins=INF;//记录最小值
for (int j=1;j<=n;j++)
{
if (!visit[j]&&mins>dis[j])//j点未被处理,且j点到1点的值最小
{
pos=j;//记住j这个点
mins=dis[j];//更新最小值
}
}
visit[pos]=1;//已经处理pos这个点;
for (int j=1;j<=n;j++)
{
if (!visit[j]&&dis[j]>dis[pos]+maps[pos][j])//循环不断找出结点;
{
dis[j]=dis[pos]+maps[pos][j];
}
}
}
return dis[n];//终点在n这个地方;
}
int main()
{
int i,j;
while(~scanf("%d%d",&n,&m),n||m)
{
for(i=1;i<=n;++i)
{
for(j=1;j<=n;++j)
{
maps[i][j]=INF;
}
}
int a,b,c;//a,b都为两个相互连接的点,c为连接的距离
for(i=1;i<=m;++i)
{
scanf("%d%d%d",&a,&b,&c);
if(c
}
int counts=dijstra();
printf("%d\n",counts);
}
return 0;
}
第二行有徐总的所在地start,他的目的地end;
接着有n行,每行有站名s,站名e,以及从s到e的时间整数t(0
如果N==-1,表示输入结束。
Sample Input
6
xiasha westlake
xiasha station 60
xiasha ShoppingCenterofHangZhou 30
station westlake 20
ShoppingCenterofHangZhou supermarket 10
xiasha supermarket 50
supermarket westlake 10
-1
Sample Output
50
#include
#include
#include
#define INF 0x3ffffff
#define MAXs 170
using namespace std;
int dis[MAXs],visit[MAXs],maps[MAXs][MAXs];
char s[35],e[35],place[MAXs][35];
int counts;
void Dijkstra(int start,int endd)
{
//int pos=start;
memset(visit,0,sizeof(visit));
for(int i=1;i<=counts;i++)
dis[i]=maps[start][i];
visit[start]=1;
dis[start]=0;
for(int i=1;i<=counts;i++)
{
int mins=INF;
int pos;
for(int j=1;j<=counts;j++)
if(!visit[j]&&mins>dis[j])
{
mins=dis[j];
pos=j;
}
visit[pos]=1;
for(int j=1;j<=counts;j++)
if(!visit[j]&&dis[j]>dis[pos]+maps[pos][j])
dis[j]=dis[pos]+maps[pos][j];
}
if(dis[endd]==INF)
printf("-1\n");
else
printf("%d\n",dis[endd]);
}
int main()
{
int N;
int a,b,sign,leng;
while(~scanf("%d",&N)&&N!=-1)
{
for(int i=1;i
if(i==j)
maps[i][j]=0;
else
maps[i][j]=INF;
}
scanf("%s%s",place[1],place[2]);//起始点
counts=2;
while(N--)
{
int leng;//两点的距离
scanf("%s%s%d",s,e,&leng);//输入并提示两点及距离
sign=0;//相当于标记变量
for(int i=1;i<=counts;i++)
if(strcmp(s,place[i])==0)//查找是否记录到数组中
{
sign=1;
a=i;//记录匹配到的位置;
break;
}
if(!sign)
{
counts++;
strcpy(place[counts],s);
a=counts;
//若没有记录入数组,则加入数组,其字符串地名对应的编号即为数组的下标,当前的counts值
}
//重复操作对比站点e
sign=0;//需要更新sign的值
for(int i=1;i<=counts;i++)
if(strcmp(e,place[i])==0)
{
sign=1;
b=i;
break;
}
if(!sign)
{
counts++;
strcpy(place[counts],e);
b=counts;
}
if(maps[a][b]>leng)
maps[a][b]=maps[b][a]=leng;
}
if(strcmp(place[1],place[2])==0)
printf("0\n");
else
Dijkstra(1,2);
}
return 0;
}
#include
#include
#include
#include
#include
#include
#include
#include
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
if(maps[i][k]!=INF&&maps[k][j]!=INF)
maps[i][j]=min(maps[i][k]+maps[k][j],maps[i][j]);
//Floyd算法模板
其他的地方和上边的算法差不多,。多多理解。
算法思想原理:
Floyd算法是一个经典的动态规划算法,稠密图效果最佳,边权可正可负。此算法简单有效,由于三重循环结构紧凑,对于稠密图,效率要高于执行|V|次Dijkstra算法,也要高于执行|V|次SPFA算法。用通俗的语言来描述的话,首先我们的目标是寻找从点i到点j的最短路径。从动态规划的角度看问题,我们需要为这个目标重新做一个诠释(这个诠释正是动态规划最富创造力的精华所在)
从任意节点i到任意节点j的最短路径不外乎2种可能,1是直接从i到j,2是从i经过若干个节点k到j。所以,我们假设Dis(i,j)为节点u到节点v的最短路径的距离,对于每一个节点k,我们检查Dis(i,k) + Dis(k,j) < Dis(i,j)是否成立,如果成立,证明从i到k再到j的路径比i直接到j的路径短,我们便设置Dis(i,j) = Dis(i,k) + Dis(k,j),这样一来,当我们遍历完所有节点k,Dis(i,j)中记录的便是i到j的最短路径的距离。
算法描述:
a.从任意一条单边路径开始。所有两点之间的距离是边的权,如果两点之间没有边相连,则权为无穷大。
b.对于每一对顶点 u 和 v,看看是否存在一个顶点 w 使得从 u 到 w 再到 v 比己知的路径更短。如果是更新它。
②:基本代码
很简单吧,代码看起来可能像下面这样:
但是这里我们要注意循环的嵌套顺序,如果把检查所有节点X放在最内层,那么结果将是不正确的,为什么呢?因为这样便过早的把i到j的最短路径确定下来了,而当后面存在更短的路径时,已经不再会更新了。
让我们来看一个例子,看下图:
图中红色的数字代表边的权重。如果我们在最内层检查所有节点X,那么对于A->B,我们只能发现一条路径,就是A->B,路径距离为9。而这显然是不正确的,真实的最短路径是A->D->C->B,路径距离为6。造成错误的原因就是我们把检查所有节点X放在最内层,造成过早的把A到B的最短路径确定下来了,当确定A->B的最短路径时Dis(AC)尚未被计算。所以,我们需要改写循环顺序,如下:
毕竟这个算法比较简单加上上边也有有关例题,所以再找一个简单的例题!!
poj 3615 Cow Hurdles
题意:
给你一个有向图,然后对于特定的点A与B,要你求出A到B之间所有可行路径的单段路距离最大值的最小值.(有点绕)
分析:
剥除floyd的外壳,本题d[i][j]表示的是从i到j的所有路径中单段路距离最大值的最小值。所以其实本题还是依据动态规划的思想来做的,
当不同类d[i][k]和d[k][j]合并的时候,取得是max(最大值,因为我们要求i到j这段路内的最大值)。然后当同类路径值(即两个d[i][j]可行值)选优时,取得是最小值(因为我们要求所有i到j路径目的值中的最小值)。
代码:
#include
#include
#define INF 1e9
using namespace std;
const int maxn = 300+10;
int n,m,t;
int d[maxn][maxn];
void floyd()
{
for(int k=1;k<=n;k++)
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
if(d[i][k]
}
int main()
{
while(scanf("%d%d%d",&n,&m,&t)==3)
{
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
d[i][j]= i==j?0:INF;
for(int i=1;i<=m;i++)
{
int u,v,height;
scanf("%d%d%d",&u,&v,&height);
d[u][v]=height;
}
floyd();
while(t--)
{
int u,v;
scanf("%d%d",&u,&v);
printf("%d\n",d[u][v]==INF?-1:d[u][v]);
}
}
return 0;
}