Mnist手写数字识别之CNN实现

Mnist手写数字识别之CNN实现

最近有点闲，想整一下机器学习，本以为自己编程还不错，想想机器学习也不难，结果被自己啪啪啪的打脸，还疼的不行。

废话不多说，开始搞事情。

本博客的主要内容是：通过TF一步一步用卷积神经网络（CNN）实现手写Mnist数字识别

如果你很牛逼，就不用看我哔哔了，我菜鸟一只，本博客中涉及到多个方面的知识，有的是引用其他博客的知识，会给出相应的连接，我就做一个知识的整理者。（ps：应该没有人整理的有我这么清楚明了吧。）

实验环境：本代码是在win10系统上运行得出的结果，python版本3.6，其他相关的依赖库和文件均为2019/1/10截止前最新版本。

目录结构：

• 一、TF相关函数的使用介绍；
• 二、CNN网络模型以及相关实现；
• 三、运行结果展示；
• 四、Tensor图；
• 五、代码实现。

一、TF相关函数使用介绍：

注：下面相关函数的解释均来自TF的官方文档，配套中文翻译带示例。

1.tf.reshape()

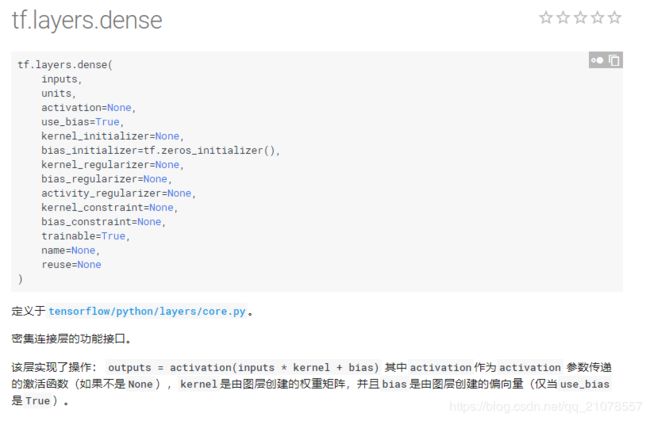
2. tf.layers.conv2d()
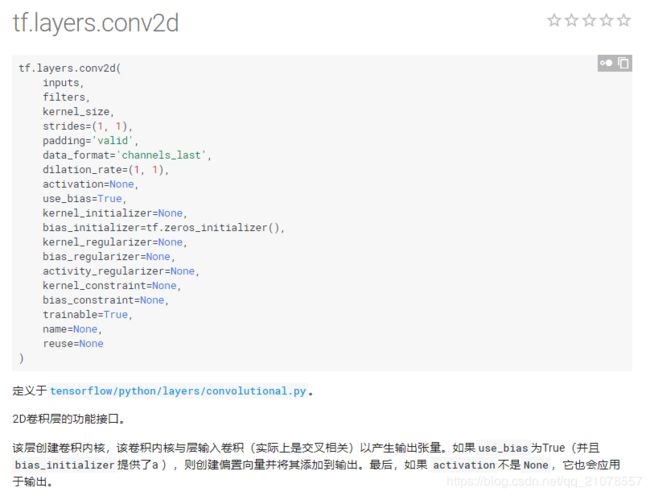
注：此函数实际上是卷积层函数，对张量进行卷积，此函数对应的是CNN中的卷积层。具体的参数如下：

3. tf.layers.max_pooling2d()
注：此函数的输入是经过 tf.layers.conv2d() 卷积后的张量，此函数对应的是CNN中的池化层。

4.tf.layers.dense()

5. tf.layers.dropout()

6. tf.losses.softmax_cross_entropy()

7. tf.metrics.accuracy()

二、CNN网络模型以及相关实现

首先在开始CNN之前，请把这张图死记硬背记住，因为所有的一切都是围绕着这张图来实现的。

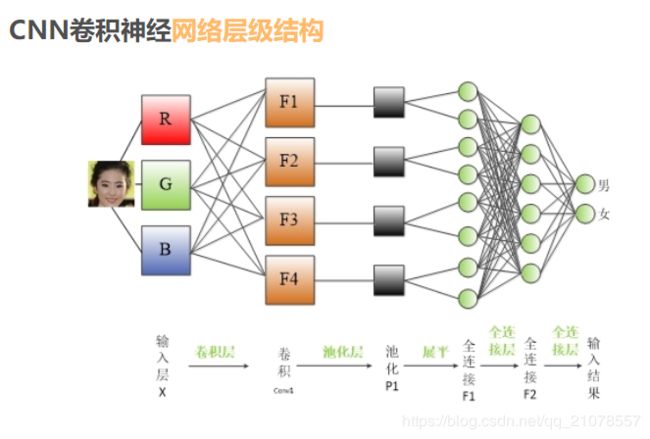
接下来就是你需要自己去看着三篇博客的内容：很重要对后续的代码理解，而且图文并茂，生动形象，逼真到你不要不要的。按照这个顺序看，容易理解一些。

1、深入学习卷积神经网络中卷积层和池化层的意义

2、卷积神经网络（一）——卷积、边缘化与池化层

3、卷积神经网络中卷积、反卷积、池化解析

三、运行结果展示

此结果是训练了5000次后的模型，准确率还是蛮高的。最后从测试数据集中选取位置在20的图像进行测试。

从上图可以看出，采用Relu这个激活函数，刚开始的时候收敛速度非常快，经过几百步的训练就可以得到相对于比较高的识别率了。

最后的运行结果如下所示，都预测正确了，准确率达到了96%，你要是有强迫症，你可以训练20000次，估计正确率能达到98左右，但是前提是你的电脑要牛掰，不然就是漫长的等待：

四、Tensor图

五、代码实现

下面的代码写的很详细，每一步是干啥的都写了，结合上面所说的知识，理解应该不是很难

# -*- coding: UTF-8 -*-
import numpy as np
import tensorflow as tf

# down load and load Mnist library(55000 * 28 * 28)
from tensorflow.examples.tutorials.mnist import input_data

mnist = input_data.read_data_sets('mnist_data', one_hot=True)

# 代表训练数据, /255. 的目的是其取值范围在【0,255】
input_x = tf.placeholder(tf.float32, [None, 28 * 28]) / 255.

# 代表的是10个标签，0,1,2,3....9
output_y = tf.placeholder(tf.int32, [None, 10])

# shape 前面使用-1,能够自动的对其形状进行推导
input_x_image = tf.reshape(input_x, [-1, 28, 28, 1])

# 从测试数据集中选取3000个测试数据进行验证模型,
# 每次都使用这一批相同的测试数据进行测试,能够保证唯一性
test_x = mnist.test.images[:3000]  # picture
test_y = mnist.test.labels[:3000]  # label

# 创建 CNN 模型
# 构建第一层 CNN 模型,卷积层
cover1 = tf.layers.conv2d(
	inputs=input_x_image,  # shape is [28, 28, 1]
	filters=32,            # 设置卷积深度为32,意思也就是说有32个卷积核
	kernel_size=[5, 5],    # 设置卷积核的大小
	strides=1,             # 设置卷积的步长
	padding="same",        # 进行卷积后,大小不变
	activation=tf.nn.relu  # 使用 Relu 这个激活函数
)   # [28, 28, 32]

# 构建第一层池化层,作用是对第一层卷积后的结果进行降维,获得池化大小区域内的单个数据进行填充
pool1 = tf.layers.max_pooling2d(
	inputs=cover1,          # shape [28,28,32]
	pool_size=[2, 2],       # 设置池化层的大小
	strides=2               # 设置池化层的步长
)    # shape [14, 14, 32]

# 构建第二层 CNN 模型,卷积层
cover2 = tf.layers.conv2d(
	inputs=pool1,          # shape is [14, 14, 32]
	filters=64,            # 采用64个卷积核
	kernel_size=[5, 5],    # 设置卷积核的大小
	strides=1,             # 设置卷积的步长
	padding="same",        # 进行卷积后,大小不变
	activation=tf.nn.relu  # 使用 Relu 这个激活函数
)   # shape [14, 14, 64]

# 构建第二层池化层,作用是对第二层卷积后的结果进行降维,获得池化大小区域内的单个数据进行填充
pool2 = tf.layers.max_pooling2d(
	inputs=cover2,          # shape [14,14,64]
	pool_size=[2, 2],       # 设置池化层的大小
	strides=2               # 设置池化层的步长
)    # shape [7, 7, 64]

# 展开第二层池化后的数据,使得其维度为一维数组
flat = tf.reshape(pool2, [-1, 7 * 7 * 64])  # shape [7*7*64]

# 设置全连接层网络,共有 1024 个神经元,并且采用Relu这个激活函数
dense = tf.layers.dense(inputs=flat, units=1024, activation=tf.nn.relu)

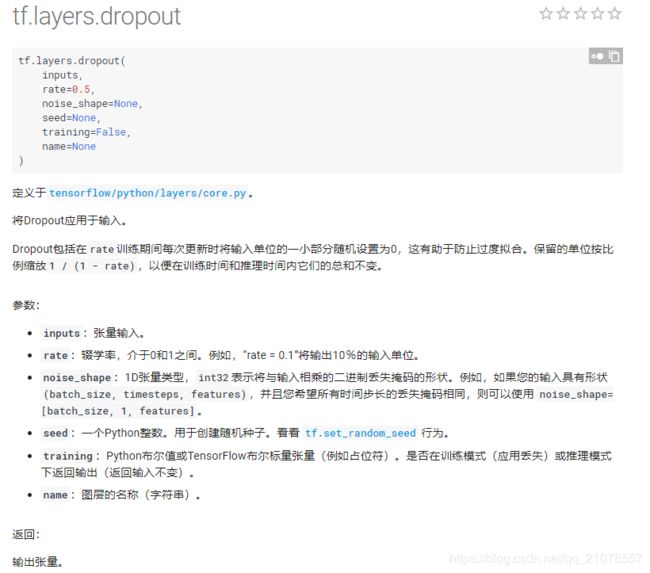
# 为了避免1024个全连接网络神经元出现过拟合,采用Dropout丢弃掉一半的连接,即rate = 0.5
dropout = tf.layers.dropout(inputs=dense, rate=0.5, training=True)

# 定义最后输出10个节点,因为是0-9的数字,一共10个
logites = tf.layers.dense(inputs=dropout, units=10)  # shape [1*1*10]

# 通过使用 softmax 对所有的预测结果和正确结果进行比较并计算概率,
# 然后再使用交叉熵计算概率密度误差,也就是我们的损失函数
loss = tf.losses.softmax_cross_entropy(onehot_labels=output_y, logits=logites)

# 采用 Adam 优化器去优化误差,设置学习率为0.001,能够更好的进行优化
train_op = tf.train.AdamOptimizer(learning_rate=0.001).minimize(loss)

# 计算正确率,正确率的计算步骤:
# 1、对所有的待检测数据进行识别并与正确的结果进行判断,返回bool类型;
# 2、将所有的bool结果进行float操作然后求均值,这个均值就是正确率;
# tf.metrics.accuracy() will return (accuracy,update_op)
accuracy = tf.metrics.accuracy(
	labels=tf.argmax(output_y, axis=1),  # 正确的数字(label)
	predictions=tf.argmax(logites, axis=1)  # 预测的数字(label)
)[1]

with tf.Session() as sess:
	# 初始化局部和全局变量
	init = tf.group(tf.global_variables_initializer(), tf.local_variables_initializer())
	sess.run(init)

	# 保存tensor图
	tf.summary.FileWriter('./log', sess.graph)

	# 定义一共训练10000次
	for i in range(5000):
		# 每次的数据从mnist训练数据集中选取 50 份出来训练
		batch = mnist.train.next_batch(50)  # get 50 sample

		train_loss, train_op_ = sess.run([loss, train_op], {input_x: batch[0], output_y: batch[1]})

		# 每训练100次打印一次训练模型的识别率
		if i % 100 == 0:
			test_accuracy = sess.run(accuracy, {input_x: test_x, output_y: test_y})
			print('Step=%d, Train loss=%.6f, [Test accuracy=%.6f]' % (i, train_loss, test_accuracy))
	
	# 最后一次测试:从测试数据集中选取前 20 张图片进行识别
	# 1.利用现在的模型进行预测数字,test_output 形状是[20,10]
	test_output = sess.run(logites, {input_x: test_x[:20]})
	# 2.获取最大可能性的数字,一维直接返回具体值,二维以上返回下标索引
	inferenced = np.argmax(test_output, 1)
	# 3.打印预测的数字和实际对应的数字
	print('inferenced number:')
	print(inferenced)
	print('Real number:')
	print(np.argmax(test_y[:20], 1))

最后你运行可能需要mnist这个数据集，你自己去百度或者官网下载下来，解压一下就可以。最后附上我的工程结构图。