leetcode52／剑指offer38拓展.N皇后 II 、leetcode51.N皇后、leetcode46／剑指offer38.全排列

题目一：N皇后 II 

1.题目描述

n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

上图为 8 皇后问题的一种解法。

给定一个整数 n，返回 n 皇后不同的解决方案的数量。

示例:

输入: 4
输出: 2
解释: 4 皇后问题存在如下两个不同的解法。
[
 [".Q..",  // 解法 1
  "...Q",
  "Q...",
  "..Q."],

 ["..Q.",  // 解法 2
  "Q...",
  "...Q",
  ".Q.."]
]

2.解题思路

剑指offer上解决八皇后问题，没有用传统的递归或非递归回溯法，而是用了很巧妙的全排列法。

    先说下八皇后问题：在8 X 8的国际象棋上摆放八个皇后，使其不能相互攻击，即任意两个皇后不得处于同一行，同一列或者同意对角线上，求出所有符合条件的摆法。

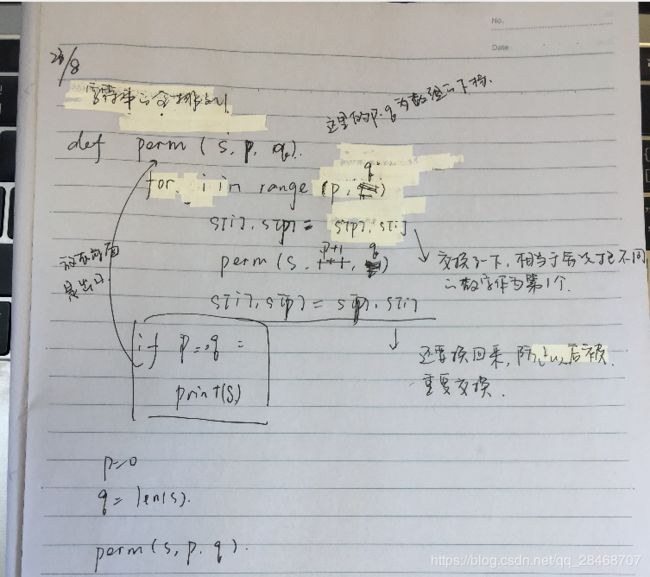
    全排列解决八皇后问题的思路如下：

    由于8个皇后不能处在同一行，那么肯定每个皇后占据一行，这样可以定义一个数组A[8]，数组中第i个数字，即A[i]表示位于第i行的皇后的列号。先把数组A[8]分别用0-7初始化，接下来对该数组做全排列，由于我们用0-7这7个不同的数字初始化数组，因此任意两个皇后肯定也不同列，那么我们只需要判断每个排列对应的8个皇后中是否有任意两个在同一对角线上即可，即对于数组的两个下标i和j，如果i-j==A[i]-A[j]或i-j==A[j]-A[i]，则认为有两个元素位于了同一个对角线上，则该排列不符合条件。
————————————————
原文链接：https://blog.csdn.net/ns_code/article/details/26614999

3.代码实现

class Solution(object):
    def dfs(self, A, n, begin, res):
        if begin == n:
            for i in range(n):
                for j in range(i+1,n):
                    if i-j==A[i]-A[j] or i-j==A[j]-A[i]:
                        return

            res[0] += 1
            return
        for i in range(begin, n):
            A[begin],A[i] = A[i],A[begin]
            self.dfs(A, n, begin+1, res)
            A[begin],A[i] = A[i],A[begin]

    def totalNQueens(self, n):
        """
        :type n: int
        :rtype: int
        """
        A = [i for i in range(n)]
        res = [0]
        self.dfs(A, n, 0, res)
        return res[0]

题目二：N皇后

1.题目描述

n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

上图为 8 皇后问题的一种解法。

给定一个整数 n，返回所有不同的 n 皇后问题的解决方案。

每一种解法包含一个明确的 n 皇后问题的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

示例:

输入: 4
输出: [
 [".Q..",  // 解法 1
  "...Q",
  "Q...",
  "..Q."],

 ["..Q.",  // 解法 2
  "Q...",
  "...Q",
  ".Q.."]
]
解释: 4 皇后问题存在两个不同的解法。

 

2.解题思路

同上

3.代码实现

class Solution(object):
    def dfs(self, A, n, begin, res):
        if begin == n:
            for i in range(n):
                for j in range(i+1,n):
                    if i-j==A[i]-A[j] or i-j==A[j]-A[i]:
                        return

            tmp = []
            for i in range(n):
                string = "." * A[i] + "Q" + "." * (n-A[i]-1)
                tmp.append(string)
            res.append(tmp)
            return
        for i in range(begin, n):
            A[begin],A[i] = A[i],A[begin]
            self.dfs(A, n, begin+1, res)
            A[begin],A[i] = A[i],A[begin]

    def solveNQueens(self, n):
        """
        :type n: int
        :rtype: List[List[str]]
        """
        A = [i for i in range(n)]
        res = []
        self.dfs(A, n, 0, res)
        return res
    

题目三：leetcode46.全排列

1.题目描述

给定一个没有重复数字的序列，返回其所有可能的全排列。

示例:

输入: [1,2,3]
输出:
[
  [1,2,3],
  [1,3,2],
  [2,1,3],
  [2,3,1],
  [3,1,2],
  [3,2,1]
]

2.解题思路

https://www.bilibili.com/video/av9830088?from=search&seid=11774514993439300933

 

注意如果希望把结果加在list里面，list.append(s)添加进去的始终是同一个s，准确的说，始终是同一块地址，而这个info内容在不停的修改。

所以：list.append(s[:])

3.代码实现

class Solution(object):
    def dfs(self,begin,nums,res):
        if begin == len(nums):
            # 千万不要忘记加入的是[:]
            res.append(nums[:])
            return
        for i in range(begin,len(nums)):
            nums[i],nums[begin] = nums[begin],nums[i]
            self.dfs(begin+1,nums,res)
            nums[i],nums[begin] = nums[begin],nums[i]

    def permute(self, nums):
        """
        :type nums: List[int]
        :rtype: List[List[int]]
        """
        res = []
        self.dfs(0,nums,res)
        return res
"""
输出顺序：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,2,1],[3,1,2]]
"""

调用库函数

def permute(self, nums: List[int]) -> List[List[int]]:
        return list(itertools.permutations(nums))