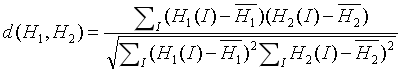OpenCV3学习（8.2）直方图相似度比较compareHist函数与EMD距离

     对输入的两张图像进行直方图均衡化及直方图计算步骤后，可以对两个图像的直方图进行对比，两张图像的直方图反映了该图像像素的分布情况，可以利用图像的直方图，来分析两张图像的关系。

        如果我们有两张图像，并且这两张图像的直方图一样，或者有极高的相似度，那么在一定程度上，我们可以认为这两幅图是一样的，这就是直方图比较的应用之一。   

直方图比较原理

        要比较两个直方图（H1 和 H2），首先必须要选择一个衡量直方图相似度的对比标准，我们设为d(H1,H2)，对输入的两张图像计算得到直方图H1与H2，归一化到相同的尺度空间，然后可以通过计算H1与H2的之间的距离得到两个直方图的相似程度进而比较图像本身的相似程度。Opencv提供的比较方法有四种：

1. Correlation 相关性比较   ( CV_COMP_CORREL 0)
2. Chi-Square 卡方比较       ( CV_COMP_CHISQR 1) 
3. Intersection 十字交叉性   ( CV_COMP_INTERSECT 2)
4. Bhattacharyya distance 巴氏距离 ( CV_COMP_BHATTACHARYYA 3)

 OpenCV使用compareHist函数进行相似性计算，该函数返回一个数值，相关性方法范围为0到1,1为最好匹配，卡方法和Bhattacharyya距离法是值为0最好，而交集法为值越大越好。函数原型：

CV_EXPORTS_W double compareHist( InputArray H1, InputArray H2, int method );

//! compares two histograms stored in sparse arrays
CV_EXPORTS double compareHist( const SparseMat& H1, const SparseMat& H2, int method );

（1）相关性比较（Correlation）（method=CV_COMP_CORREL）

        相关性比较公式如下：

             

 其中： 

    N等于直方图中bin的个数。 如果H1 = H2，即两个图的直方图一样，分子等于分母，值为1，所以在不严格的情况下，当值为1时，可以认为两个图是一样的。但是也有可能会出现两个图不一样，但是两个图的直方图是一样的情况。因为直方图计算的是像素点个数的分布情况，但是不会显示像素点的位置，所以有可能会出现两幅图片不一样，但是相同像素的个数完全一样，那他们的直方图也是一样的，不过这种情况，不常有。

       相关性比较公式来源于统计学中的相关系数，是研究变量之间线性相关程度的量，一般用字母 r 表示。
                                                       

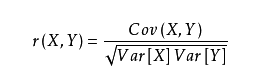
        其中，Cov(X,Y)为X与Y的协方差，Var[X]为X的方差，Var[Y]为Y的方差。

2）卡方，Chi-Square(method=CV_COMP_CHISQR)

                                                                  
   通过这个公式我们能够发现，卡方比较和相关性比较恰恰相反，相关性比较的值为0，相似度最低，越趋近于1，相似度越低；卡方比较则是，值为0时说明H1= H2，这个时候相似度最高。

    卡方比较来源于卡方检验，卡方检验就是统计样本的实际观测值与理论推断值之间的偏离程度，实际观测值与理论推断值之间的偏离程度就决定卡方值的大小，卡方值越大，越不符合；卡方值越小，偏差越小，越趋于符合，若两个值完全相等时，卡方值就为0，表明理论值完全符合。

    卡方检验的公式如下，其中fi是观测频率，npi是期望频率，X²是卡方值。

                                                         

3）Intersection（十字交叉性）(method-CV_COMP_INTERSECT)

                                                      
    这个就比较简单了，对比H1,H2并求出最小值，最后求和。

 4）Bhattacharyya距离，（method=CV_COMP_BHATTACHARYYA）

 定义：对于在X 数域上的两个离散概率分布p 和q，巴氏距离定义为： DB(p,q) = -ln(BC(p,q))

其中 BC(p,q) = Σsqrt(p(x)*q(x))，BC 被称作Bhattacharyya 系数（巴氏系数），0≤BC≤1 且0≤DB≤∞

     巴氏系数全称为巴塔恰里雅(Bhattacharyya coefficient) 系数,是向量相似度匹配中(如：用于衡量参考模版与候选模版的颜色概率分布的相似度或者说相关性测量)最常用的小算法。

              
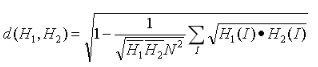
      在直方图相似度计算时，巴氏距离获得的效果最好，但计算是最为复杂的。巴氏距离的计算结果，其值完全匹配为1，完全不匹配则为0。上式中的分数是一个归一化系数。

图像相似性度量-------EMD

      EMD算法是用来比较两幅图像相似性的方法。在颜色直方图中，由于光线等的变化会引起图像颜色值的漂移，它们会引起颜色值位置的变化，从而导致直方图匹配失效。对于两个形状相同，但只是相对平移的两个直方图，距离度量会给出一个很大的值，我们需要一个对这种平移不敏感的距离度量方法。EMD的思想是求得从一幅图像转化为另一幅图像的代价，用直方图来表示就是求得一个直方图转化为另一个直方图的代价，代价越小，越相似。所以EMD可以理解为：直方图A转化为直方图B时，需要把A中的每一个bin进行分割给B中的每一个bin，在乘上bin之间的代价。

     先介绍一下signature的概念。大家都知道，一个图像的直方图就是把图像像素值量化为一系列bin，统计落在相应bin的像素个数，就形成了直方图。

signature的定义为：，    对于一个一维直方图，m为直方图的bin索引，w为该bin上的数量。它代表了一系列特征类别。每个s代表一类特征，m为其类中心，w为属于该类中心的数量。

    为什么要用signature呢？作者的说法是经常性的直方图的内容会聚集在某些bin上，而传统的完整表达的直方图显然太过于浪费空间。而用signature可以很方便的表达比较稀疏的直方图内容。（一个灰度图形成的一维直方图可能不会稀疏，但是想象一个三维直方图，它可能就会比较稀疏了）

EMD本身是一个线性规划问题。定义如下两个signature P和Q，分别有m和n个类。
                                            

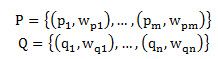
    另外定义一个类别的距离矩阵，每一项为pi和qj的距离（在均匀的直方图中，距离就可以简化为bin的索引的差值的绝对值）。可以发现它是mxn的矩阵::

那么问题就是我们希望找到一个矩阵[]，每一项代表从pi到qj的流动数量，从而最小化整体的代价函数：

                                                 
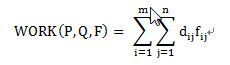
     这里就可以把EMD的本质说出来了，说白了，就是把P中的m个坑的土，用最小的代价搬到Q中的n个坑中，pi到qj的两个坑的距离由dij来表示。是从pi搬到qj的土的量；是pi位置到qj位置的代价（距离）。要最小化WORK工作量。EMD是把这个工作量归一化以后的表达，即除以对的求和。

    假如：A和B都有两个bin，且A到B的距离代价分别为d11=0.4和d12=0.7,d21=0.2,d22=0.6；A的bin1为0.5，且分成0.1和0.4给B的bin1和bin2，同样，A的bin2分成0.3和0.2给B的bin1和bin2,则EMD=0.1*0.4+0.7*0.4+0.2*0.3+0.6*0.2 

EMD( InputArray signature1, InputArray signature2,
                      int distType, InputArray cost=noArray(),
                      float* lowerBound=0, OutputArray flow=noArray() );

• signature1 大小为 size1×(dims+1) 的浮点数矩阵，每一行依次存储点的权重和点的坐标。矩阵允许只有一列（即仅有权重），如果使用用户自定义的代价矩阵。 
• signature2 与 signature1 的格式一样size2×(dims+1)，尽管行数可以不同(列数要相同)。当一个额外的虚拟点加入 signature1 或 signature2 中的时候，权重也可不同。
• distance_type 使用的准则， CV_DIST_L1, CV_DIST_L2, 和 CV_DIST_C 分别为标准的准则。  
• cost自定义大小为 size1×size2 的代价矩阵。
• flow 产生的大小为 size1×size2 流矩阵（flow matrix）: flowij 是从 signature1 的第 i 个点到 signature2 的第 j 个点的流(flow)。
• lowerbound 可选的输入/输出参数：两个签名之间的距离下边界，是两个质心之间的距离。如果使用自定义代价矩阵，点集的所有权重不等，或者有签名只包含权重（即该签名矩阵只有单独一列），则下边界也许不会计算。用户必须初始化 *lower_bound. 如果质心之间的距离大于获等于 *lower_bound (这意味着签名之间足够远）， 函数则不计算 EMD. 任何情况下，函数返回时 *lower_bound 都被设置为计算出来的质心距离。因此如果用户想同时计算质心距离和T EMD, *lower_bound 应该被设置为 0.

过程：

1. 把图像从RGB色彩空间转换到HSV色彩空间(因为直方图都是基于亮度和灰度级别,二HSV色彩空间对色彩亮度表示比较好的方式,转换成HSV空间以后然后只取HS通道)
2. 计算图像的直方图,然后归一化到[0~1]之间calcHist和normalize;
3. 使用上述四种比较方法之一进行比较compareHist.
    

实例展示：

a.加载图像

b.将图像从BGR空间转化为HSV空间

c.计算直方图并归一化处理

d.直方图比较

e.展示图像

#include
#include

using namespace std;
using namespace cv;

int main() {
//直方图相似度比较
	vector src;//迭代器push_back
	Mat temp = imread("0.jpg", 1);
	int m=temp.rows / 2;
	int n = temp.cols;
	//将一幅图分割为上下两部分
	Mat image_cut =Mat(temp, Rect(0, 0, n, m)).clone();//Rect(x,y,w,h)
	Mat image_cut2 = Mat(temp, Rect(0, m, n, m)).clone();
	src.push_back(image_cut); src.push_back(image_cut2);
	temp = imread("1.jpg", 1);
	src.push_back(temp);
	temp = imread("2.jpg", 1);
	src.push_back(temp);

	vector hsv(4), hist(4),hist_img(4);
	int scale=10,histSize[] = { 8,8 }, ch[] = { 0,1 };//30rows,32cols
	float h_ranges[] = { 0,180 };
	float s_ranges[] = { 0,255 };
	const float* ranges[] = { h_ranges,s_ranges };
	for (int i = 0; i < 4 ; i++) {
		cvtColor(src[i], hsv[i], COLOR_RGB2HSV);
		calcHist(&hsv[i], 1, ch, noArray(), hist[i], 2, histSize, ranges, true);
		normalize(hist[i], hist[i], 0, 255, NORM_MINMAX);
		hist_img[i]=Mat::zeros(histSize[0] * scale, histSize[1] * scale, CV_8UC3);
		for (int h = 0; h < histSize[0]; h++) {
			for (int s = 0; s < histSize[1]; s++) {
				float hval = hist[i].at(h, s);
				rectangle(hist_img[i], Rect(h * scale, s * scale, 10, 10), Scalar::all(hval), -1);
			}
		}
	}
	
	//display
	imshow("0", src[0]); imshow("1", src[1]); imshow("2", src[2]); imshow("3", src[3]);
	imshow("hist0", hist_img[0]); imshow("hist1", hist_img[1]); imshow("hist2", hist_img[2]); imshow("hist3", hist_img[3]);
	for (int i = 0; i < 4; i++)
	{
		cout << "hist[0] vs hist[" << i <<"]"<< endl;
		for (int j = 0; j < 4; j++) {
			cout << "method[" << j <<"]"<< compareHist(hist[0], hist[i], j)< sig(4);
	for (int i = 0; i < 4; i++) {
		vector sigv;
		normalize(hist[i], hist[i], 1, 0, NORM_L1);
		for (int h = 0; h < histSize[0]; h++) 
			for (int s = 0; s < histSize[1]; s++) {
				float hval = hist[i].at(h, s);
				if (hval != 0)
					sigv.push_back(Vec3f(hval, (float)h, (float)s));
			}
		sig[i] = Mat(sigv).clone().reshape(1);
		if (i > 0)
			cout << EMD(sig[0], sig[i], CV_DIST_L2) << endl;
	}
waitKey();
}

 结果：

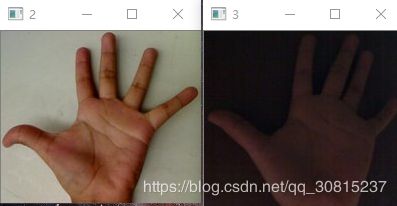
原图像src存放4张图片，0，1是一张亮的手掌图片的上下两部分，2，3亮度变暗，将4张图片转换HSV空间，计算直方图。

   

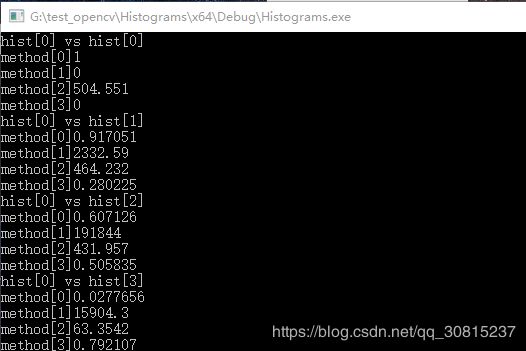
下面是图0与4张图片的直方图相似度的比较：

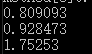
EMD结果：

from :https://blog.csdn.net/wangdonggg/article/details/32329879