编码的奥秘：存储器组织

转自：《编码的奥秘》  第十六章

 

 

          每天早上，当我们从睡梦中醒来时，记忆会填充大脑的空白。我们会记起我们在哪里，做过什么，计划做什么。我们可能一下子就能想起来，也可能几分钟都想不起来，不过，总的来说，我们通常能够重新组织自己的生活，保持高度的连续性，开始新的一天。
          当然，人类的记忆是无序的。当回忆高中的几何课时，你可能会想到是谁坐在你前面；或者那一天当老师要解释什么是 QED(quod erat demonstrandum，证完 /证毕 )的时候，刚好进行消防演习。

          人类的记忆也非安全无比。其实，书写的发明就是为了弥补人类记忆的不足。前一天晚上你可能因为突然冒出的一个关于剧本的好主意而在凌晨三点醒来，抓起床边特地准备的笔和纸记下来以便不会忘掉，第二天早上你就可以看到这个好主意并开始着手写剧本。当然你也可以不用这样。

          先写后读，先保存后取回，先存储后访问，存储器的作用就是在这两类事件间保证信息的完好无损。无论什么时候存储信息，都要用到不同类型的存储器。纸是保存文本信息的最佳媒体，磁带则能很好地保存音乐和电影。

        电报继电器—当集成为逻辑门然后再集成为触发器—也一样可以保存信息。正如我们所知道的，一个触发器可保存 1 位信息。保存 1 位信息当然并不代表保存全部信息，但这是一个开端。一旦我们知道了如何存储 1 位信息，就可以容易地存储 2位、 3位或更多位信息。

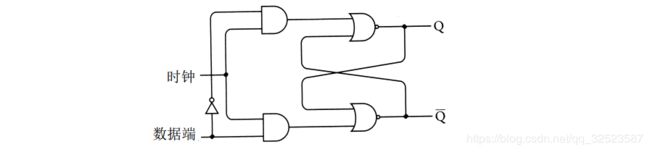
         第1 4章曾讲过电平触发的 D型触发器，它由一个反向器、两个与门和两个或非门构成：

         当时钟输入为1时，Q端输出与数据端输入是相同的。但当时钟输入变为0时，Q端输出将维持原来的数据端输入，再改变数据端输入不会影响Q端输出，直到时钟输入再次变为1为止。触发器的逻辑表格如下：
 

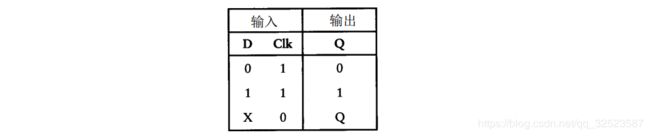
         在第 1 4章中，这种触发器的功能体现在两个不同的电路中。而在本章，它仅以一种方式来使用 —即用于保存 1 位信息。正因为如此，给输入端和输出端重新命名，以便与该目的更为一致。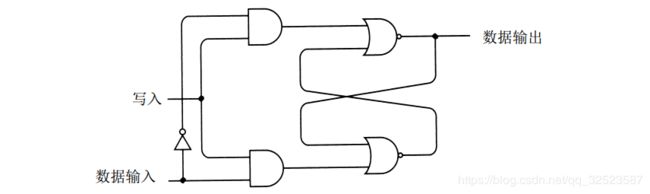
          这是同一个触发器，但现在 Q输出端命名为数据输出 （ Data Out），时钟输入端（在第 1 4章是作为保持位）命名为 写入 （ Wr i t e）。就像可以在纸上记录信息一样，写入信号使得数据输入（ Data In）信号写入或存储到电路中。通常，若写入信号 ( W )为0，则数据输入 ( D I )信号对输出无影响。而当我们想在触发器中存储数据输入信号时，写入信号应先置 1 后置0。就像在第1 4章提到的，这种类型的电路也叫 锁存器，因为它锁定数据。下面画出了一个 1 位锁存器，但没有画出其所包含的单个部件：

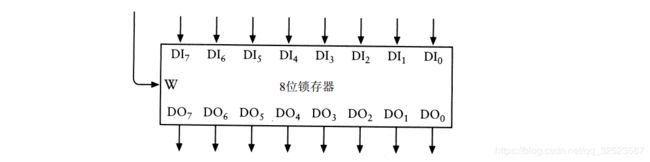
          把多个1 位锁存器连成多位锁存器是相当容易的，只需连接好写入信号：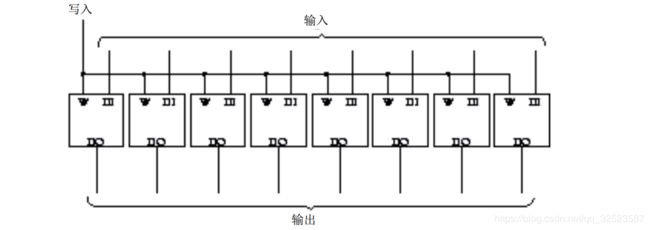
         该8位锁存器具有 8个输入端和 8个输出端。另外，这个锁存器有一个写入输入端，通常为0。要在这个锁存器中存储一个 8位二进制数，应将写入信号先置 1 后置0。也可以把这个锁存器画成一个整体，就像这样：

 

为了与 1 位锁存器一致，也可以画成这样：

          另外一种集成 8个1 位锁存器的方法不像上述这么直接。假设只想用一个数据输入信号端和一个数据输出信号端，且又希望它具备在一天或一分钟内存储 8次数据输入信号的能力。同时，也希望能通过检测这个数据输出信号端就可以检查这 8个数据。

          换句话说，我们只想存储 8个单独的 1 位数，而不想在 8位锁存器中存储 1 个8位数。
          为什么会有这种想法呢？可能是因为我们仅有一个灯泡的缘故吧！

           我们知道这需要 8个1 位锁存器。先不要考虑这些数据是怎样存储在这些锁存器中的，先让我们把注意力放在如何用一个灯泡来检查 8个锁存器的数据输出信号上。当然，我们通常用手工把灯泡从一个锁存器移到另一个锁存器来测试各个锁存器的输出，不过，我们更倾向于用更自动化的方法来实现。实际上，我们打算用开关来选择想要检查的锁存器。

           那么，需要多少个开关呢？若是 8个锁存器，则需要 3 个开关。 3个开关可表示 8个不同的值： 0 0 0、 0 0 1 、 0 1 0、 0 11 、 1 0 0、 1 0 1 、 11 0和111。

            目前已有8个1位锁存器、 3个开关、 1个灯泡，此外还有“其他东西”用在开关和灯泡之间：

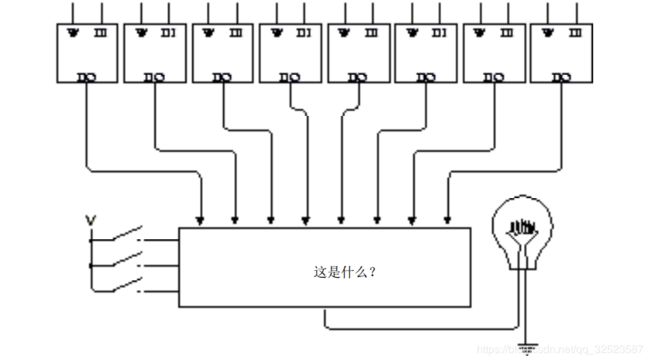
           这个“其他东西”就是标识为“这是什么？”的神秘盒子，它上面有 8个输入端，左侧有3 个输入端。通过闭合和断开这三个开关，就可以从 8个输入中选择一个，使其经过底部至输出端输出，该输出使灯泡发光。

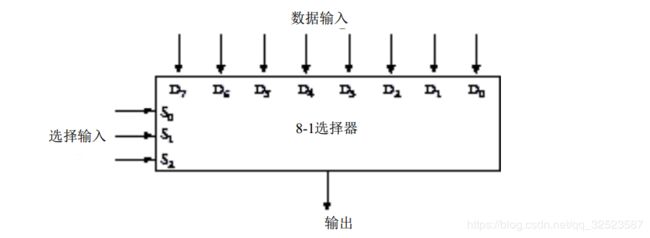
          “这是什么？”到底是什么呢？我们以前曾见过类似的东西，尽管没有这么多的输入端。它类似于第 1 4章中第一个改进的加法机里用到的电路。那时我们需要某种东西用于是选择一行开关还是选择一个锁存器的输出作为加法器的输入，我们把这种东西叫 2 - 1 选择器，这里需要8 - 1 选择器：

 

         8 - 1 选择器具有 8个数据输入端（显示在上部）和 3个选择输入端 (Select Input) （显示在左侧） ，选择输入端用于选择哪个输入数据在输出端输出。例如，若选择输入端为 0 0 0，则输出D0的值；若选择端为 111，则输出 D7的值；若选择端为 1 0 1 ,则输出 D5的值。其逻辑表如下：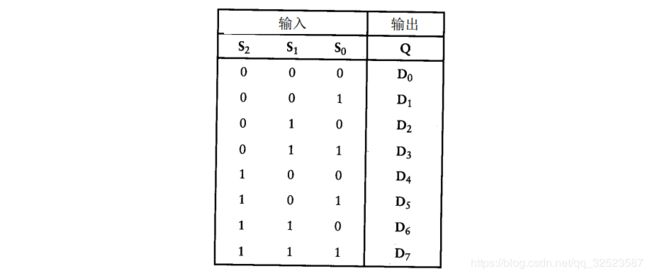

          8 - 1选择器由三个反向器、八个 4输入与门和一个 8输入或门构成，如下所示：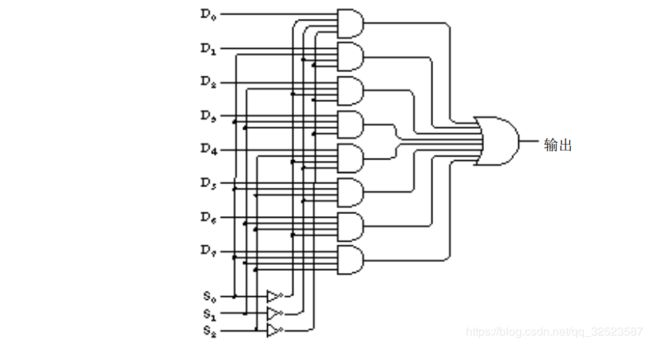
          这是一个相当复杂的电路，但只需一个例子就可以使你明白它是如何工作的。假设S2= 1 , S1= 0 , S0= 1 ，从上面数第六个与门的输入包括 S0、－S1、 S2,它们全为 1 。没有其他与门有同样的三个输入信号，因此，其他与门输出全部为 0。若D5＝0，则第六个与门输出为 0；若 D5＝1 ，则其输出为 1 。对最右边的或门来说也是如此。因此，若选择端为 1 0 1 ，则输出为 D5。

           概括一下我们想干什么。我们想连接 8个1 位锁存器，它们能够通过一个数据输入信号端分别写入，也能通过一个数据输出信号端分别检查。已经证明可以用一个 8 - 1 选择器从 8个锁存器中选择一个数据输出信号，如下图所示：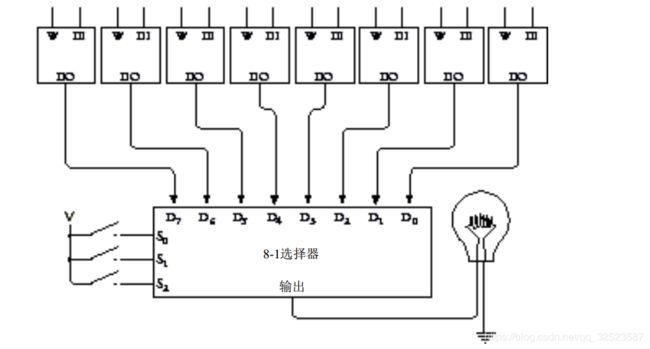

            到现在已完成了任务的一半。我们已经实现了输出端的要求，现在再来看一下输入端。

             输入端包括数据输入信号及写入信号。在锁存器的输入端，可以把所有数据输入信号连接在一起。但不能把 8个写入信号也都连在一起，因为我们还想分别向每个锁存器中写入数据。此外，还要有一个单独的写入信号，它必须能连到其中任一个（并且只能是一个）锁存器上：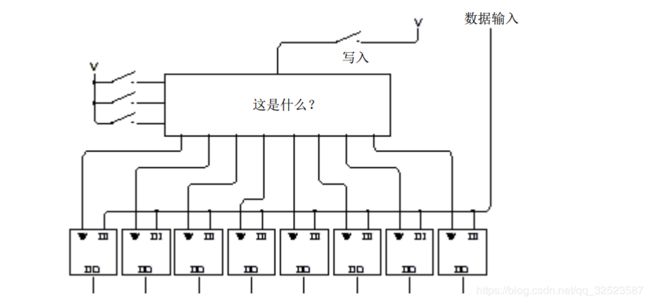

             为了完成这项工作，需要另外一个电路，这个电路看起来与 8 - 1 选择器有点相似，但实际上却正好相反。这就是 3 - 8译码器。前面我们曾见过简单的数据译码器—第11 章曾通过连接开关来选择理想的猫的颜色。

             3 - 8译码器有 8个输出端。任何情况下，锁存器除了一个输出端外，其余的均为 0。这个例外是由 S0、 S1、 S 2输入信号所选择的输出端。该输出端输出的也是数据输入端的输入：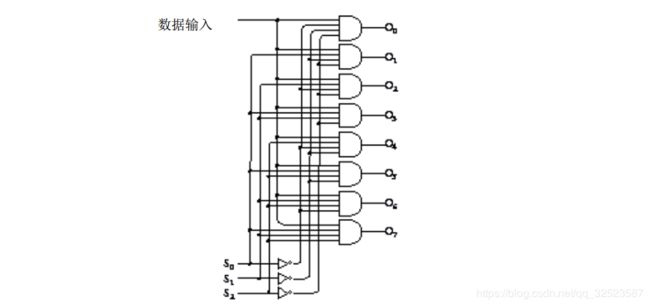

          再说一遍，从上面数第六个与门的输入包括 S0、-S1、 S 2，没有另外的与门有同样的三个输入。若选择输入端为 1 0 1 ，则其他与门输出都为 0。若数据输入为 0，则第六个与门输出为 0；若数据输入为 1 ,则其输出为 1 。其逻辑表格如下：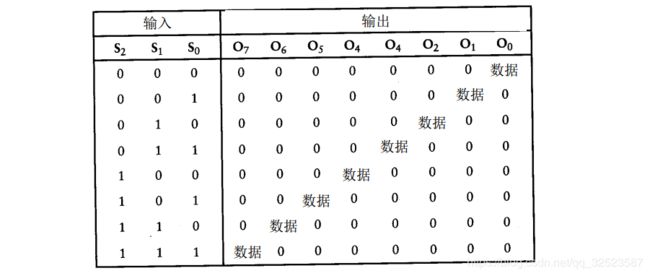
        下面是具有 8个锁存器的完整电路：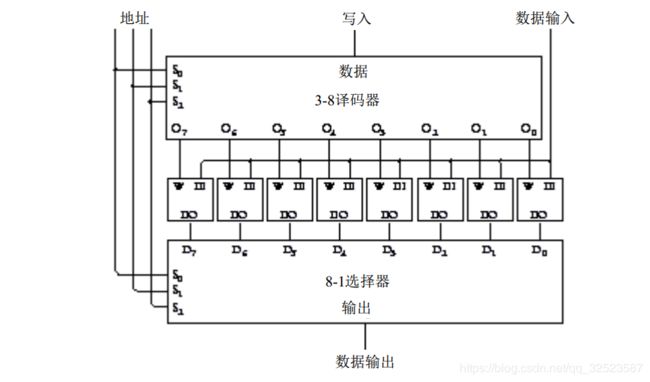

          注意，译码器和选择器的三个选择信号相同，现在这三个信号都记作 地址 （ A d d r e s s）。就像信箱号一样， 3 位地址决定了选择 8个锁存器中的哪一个。在输入端，地址输入决定写入信号触发哪一个锁存器来存储输入的数据。在输出端（图的下部） ，地址输入控制 8 - 1 选择器选择8个锁存器中的一个进行输出。

          这种锁存器的配置有时也称为读／写存储器，但通常叫作随机访问存储器或 R A M。 R A M可存储8个单独的 1 位数据，如下图所示：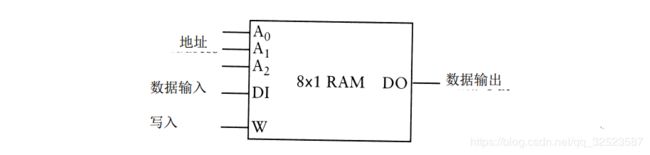

           称它为存储器是因为它能保存信息，称为读／写存储器是因为可以在每个锁存器中保存新的数据（也就是写数据） ，同时还可以查看每个锁存器中所保存的数据（也就是读数据） 。称它为随机访问存储器是因为通过简单地改变地址输入就可以从 8个锁存器中的任意一个读出或写入数据。相比之下，其他类型的存储器必须顺序读出—也就是，在可以读出存储在地址1 0 1 的数据之前，必须读出存储在地址 1 0 0的数据。

            R A M配置通常称作 R A M阵列 ，上述这种特定配置的 R A M阵列以简写形式 8× 1 的方式组织起来。阵列中可以存放8个数，每个仅占 1 位， R A M阵列中能存储的位数等于这两个值的乘积。

            R A M阵列可通过各种方法来组合。例如，可以把两个 8× 1 RAM 阵列连接起来，使它们按照相同的方法来寻址：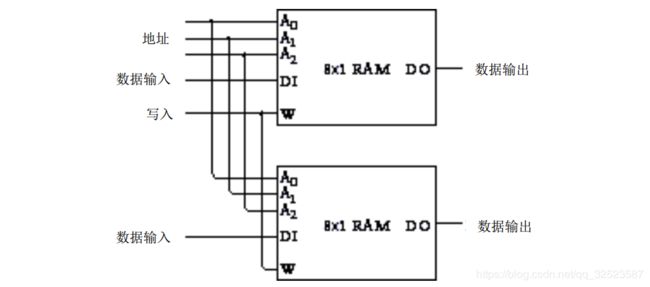
        这两个 8× 1 RAM阵列的地址和写入输入端连接在一起，所以其结果为一个 8× 2 RAM阵列：

          这个R A M阵列可存储 8个数，但每个数占 2位。

          两个8× 1 RAM阵列也可以按照与单个锁存器连接相同的方式—通过一个 2 - 1选择器和一个1 - 2译码器—来组合，如下图所示：

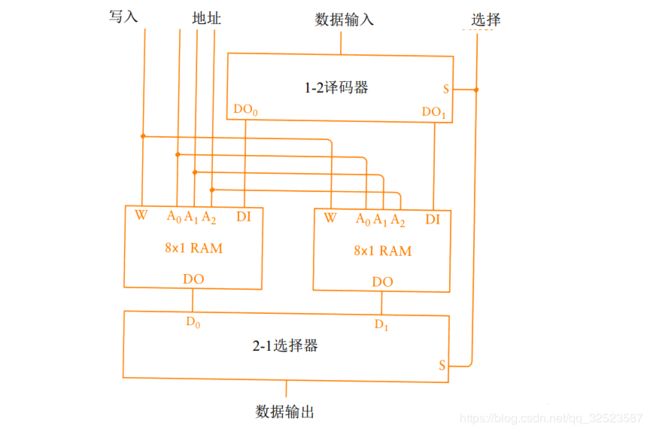
          连接到译码器和选择器的选择（ S e l e c t）输入实质上选择两个 8× 1 RAM阵列中的一个，在这里它也就是第 4根地址线。所以，该图实际上是一个 1 6× 1 RAM 阵列：

         此R A M阵列可存储 1 6个数，每个数占 1 位。

          R A M阵列的存储容量与地址输入端数目有直接关系。无地址输入端时（即 1 位锁存器和 8位锁存器这种情况），只能存1 个数；有一个地址输入端时，可存 2个数；有两个地址输入端时，可存 4个数；有三个地址输入端时，可存 8个数；有四个地址输入端时，可存 1 6个数。其关系可归纳成如下等式：

            上面已讲了如何构造小的 RAM 阵列，那么再规划大的 RAM 阵列应该并不困难。例如：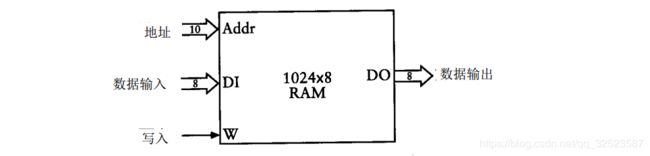
           这个R A M阵列可存储 8 1 9 2位信息，按 1 0 2 4个数、每个 8位来组织。因为，所以它有1 0条地址线。此外，它有 8个数据输入端和 8个数据输出端。

          换句话说，这个 RAM 阵列可存储 1 0 2 4个字节。就像一个邮局有 1 0 2 4个邮箱，每个信箱中有一个不同的 1 字节数。

 

          1 0 2 4个字节即 1K 字节（ k i l o b y t e）， 1 K字节在此会引起许多混淆。公制里前缀 k（来自于希腊文 k h i l i o i ,意思为 1 千）经常用到，如 1 k g = 1 0 0 0 g , 1 k m = 1 0 0 0 m。但这里所说的 1 K字节= 1 0 2 4字节—而非1 0 0 0字节。

           原因在于公制是基于 1 0的幂，而二进制是基于 2的幂，这两种进制永远不会有相同的值。1 0的整数次幂为 1 0、 1 0 0、 1 0 0 0、 1 0 0 0 0、 1 0 0 0 0 0等，而 2的整数次幂为 2、 4、 8、 1 6、 3 2、 6 4等，没有 1 0的整数次幂与 2的整数次幂相等的情况。

            但有时它们非常接近。的确， 1 0 0 0非常接近 1 0 2 4，可以用“约等于 (≈ )”符号进行数学化表示：

             这个关系式并非不可思议，它只不过表明 2的某次幂等于 1 0的某次幂而已。这种特例允许人们方便地把 1 0 2 4字节称作 1 K字节。

            K字节简写为 K或K B。所以，上面展示的 R A M阵列存储 1 0 2 4字节或1 K ( 1 K B )。

            不能把 1 K B的R A M阵列说成是存储 1 0 0 0字节，它大于 1 0 0 0，即 1 0 2 4，为了让人知道你在说什么，你可以把它说成“ 1 K”或“ 1 K字节”。

            1 K字节的存储器具有 8个数据输入端， 8个数据输出端和 1 0个地址输入端。由于是通过 1 0条地址线来访问字节，所以 R A M阵列可存储 2 1 0个字节。无论何时再加上一条地址线，其存储容量将翻倍。下面每一行都都表示存储容量的翻番：
             可以看出左侧的数字也是 2的整数次幂。

             按照同样的逻辑，我们能把 1 0 2 4 字节称作 1 K B ，当然也可以把 1 0 2 4 K B 称作 1 M 字节（ m e g a b y t e，希腊文 m e g a s意思为大） ， M字节缩写为 M B。以下仍是存储容量翻番的式子：

           希腊文 g i g a s意思为巨大，所以把 1 0 2 4 M B称作1 G字节( g i g a b y t e )，缩写为 G B。\

           同样， 1 T字节( t e r a b y t e，希腊文 t e r a s意思为庞然大物）等于 2 4 0字节（约 1 01 2）或1 099 511627776B,terabyte缩写为 T B。

           1KB约为1000B， 1MB约为1 000 000B,1GB约为1 000 000 000B,1TB约为1 000 000 000 000B。

           再大的数就很少用了，如 或1 125 899 906 842 624 字节，约等于。 或1 152 921 504 606 846 976字节，约等于 。

            下面提供一些基本常识。在此书编写的时候（ 1 9 9 9年） ，家用电脑一般都配有 3 2 M B 或6 4 M B或1 2 8 M B的随机访问存储器（为不至于混淆，这里不谈任何关于硬盘驱动器的事情，而只谈论R A M），即 33 554 432B或67 108 864B或134 217 728B。

             当然，人们总拣方便的讲。有 65 536 字节内存的人会说“我有 6 4 K”；有 33 554 432字节的人会说“我有 3 2 M”。虽说不多，但有 1 073 741 824字节的人也会说“我有 1 G”。

              有时人们可能会提到 K位或M位（注意是位而不是字节） ，不过这很少见。人们谈到存储器时，几乎总是指字节数而非位数。 （当然，把字节转换成位，乘 8即可。 ）在线路传送数据时，通常会有这样的短语每秒千位(k b p s )或每秒兆位(m b p s )出现。例如， 5 6 K的调制解调器指的是5 6 K b p s ,而非每秒千字节。

              至此我们已经明白如何构造所需的 R A M阵列，但不要离题太远。现在让我们看一下已经集成了 65 536字节的存储器：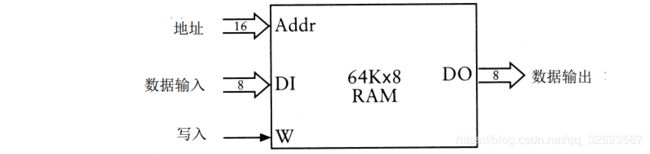
          为什么是6 4 K B而非3 2 K B或1 2 8 K B？因为65 536是一个整数，刚好为，也即该R A M阵列有 1 6位地址。换句话说，该地址正好是 2个字节。用十六进制来表示其地址范围是 0 0 0 0 h～FFFFh。、

            6 4 K B的内存在 1 9 8 0年的 P C机上是比较普遍的配置，尽管它不是用电报继电器制成的。但是，你真的能用继电器来实现吗？肯定不能。因为按照我们的设计方案需要为每位存储器提供9个继电器，那么 6 4 K× 8的R A M阵列需要将近 5 0 0万个继电器。

            利用控制面板来操作所有的存储器—写入数据到存储器或验证写入的数据—将更加先进。这种控制面板用 1 6个开关来表示地址， 8个开关来表示需要输入存储器的 8位数据， 8个灯泡来显示 8位数据，再用一个开关来表示写入信号，如下图所示：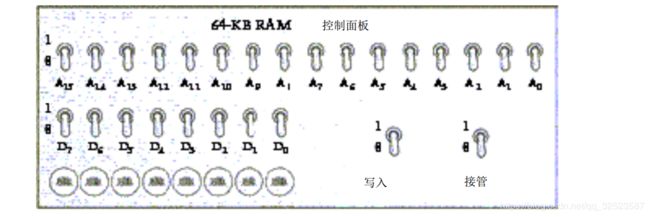

            所有的开关均显示在 0位置。另外，还有一个标识为接管 ( t a k e o v e r )的开关，使用这个开关的目的是使其他电路可以使用与控制面板相连的同一个存储器。 当接管开关置 0时（如图所示），控制面板上的其余开关将不起任何作用；而当此开关置 1 时，控制面板将对存储器进行专门控制。

             这些都可以用若干 2 - 1 选择器来实现。实际上，需要 2 5个—1 6个接地址信号、 8个接数据输入开关、另外 1 个接写入开关。其电路如下：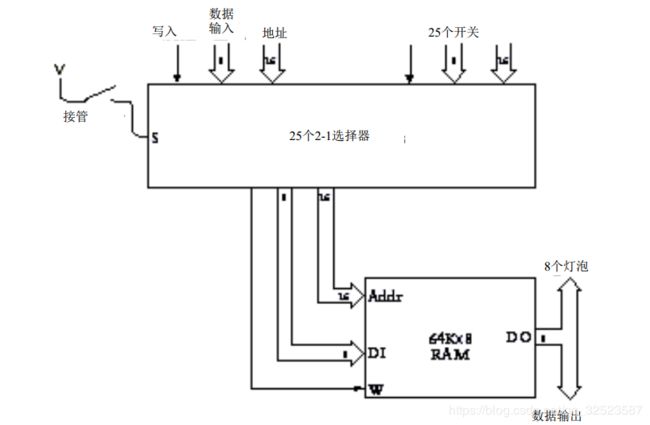

        当接管开关断开时（如上图） ， 6 4 K× 8 RAM阵列的地址、数据输入和写入信号来自于外部信号，显示在 2 - 1 选择器的左上角；当接管开关闭合时， R A M阵列的地址、数据输入和写入信号来自于控制面板开关传来的信号。无论哪种情况， R A M阵列的数据输出信号传到 8个灯泡上或其他可能的地方。

          下图是带有控制面板的 6 4 K× 8 RAM 阵列：

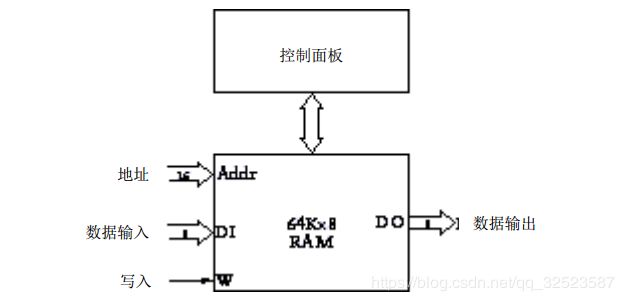
         当接管开关闭合时，可用 1 6个地址开关来选择 65 536 个地址中的任何一个，而灯泡将显示当前地址中所存的 8位数据。可用 8个数据开关来定义一个新数，并通过写入开关把它写入存储器中。

         通过6 4 K× 8 RAM阵列和控制面板可以与需要处理的 65 536 个8位数据中的任何一个保持联系。但我们也留了一些机会让别的东西—也许是其他一些电路—使用存在存储器中的数据，或者把数据写入存储器。

         还有一个必须注意的有关存储器的问题，它非常重要。在第 11 章介绍逻辑门的概念时，并未画出构成逻辑门的单个继电器的构造。特别地，没有标出每个继电器连接的电源。任何时候当继电器触发时，电流流过电磁线圈并在适当的位置吸下金属簧片。

         如果一个装满 65 536字节的 6 4 K× 8 RAM阵列被关掉电源，将会发生什么情况呢？所有的电磁铁将失去磁性，所有继电器的触点将回到未触发状态， R A M中的内容也将永远丢失。

 

         这就是随机访问存储器也称为易失性存储器的原因，它需要恒定的电源来保持其中的内容。