带花树算法 UOJ#79. 一般图最大匹配
带花树算法
能解决的问题:一般图最大匹配http://uoj.ac/problem/79
匈牙利算法可以解决二分图匹配的问题,但是因为二分图有一个特殊的性质,那就是不会出现一个有奇数点的环。然而对于每一个有偶数点的环,在环里面无论怎么匹配都是可以的,然而假如有奇数的环就不一样了。
不想写废话了。。
————————————正文——————————
时间复杂度大概是O(n^2)吧
首先,思路肯定是找增广路,也是让每一个没匹配的点去尝试进行匹配,看是否可以有新的匹配。
首先,在没出现奇环之前,我们把他当做一个普通的二分图来看,是没毛病的。
于是有了id这一个数组,id有三种不同的状态
-1:没访问过 0:S点 1:T点
首先我们假设一开始要增广的点是一个S点
由于写的是广搜,所以我们需要一个数组,pre,表示,假设在这次匹配中,第i个点的配偶根别人跑了,他该和谁配对。
然后对于找到方案的这一段代码就很简单了。。
那么接下来的问题是如何来进行寻找增广路的操作了
假设现在我们在队列中待处理的点为x
首先,假如我们遍历到一个以前没有访问过的点y,那么我们就让他的配偶继续进行增广。
Q:为什么是让他的配偶去呢?
A:因为我们现在是要假设x要与y相连啊,拿肯定是看看y的配偶是否可以换人啦,这一步感觉和普通的匈牙利是没什么太大的不同的
然后我们可以发现一个问题啊,那就是我们每一个待扩展的点x都是一个S点,嗯,都是S点。这就说明每一个点都是由S点扩展出来的。
那么除了上面的情况外,剩下的就是环了
假设我们出现的是一个偶环,那么就直接无视——至于为什么,大概想一下就可以了
假如我们发现的是一个奇环,那就有大大的不一样了,因为假如我们这个环中有任意一个点可以在外面找到增广路的话,这个环就变成了一个偶数环,问题就解决了。
比如说上面这个图,X就是我们要增广的点,假如出现了这样一个环,那么只要1,2,3,4随便一个点可以找到增广路,那么X就可以有配偶啦^_^
然后下文我们假设这个环的突然出现时因为出现了2————3这一条边
铺垫:我们在处理完一个奇环后,我们是可以把他试做一个点的(因为这个环中只要有一个点成功就行),所以这里写了一个并查集,来使点变成一个环,我的并查集下文用的是f,当然,这个大点是一个S点。
那么我们怎样知道他是不是一个奇环呢?
也很简单,只要我们访问到的点也是S点就是了。这个自己想一下应该也可以想出来
那么剩下的操作就是如何让他们去遍历了。
首先我们要知道这个环长什么样吧,比如说在上图中,2,3肯定是由之前的同一个点增广时所牵扯出来的,也就是有一个点使得他们间接连通现在才回出现环,上图就是x,所以我们要先知道他是从哪里来的。于是我们需要一个lca,当然这个lca也写得比较巧妙~~
然后就是处理环了,分两段进行,
一段就是处理2到x这一条路,另一段就是处理3到x这一条路,两个的操作是一样的,所以只需要写一个就可以了。
其中一个操作肯定是让图中所有的点去增广,因为一开始的S点肯定都已经入队增广了,所以我们要新加入的点就只有之前的T点了。
其次就是维护pre了,这个过程也比较简单,就是先让出现新边的两条pre互连,然后让上面的每一个T点与扩展他的S点相连。然后假如我们在其中任意有一个点找到增广路了,根据pre,你就可以得出一条没有冲突的匹配关系。这个我觉得自己脑补一下就好了。
还是举个栗子吧。。
还是上面的图,假如你现在T点4找到了增广路,那么3就会去找2,2的原配偶1就会去找x。
假如是S点3找到了增广路,那么4就会找到x,1,2关系不用变,这个和没环没啥区别。
完结撒花~~
全代码大部分都是照着别人的写的。。
#include
#include
#define swap(x,y) {int tt=x;x=y;y=tt;}
const int N=505*2;
const int M=124750*2;
int f[N];
struct qq
{
int x,y;
int last;
}s[M];
int num,last[N];
int n,m;
void init (int x,int y)
{
num++;
s[num].x=x;s[num].y=y;
s[num].last=last[x];
last[x]=num;
}
int match[N];
int id[N];//这个点是什么点
//-1:没访问过 0:S点 1:T点
int q[N];//要扩展的队列————也就是我们要尝试帮谁换配偶
int pre[N];//在这次过程中,x的新配偶是谁
int Tim,vis[N];//对于lca的标记以及时间轴
int find (int x)
{
if (f[x]==x) return f[x];
f[x]=find(f[x]);
return f[x];
}
int lca (int x,int y)//寻找lca
{
Tim++;
while (vis[x]!=Tim)
{
if (x!=0)
{
x=find(x);//先找到花根
if (vis[x]==Tim) return x;
vis[x]=Tim;
if (match[x]!=0) x=find(pre[match[x]]);
//因为在之前我们知道,每一个S点的配偶(也就是T点)的pre 都是指向他的父亲的,于是就直接这么跳就可以了
//还有要注意的是,一定要先去到花根,因为他们现在已经是一个点了,只有花根的pre才指向他们真正的父亲
else x=0;
}
swap(x,y);
}
return x;
}
int st,ed;
void change (int x,int y,int k)//环 出现的是x---y的连边 已知根是k
{
while (find(x)!=k)
{
pre[x]=y;
int z=match[x];
id[z]=0;q[ed++]=z;if (ed>=N-1) ed=1;
if (find(z)==z) f[z]=k;
if (find(x)==x) f[x]=k;
y=z;x=pre[y];
}
}
void check (int X)//尽量帮助x寻找增广路
{
for (int u=1;u<=n;u++) {f[u]=u;id[u]=-1;}
st=1;ed=2;
q[st]=X;id[X]=0;
while (st!=ed)
{
int x=q[st];
for (int u=last[x];u!=-1;u=s[u].last)
{
int y=s[u].y;
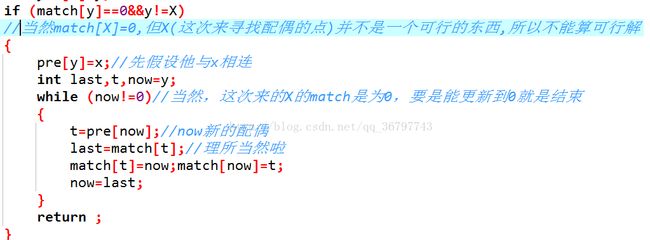
if (match[y]==0&&y!=X)
//当然match[X]=0,但X(这次来寻找配偶的点)并不是一个可行的东西,所以不能算可行解
{
pre[y]=x;//先假设他与x相连
int last,t,now=y;
while (now!=0)//当然,这次来的X的match是为0,要是能更新到0就是结束
{
t=pre[now];//now新的配偶
last=match[t];//理所当然啦
match[t]=now;match[now]=t;
now=last;
}
return ;
}
if (id[y]==-1)//找到一个没有访问过的点————进行扩展
{
id[y]=1;
pre[y]=x;//先假设他与x相连
id[match[y]]=0;q[ed++]=match[y];
if (ed>=N-1) ed=1;
}
else if (id[y]==0&&find(x)!=find(y))//出现一个以前未处理过的奇环
{
int g=lca(x,y);
change(x,y,g);change(y,x,g);
}
}
st++;
if (st>=N-1) st=1;
}
}
int main()
{
memset(vis,0,sizeof(vis));Tim=0;
memset(match,0,sizeof(match));
num=0;memset(last,-1,sizeof(last));
scanf("%d%d",&n,&m);
for (int u=1;u<=m;u++)
{
int x,y;
scanf("%d%d",&x,&y);
init(x,y);init(y,x);
}
for (int u=1;u<=n;u++)
if (match[u]==0)
check(u);
int ans=0;
for (int u=1;u<=n;u++)
if (match[u]!=0) ans++;
printf("%d\n",ans/2);
for (int u=1;u<=n;u++) printf("%d ",match[u]);
return 0;
} 肯定写错了很多东西。。。。。。