遗传算法在TSP问题上的应用matlab仿真实现

最近在做一个遗传算法应用的课程大作业，在网上找了一些TSP的算法，结合别人的算法进行更改和优化了下，得到了最终的仿真结果，感谢前人栽的树。

 

遗传算法在TSP问题上的应用

本文采用遗传算法来求解TSP问题，将中国的35个省会级城市作为研究对象，设置西安为起点，历经其余34座城市后，最后回到西安的一条最短路径。

一、设计过程

1、适应度函数设计：

TSP的目标是路径总长度为最短，在进行选择时更具适应度值越大则被遗传到下一代的概率越大，适应度值与路径总距离呈反比关系，因此路径总长度的倒数就可以为TSP的适应度函数：

  

2、序表达式编码

序表达式是TSP问题的最自然的表达，其中城市是按访问的顺序排列的。例如，对于9个城市的TSP:3-2-5-4-7-1-6-9-8-3可简单表示为向量[3254716983]，表示从城市3出发依次经过2,5,4,7,1,6,9,8然后返回城市3的一条路径。

3、联赛选择算子设计

联赛选择是基于个体适应度之间大小关系的选择方法,一般为两两比较,不需要满足f(x)>0,具体步骤为将群体中随机选N个个体进行适应度值大小比较,将大的个体遗传,将上述过程重复M次就可以得到M个个体。在本次设计中，随机从父代种群中选择4个路径个体，进行适应度值比较，将适应度最大的个体遗传到下一代，种群规模为200，则重复该选择步骤200次，得到新一代种群。

4、顺序交叉算子设计

顺序交叉(OX)：从父代A随机选择一个编码子串片段，放到子代A的对应位置，子代A空余的位置从父代B中按照B的顺序选取（与已有的编码不重复）。同理可得子代B。设置父代A=872|139|0546，父代B=983|567|1420。交叉过程:对于父代A,选择139进行遗传到下一代，其余部分从父代B中按照期序随机选取，从父代B中选择的元素不能和1、3、9散字相同，依次放到子代的对应位置，得到下一代A1，子代B1的求解过程同上，求解过程如下。

                                

5、两点对换变异算子设计(Mutation)

在本文中采用两点对换变异算子对种群进行变异操作，由于TSP问题的约束为路径中每个城市只能遍历一次，因此不能采用遗传算法常用的基于二进制编码的变异操作，不能由简单的变量进行翻转来实现变异。两点对换变异算子为在TSP问题中的个体编码是一系列城市的序列，随机在这个城市序列中抽取两个城市，然后交换他们的位置，这样就实现了个体的变异操作。

二、仿真结果如下：
 1、遗传算法的基本运算步骤
 （1）初始化：设置进化代数计数器t=0，设置最大进化代数T，随机生成M个个体作为初始群体P(0)。（2）个体评价：计算群体P(t)中各个个体的适应度。（3）选择运算：将选择算子作用于群体。选择的目的是把优化的个体直接遗传到下一代或通过配对交叉产生新的个体再遗传到下一代。选择操作是建立在群体中个体的适应度评估基础上的。（4）交叉运算：将交叉算子作用于群体。遗传算法中起核心作用的就是交叉算子。（5）变异运算：将变异算子作用于群体。即是对群体中的个体串的某些基因座上的基因值作变动。群体P(t)经过选择、交叉、变异运算之后得到下一代群体P(t+1)。（6）终止条件判断：若t=T,则以进化过程中所得到的具有最大适应度个体作为最优解输出，终止计算。

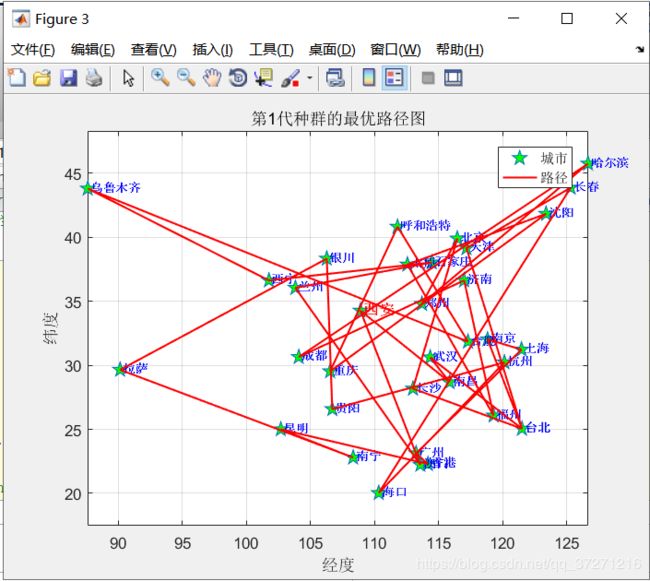
 2、初始种群路径图：

 

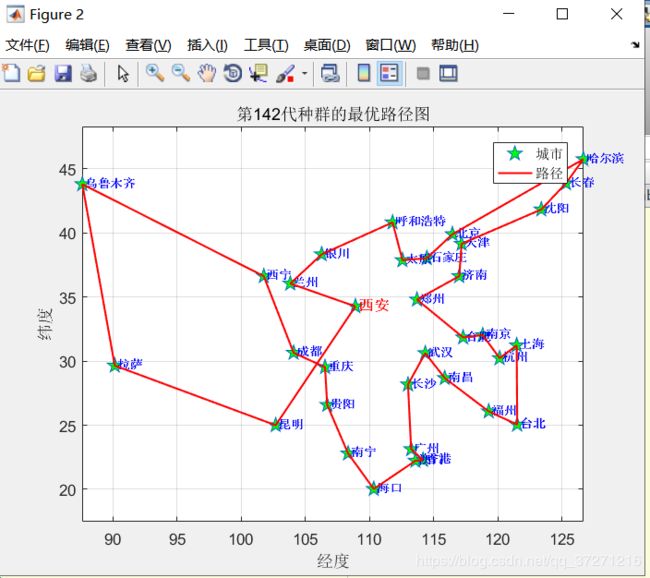
3、迭代找到最优解的路径图

4、收敛曲线图

 

 

 

 

 

二、具体matlab代码如下：

 

主函数main.c

clear;
clc;
tStart = tic; % 算法计时器
%************************初始化参数变量*******************************
    [Num,Txt,Raw]=xlsread('provincial_ capital_coordinate12.xlsx');  %经纬度数据
    cities = Num(:,5:6);
    cities=cities';
    [~,cityNum]=size(cities);
    
    
    maxGEN = 500;
    popSize = 300; % 遗传算法种群大小
    crossoverProbabilty = 0.95; %交叉概率
    mutationProbabilty = 0.33; %变异概率

    %********初始化种群***********
    % 计算上述生成的各个城市之间的距离断
    distances = calculateDistance(cities);
    % 生成种群，每个个体代表一个路径
    gbest = Inf;%行：Inf 无穷大
    parentPop = zeros(popSize, cityNum);
    % 随机打乱种群
    for i=1:popSize
     parentPop(i,2:cityNum-1) = randperm(cityNum-2); %randperm功能是随机打乱一个数字序列，将1-cityNum数字序列随机打乱
     for a=2:cityNum-1
         parentPop(i,a)=parentPop(i,a)+1;
     end
     parentPop(i,1)=1;
     parentPop(i,cityNum)=cityNum;
    end
    % 定义子代种群
    childPop = zeros(popSize,cityNum);
    
    %定义每代的最小路径
    minPathes = zeros(maxGEN,1);
    %****************************
  
%**********************************************************************

%*********************GA算法选择交叉变异执行过程************************
for  genNum=1:maxGEN
 
    % 计算适应度的值，即路径总距离
    [fitnessValue, sumDistance, minPath, maxPath] = fitness(distances, parentPop);
    tournamentSize=4; %设置大小
    for k=1:popSize
    %% 以下为联赛选择法
        % 随机选择父代
        tourPopDistances=zeros( tournamentSize,1);
        for i=1:tournamentSize
            randomRow = randi(popSize);%行：返回一个介于1到popSize的伪随机整数
            tourPopDistances(i,1) = sumDistance(randomRow,1);
        end
 
        % 选择最好的，即距离最小的
        parent1  = min(tourPopDistances);
        [parent1X,parent1Y] = find(sumDistance==parent1,1, 'first');%选出随机的4个中最短距离种群序号
        parent1Path = parentPop(parent1X(1,1),:);%%选出随机的4个中最短距离种群路径
 
 
        for i=1:tournamentSize
            randomRow = randi(popSize);
            tourPopDistances(i,1) = sumDistance(randomRow,1);
        end
        parent2  = min(tourPopDistances);
        [parent2X,parent2Y] = find(sumDistance==parent2,1, 'first');
        parent2Path = parentPop(parent2X(1,1),:);
    %% 以上为联赛选择法
  
    %% 顺序交叉（OX）
        individual = crossover(parent1Path, parent2Path, crossoverProbabilty);%个体交叉
    %%
  
    %% 对换变异（由于路径不能出现重复元素，因此变异不能为随意变化，本实验采用随机交换两元素位置来实现变异）
        individual = mutate(individual, mutationProbabilty);%个体变异
    %%
        childPop(k,:) = individual(1,:);%行：保存下一代种群的个体
        
        minPathes(genNum,1) = minPath; %行：保留此代中最短路径
    end
    % 更新父代
    parentPop = childPop;%行：种群此时更新为最新子代
    
    %% 画图

    % 画出当前状态下的最短路径
    if minPath < gbest
        gbest = minPath;
        paint(cities, parentPop, gbest, sumDistance,genNum);%行：画出最新的最短路径轨迹
    end
    fprintf('代数:%d   最短路径:%.2fKM \n', genNum,minPath);
  
%    fprintf('%s\n', Txt(Bestpath(1,0),2));
    %%
end

%% 迭代完成，进行最终结果显示
figure 
plot(minPathes, 'MarkerFaceColor', 'blue','LineWidth',1);
title({'最短路径收敛曲线图';['最短路径距离为', num2str(minPath)]});
set(gca,'ytick',0:10:450); 
ylabel('路径总长度');
xlabel('种群代数');
grid on
tEnd = toc(tStart);
fprintf('时间:%d 分  %f 秒.\n', floor(tEnd/60), rem(tEnd,60));

根据经纬度计算城市间距离函数：calculateDistance.m

function [ distances ] = calculateDistance( city )
%计算距离
 
    [~, col] = size(city);
    distances = zeros(col);
    for i=1:col
        for j=1:col
            distances(i,j)= distances(i,j)+ sqrt( (city(1,i)-city(1,j))^2 + (city(2,i)-city(2,j))^2  );           
        end
    end
end

交叉函数：crossover.m

function [childPath] = crossover(parent1Path, parent2Path, prob)
% 交叉
 
    random = rand();
    if prob >= random                     %行：随机生成一个01之前的数，和概率值比较，相当于一个轮盘赌的选择，来执行概率选择执行操作
        [l, length] = size(parent1Path);
        childPath = zeros(l,length);
        setSize = floor(length/2) -1;     %行：floor 朝负无穷大方向取整
        offset = randi(setSize);          %行：随机 产生1-setSize之间的整数
        parent1OXstart=offset;            %行：0X交叉，父代1遗传给子代的片段起点
        parent1OXend=setSize+offset-1;    %行：0X交叉，父代1遗传给子代的片段终点
        
        for i=parent1OXstart:parent1OXend
            childPath(1,i) = parent1Path(1,i);
        end
        
        childPath(1,1) = parent1Path(1,1);%行：将路径的起点和终点直接赋给子代，因为起点和终点不变
        childPath(1,length) = parent1Path(1,length);
        
        %行：parent2依顺序放入子代位坐标
        parent2Point=2;                
        for x=2:length-1
            if childPath(1,x)==0
                for y=parent2Point:length-1
                    if ~any(childPath == parent2Path(1,y))%行：如果子代路径相应元素不等于父代元素
                        childPath(1,x)=parent2Path(1,y);
                        parent2Point=y+1;
                        break;
                    end
                end
            end
        end
        
    else
        childPath = parent1Path;
    end
end

变异函数：mutate.m

function [ mutatedPath ] = mutate( path, prob )
%对指定的路径利用指定的概率进行更新
%行：由于路径不予许存在相同的数，所以变异不能随意变，只能用随机互换位置的方法
    random = rand();
    if random <= prob         
        [l,length] = size(path);
        index1 = randi([2,length-1]);
        index2 = randi([2,length-1]);
        %交换
        temp = path(l,index1);
        path(l,index1) = path(l,index2);
        path(l,index2)=temp;
    end
        mutatedPath = path; 

结果路径图片显示函数：paint.m

function [ bestPopPath ] = paint( cities, pop, minPath, totalDistances,gen)
    gNumber=gen;
    [~, length] = size(cities);
    xDots = cities(1,:);
    yDots = cities(2,:);
    %figure(1);
    %行：先画城市的固定坐标
    plot(xDots,yDots, 'p', 'MarkerSize', 10, 'MarkerFaceColor', 'green');
    xlabel('经度');
    ylabel('纬度');
    axis equal
    
    [num,txt,raw]=xlsread('provincial_ capital_coordinate12.xlsx');  %经纬度数据% 
     text(xDots(1)+0.2,yDots(1)+0.2,txt(1+1,2),'FontSize',9.5,'Color','red','FontWeight','Bold') ; %先画起点，突出起点
    for i=2:length-1
        text(xDots(i)+0.2,yDots(i)+0.2,txt(i+1,2),'FontSize',8,'Color','blue','FontWeight','Bold') ; %加上0.01使标号和点不重合，可以自己调整
    end
    
    
    
    hold on
    [minPathX,~] = find(totalDistances==minPath,1, 'first');
    bestPopPath = pop(minPathX, :);
    bestX = zeros(1,length);
    bestY = zeros(1,length);
    for j=1:length
       bestX(1,j) = cities(1,bestPopPath(1,j));
       bestY(1,j) = cities(2,bestPopPath(1,j));
    end
   % title('当前代数%d 的路径图');
    title(['第', num2str(gNumber),'代种群的最优路径图']) ;
    %行：再画城市的路径连线
    plot(bestX(1,:),bestY(1,:), 'red', 'LineWidth', 1.25);
    legend('城市', '路径');
    axis equal%行：axis equal/将横轴纵轴的定标系数设成相同值。
    grid on
    %text(5,0,sprintf('迭代次数: %d 总路径长度: %.2f',gNumber, minPath),'FontSize',10);
    drawnow
    hold off
end

最后感谢前人的博客，然我这个小白从0 完成了遗传算法的作业，也希望此博客能帮助到大家。

具体代码：https://download.csdn.net/download/qq_37271216/12089106

有需要代码的朋友也可以把邮箱留下，免费发到邮箱！