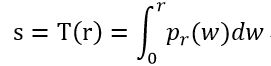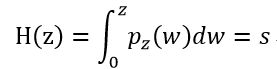直方图匹配

一、什么叫直方图匹配：

    规定处理后的图像的直方图形状，生成特定的直方图。

二、   直方图匹配的意义：

    当图像的灰度大部分集中在图像的暗端，直接进行直方图均衡会导致图像移向较高的一侧，从而产生一幅褪色的图像。而直方图匹配则能保留图像直方图的大体形状，使其不会被映射到较高端，从而使图像褪色。

三、直方图匹配的原理

    考虑归一化后在[0,1]区间内的连续灰度级，令r和z分别表示输入图像与输出图像的灰度级。输入图像灰度级有概率密度函数，输出图像的灰度级具有规定的概率密度函数。其变换为：

                                             

得到的灰度级s，它具有均匀的概率密度函数。现在假设我们定义变量z具有下列特性：

                                            

记住，我们要寻找的时灰度级为z的图像，且具有规定的概率密度函数。由前面两个等式可得：

                                                

我们可以由输入图像得到T(r)（即直方图均衡变换），得到结论：只要找到，就能利用前面的等式得到变换后的灰度级z，其概率密度函数函数（PDF）为规定的。当处理离散变量时，我们能够保证若是正确的直方图概率密度函数（即直方图具有单位面积且其各灰度值均为非负）时，H的反变换存在，且其元素值非零[即中没有容器是空的]。如同在直方图均衡中一样，前面方法的离散实现得到对特定直方图的近似。

四、实例

下面的函数计算一个归一化到单位区域的高斯函数，用其来作为特定指定的直方图。

function p = twomodegauss(m1,sig1,m2,sig2,A1,A2, k)
%计算一个归一化到单位区域的双模态高斯函数，它可被用做一个指定的直方图
c1 = A1 * (1 / ((2 * pi) ^ 0.5) * sig1);
k1 = 2*(sig1^2);
c2 = A2*(1 / ((2 * pi) ^ 0.5) * sig2);
k2 = 2*(sig2^2);
z = linspace(0,1,256);
p = k + c1 * exp(-((z - m1) .^ 2) ./ k1) + c2 * exp(-((z - m2) .^ 2) ./ k2) ;

p = p ./ sum(p(:));

function p = manualhist
%交互式函数从键盘读取输入信息，
%并绘制最终的高斯函数。
%函数input输出包含其参量的文字
%并等待来自用户的输入。
%一组比较好的初始数据为：（-0.85，0.05，0.75，0.05，1，

% 0.07,0.002）

%初始化
repeats = true;
quitnow = 'x';

%如果用户在估计至少一个直方图之前退出，则计算默认直方图
p = twomodegauss(0.15,0.05,0.75,0.05,1,0.07,0.002);

%一直循环直到x输入
while repeats
    s = input('Enter m1,sig1,m2,sig2,A1,A，k OR x to quit:','s');
    if strcmp(s,quitnow)
        break
    end
    
%将输入字符串转换为数值的向量并验证输入的数量 
    
    v = str2num(s);
    if numel(v) ~=7
        disp('Incorrect number of inputs.')
    end
    
    p = twomodegauss(v(1),v(2),v(3),v(4),v(5),v(6),v(7));
    %绘出新的图表，并且规定x坐标
    figure,plot(p)
    xlim([0 255])
end

>> I=imread('MoonPhotos.tif');
g=histeq(I,manualhist);            %进行直方图匹配并生成图像g
Enter m1,sig1,m2,sig2,A1,A，k OR x to quit:0.15 0.05 0.75 0.05 1 0.07 0.002

Enter m1,sig1,m2,sig2,A1,A，k OR x to quit:

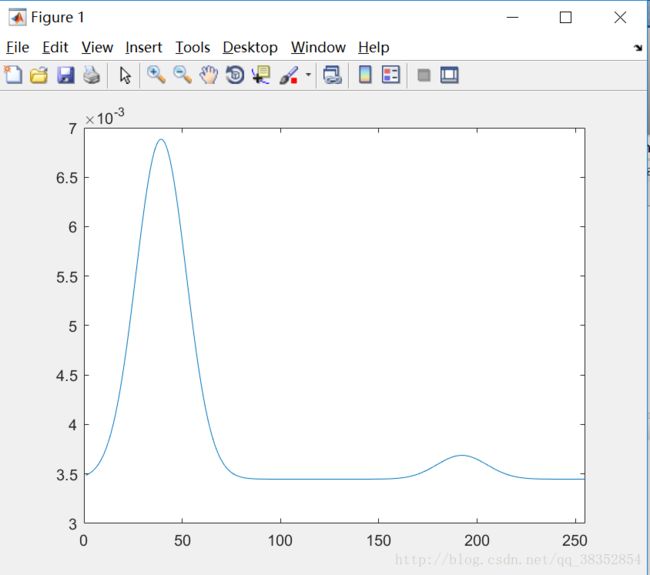
以下为manualhist函数生成的图像：

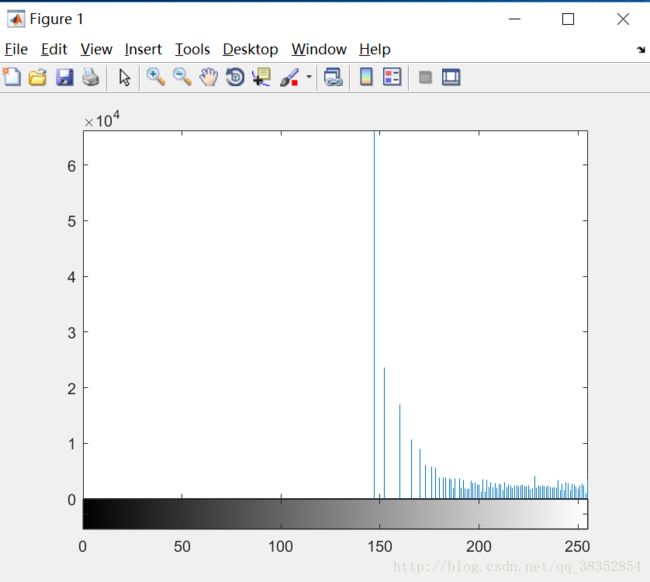
 figure,imhist(g)

以下为图像g的直方图

figure,imhist(I)

以下为原图I的直方图

    

    

     figure,imshow(I)

以下为原图像I：

    

    figure,imshow(g)

以下为直方图匹配后的图像：

在这里，利用直方图匹配改善了图像的视觉效果，相比直方图均衡，使得最低灰度级没有那么高。

当修改双模式高斯函数的参数时，将k=0.002变为0.02，结果如下：

 I=imread('MoonPhotos.tif');
g=histeq(I,manualhist);
Enter m1,sig1,m2,sig2,A1,A，k OR x to quit:0.15 0.05 0.75 0.05 1 0.07 0.02

Enter m1,sig1,m2,sig2,A1,A，k OR x to quit:x

以下为参数改为0.02时的双模高斯函数：

figure,imhist(g)

以下为进行了直方图匹配的图像的直方图：

 figure,imshow(I)

以下为原图像I的图像效果：

figure,imshow(g)

以下为进行了直方图匹配的图片：

注意：其中的特例是对比度受限的自适应直方图均衡。这种方法利用直方图匹配的方法来逐个处理图像中的较小区域（称为小片）。然后，使用双线性内插方法将相邻的小片组合起来，从而消除人工引入的边界。特别是均匀灰度区域，可以限制对比度来避免放大噪声。