二进制LDPC码的构造及译码算法

        构造好的LDPC码校验矩阵和设计性能优异的译码算法是LDPC码研究领域的重点。
       常见的LDPC码一般分为两类，一类是随机LDPC码，一般由随机化方法构造；另一类是准循环LDPC码，一般由半随机方

法或者基于代数的结构化方法构造。常见的LDPC码的迭代译码方法包括基于硬判决的译码和基于软判决的译码。接下来将介绍

几种具有代表性的LDPC码构造方法以及经典的硬判决和软判决译码方法。

1 . PEG构造和QC-PEG构造

        渐进边增长(progressive edge growth, PEG)算法[1][2][3]是一种著名的基于图的随机化LDPC码构造方法，其主要做法是依

次对每个变量节点添加边连接校验节点来构建出所要的Tanner图，在每次添加边的时候使当前变量节点的本地围长(当前变量节

点所参与的最短的环的长度)尽可能地大。这样虽然不能保证最终Tanner图对应的LDPC码是最优的，但是其性能一般也非常优

异。

     一个LDPC码的校验矩阵对应着唯一的一个Tanner图，PEG算法根据给定的码长、码率以及度分布，从头开始构建Tanner

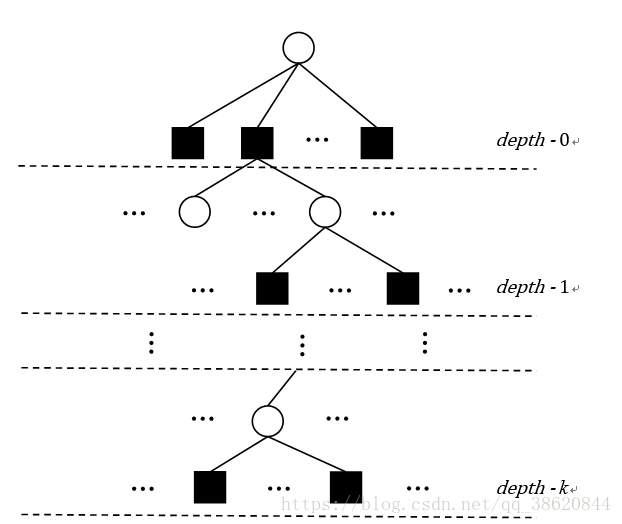
图。假设需要构建的Tanner图的校验节点数为m，变量节点数为n，变量节点vj相连的所有边所构成的集合记为，那么容易得

到所有的边的集合。记与vj相连的第k条边为，。以vj为根节点将Tanner图展开，把

在其展开的树上能达到l层的校验节点集合记为，与之相应的补集为，有，Nc为所有校验节点的集合。

其展开过程如下图1-1所示。

 

                               

                                                                             图1-1  k层树图展开

根据PEG算法[2][3]的思想，逐个地为每个变量节点选择合适的校验节点，然后在他们之间建立边，这里的索引从0开始，算法

的具体步骤描述如下：

1.1  选择一个变量节点vj(一般就按索引的顺序)。如果当前需要添加的是此节点的第0条边，则找到当前Tanner图中具有最低度

数的校验节点ci，将vj 和 ci 连起来就可得到此节点的第0条边。如果变量节点vj已经 添加过边，则首先以vj为根节点把当前

Tanner图展开为树图直到深度为l，如果发现 而，或者有集合中的校验节点不再继续增加但中的校验

节点的数目仍小于全体校验节点数m, 就在中选取度数最低的校验节点与vj相连。

 

1.2  重复步骤1.1)直到vj相连的边的条数等于所给定的vj的度数。

 

1.3  重复步骤1.1) 1.2)，直到所有变量节点的边都添加完毕。

       PEG算法构造的LDPC码能有效地减少短环的形成，但是其是一种随机化的构造方法，校验矩阵没有一定的结构和规律，

因而在硬件实现的时候需要耗费大量的空间和资源，不利于实际的应用；同时无规律的校验矩阵也不能实现快速编码，造成复

杂度高和效率低下。Li提出了可以构造准循环LDPC码的PEG算法[4]，要构造一个维数是m × n，子矩阵维数为L × L的准循环

LDPC校验矩阵，首先把变量节点和校验节点按每组L个节点进行分组，这样可以得到R组校验节点和C组变量节点，其中

R = m / L，C = n / L。在这个的基础上，Liu等人也做出了深入的研究，初步提出了一种基于PEG的伪随机构造算法[5]。经过深

入探讨与研究他们提出了一种构造准循环LDPC码的方法，该方法也结合了PEG算法，在保持准循环特性的基础上能够获得比

PEG算法更佳的译码性能，并且可以灵活地选择码长和码率[6]，这里称为QC-PEG算法, 其在添加边时将节点按顺序分组，每

组包含L个节点，只需要确定一组中的一个节点，那么其它节点所连接的边就可以通过循环移位的特性确定。

        QC-PEG引入一个称之为不可靠因数的系数β用来评估一个节点信息的可靠程度。一个节点的不可靠因数β值越大，表明该

节点的信息就越不可靠。很容易可以知道，一个节点的β值的大小和节点所参与的环的数目以及相应的环长的大小是密切相关

的。一个节点参与的环的数目越多，且长度越短，该节点的β值就越大，那么这个算法里给出的β值的计算方法就可以表示为

                                                                                                          (1-1)

其中，为第i个环的长度，k为该节点参与的环的个数。从节点的不可靠系数β出发，该算法还给出了一个环的不可靠因数α的定

义：α为组成该环所有节点的不可靠因数β之和。在选取合适的校验节点给当前变量节点vj连接新的边的过程中，如果在变量节

点vj和某个校验节点ci之间已经连接过了一条边，那么在校验节点集合Cd中的任何节点都不能和变量节点vj相连，这个集合称为与检验节点ci关联的受限节点集合，其中，每一个检验节点都有一个对应的

Cd。接下来，将以变量节点vj所在的关键列为例，具体阐述如何确定与vj相连的校验节点，其具体过程如下：

1. )为变量节点vj添加第一条边时，在当前已构建的Tanner图中寻找度数最小的校验节点ci，连接变量节点vj和校验节点ci这两个节点就可以得到第一条边。在添加变量节点vj的其它边时，以vj为节点将当前Tanner图展开到深度l，如果集合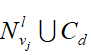包含节点数停止增长但仍然小于校验节点总数，则ci从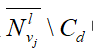中随机取一个后与vj相连。如果集合但是,则把校验节点集合定义为F1，如果F1中的校验节点的数目不唯一，那么执行步骤2)。
2. )考虑到vj添加的当前边也会对将添加的下一条边有影响，集合F1中不同的校验节点和vj相连时产生的当前短环和对vj添加下一条边也会产生影响。把F1中每一个校验节点与vj尝试相连，然后在此基础上再尝试对vj添加下一条边，不断尝试，直到选出F1中使得当前Tanner图形成的本地围长最大且短环数目最少的校验节点组成校验节点集合F2。
3. )在环不可避免的情况下，选取使得环的外信息度数最高的节点。找出校验节点集合F2中每个节点和vj相连时所形成的环，并计算这些环的外信息度数同时进行比较，将使得形成的环的外信息度数最小的校验节点放入一个新的集合F3。
4. )对于校验节点集合F3中的节点，搜索出F3中每个校验节点和vj相连时所形成的环，计算每个环的不可靠因数，然后从中选取使得最小的校验节点组成校验节点集合F4。最后从F4中任意选取一个校验节点和vj相连。

       对Tanner图对应校验矩阵中的所有关键列都进行以上的步骤，直到所有的关键列都确定，然后通过准循环性质就可以确定

整个Tanner图和校验矩阵了。

2. 基于代数方法的结构化构造

 

        准循环LDPC码更多地是以代数方法构造的[6][7][8]，一般都是基于有限域和矩阵论的，具有较强的理论性，虽然每个代数

构造方法略有不同，但基本原理是一致的，这里简述其一般过程。

       给定有限域GF(q)，为GF(q)的一个本原元，则本原元的幂次，即，给定了GF(q)上的q个元素。设P为一个大小为的循环置

换矩阵，其第0行为一个长度为取值在GF(2)上的向量(0,1,0,,0)，此向量的第1个元素为“1”，其它都是“0”。P的其它行都是上一

行的循环右移向量。P即由(0,1,0,,0)以及(0,1,0,,0)的(q – 2)个循环右移向量组成，为i个P的乘积，称为

P的i次幂，这里。也是一个大小为的循环置换矩阵，且其首行的向量的第i个元素为“1”。特别

地，即为单位阵。令，则(q – 1)个循环置换矩阵构成的集合构成了一个(q – 1)阶的GF(2)上的

矩阵乘法循环群，的乘法逆元为，为单位元。

       对，可用表示GF(q)的非零元，将映射为 的操作就是前面介绍过的矩阵的分散。与非零 之间有

一个一一对应的关系。GF(q)中的元素0则对应全零矩阵，记为。

      考虑GF(q)上 的基矩阵，

                       

      其行满足以下约束：对，任意两个q元n长序列 和之间的

Hamming距离至少为(n – 1)。这个约束称为行距 (row-distance, RD)约束，满足此约束的基矩阵W称为行距约束矩阵。通过将

基矩阵W中的各个GF(q)的元素映射为对应的循环置换矩阵，就能得到最终的的奇偶校验矩阵H。由满足

行距约束的W分散得到的H中不存在4环。H的零空间给定了一个长度为R(q – 1)，其码率至少为(R – C) / C。在文献[5]中，归纳

了几种满足行距约束的校验矩阵的构造方法，通过这些行距约束矩阵以及分散操作，可以构造得到几类常见的准循环LDPC码，

这里不再赘述。

 

 

• 参考文献

[1]  X. Y. Hu, E. Eleftheriou, and D. M. Arnold. Progressive edge-growth Tanner graphs [C]. IEEE Global Telecommunications Conference, San Antonio, TX, USA, Nov. 2001, 2: 995-1001.

[2]  X. Y. Hu, E. Eleftheriou, and D. M. Arnold. Regular and irregular Progressive edge-growth Tanner graphs [J]. IEEE Transactions on Information Theory, Jan. 2005, 51(1): 386-398.

[3]  Y. Fang, P. Chen, L. Wang, and F. C. M. Lau. Design of Protograph LDPC Codes for Partial Response Channels [J]. IEEE Transactions on Communications, Oct. 2012, 60(10): 2809-2819.

[4]  X. Liu, W. Zhang, and Z. Fan. Construction of quasi-cyclic ldpc codes and the performance on the pr4-equalized MRC channel [J]. IEEE Transactions on Magnetics, Oct. 2009, 45(10): 3699-3702.

[5] Y.-M. Lin, H.-T. Li, M.-H. Chung, and A.-Y. Wu. Byte-Reconfigurable LDPC Codes Design With Application to High-Performance ECC of NAND Flash Memory Systems [J]. IEEE Transactions on Circuits and Systems I: Regular Papers, July 2015, 62(7): 1794-1804.