matlab实现小波图像去噪
本文主要内容
1.简单置零操作实现小波域去噪
2.基于简单机器学习思想的小波去噪
下面是本次内容的全部代码
代码后面会有解释
如果你需要直接使用下面的代码,别忘了带走几个脚本中要调用到的函数
clc
clear
noiseAmp=2.1;%噪声的幅度
sourceImage=imread('colorWoman.jpg');%读取图片
noiseFreqCut=0.42;%高频噪声的截止频率
filterStep=3;%巴特沃斯滤波器的截止频率
waveletLayerNum=5;%小波的分层系数
waveletType='db3';%小波基的种类
exampleImageAmount=10;%样本图片的个数
exampleImageNameFormat='exampleImage';%样本图片的名字格式
%设置样本阈值参考度的相关变量
t=linspace(0,pi,waveletLayerNum);%曲线采样点
exampleReferAmpi=1+cos(t);%样本阈值参考度
gainDropRate=50*ones(1,waveletLayerNum);%映射曲线在阈值处增益的下降速率
sourceImageDouble=im2double(sourceImage);%改变数据类型,便于对图像的操作
sourceNoise=sqrt(noiseAmp)*randn(size(sourceImageDouble));%加在图像上的噪声
[mLength,nLength,channel]=size(sourceImageDouble);%获取图像的尺寸
%噪声通过高通滤波器
%制作高通滤波器
%获取图像的中心距离矩阵
[xAxis,yAxis]=dftuv(mLength,nLength);
%高通滤波器的频域表达式
highPassFilterH=1./(1+(((noiseFreqCut*nLength)^2)./(xAxis.^2+yAxis.^2)).^filterStep);
highFreqNoise=[];%存储高频噪声的滤波结果
for tempVar=1:channel%对噪声的每个颜色层分别操作
%取出一个单独的颜色层
oneLayerSourceNoise=sourceNoise(:,:,tempVar);
%单层图像通过高通滤波器
simpleLayerFilResult=dftfilt(oneLayerSourceNoise,highPassFilterH);
%卷积结果保存
highFreqNoise=cat(3,highFreqNoise,simpleLayerFilResult);
end
%将噪声和原始图像叠加
noisyImage=sourceImageDouble+highFreqNoise;
%原始图像、噪声图像、加噪图像小波系数的比较
%原始图像的小波系数
[sourceImageWaveComp,sourceImageWaveSize]=wavedec2(sourceImageDouble,waveletLayerNum,waveletType);
%噪声图像小波系数
[noiseWaveComp,noiseWaveSize]=wavedec2(highFreqNoise,waveletLayerNum,waveletType);
%加噪图像的小波系数
[noisyImageWaveComp,noisyImageWaveSize]=wavedec2(noisyImage,waveletLayerNum,waveletType);
%直接归零的噪声处理***************
%拷贝一分加噪图像的系数矩阵
simpleDenoiseWaveComp=noisyImageWaveComp;
%确定系数向量近似分量的长度
lengthAppWaveCoef=noisyImageWaveSize(1,1)*noisyImageWaveSize(1,2)*noisyImageWaveSize(1,3);
%确定第一层细节分量的长度
lengthDet1WaveCoef=noisyImageWaveSize(2,1)*noisyImageWaveSize(2,2)*noisyImageWaveSize(2,3)*3;
%确定第二层细节分量的长度
lengthDet2WaveCoef=noisyImageWaveSize(3,1)*noisyImageWaveSize(3,2)*noisyImageWaveSize(3,3)*3;
%保留第一、二层细节分量,后面的直接置零
simpleDenoiseWaveComp(lengthAppWaveCoef+lengthDet1WaveCoef+lengthDet2WaveCoef:length(noisyImageWaveComp))=0;
%恢复处理过的噪声小波系数
simpleDenoiseResult=waverec2(simpleDenoiseWaveComp,noisyImageWaveSize,waveletType);
%简单机器学习思想的尝试*******************
%若干无噪声向量的和
exampleCompVector=zeros(1,waveletLayerNum);
for tempVar=1:exampleImageAmount
%对应的图片名称
tempImageName=cat(2,exampleImageNameFormat,' (',int2str(tempVar),').jpg');
%无噪声系数向量的叠加
exampleCompVector=exampleCompVector+waveCompDetEsti(tempImageName,waveletLayerNum,waveletType);
end
%求若干无噪声系数向量的平均值
exampleCompVector=exampleCompVector/exampleImageAmount;
%标记系数矩阵中细节分量的位置
tempCompLocal=noisyImageWaveSize(1,1)*noisyImageWaveSize(1,2)*noisyImageWaveSize(1,3);
%记录系数向量的副本
mLearningWaveletResult=noisyImageWaveComp;
%遍历每一层细节系数矩阵
for tempVar=1:waveletLayerNum
%当前阶次细节分量向量的长度
tempCompLength=noisyImageWaveSize(1+tempVar,1)*noisyImageWaveSize(1+tempVar,2)*noisyImageWaveSize(1+tempVar,3)*3;
%对细节分量衰减
mLearningWaveletResult(tempCompLocal:tempCompLocal+tempCompLength)=waveletDenoiseGain(noisyImageWaveComp(tempCompLocal:tempCompLocal+tempCompLength),exampleReferAmpi(tempVar)*exampleCompVector(tempVar),gainDropRate(tempVar));
%更改系数矩阵位置
tempCompLocal=tempCompLocal+tempCompLength;
end
%恢复到图像
mLearningResult=waverec2(mLearningWaveletResult,noisyImageWaveSize,waveletType);
%结果显示****************
%原始图像
figure
imshow(sourceImage);
title('原始图像');
%原始噪声
figure
imshow(sourceNoise+0.5);
title('原始噪声')
%高频噪声
figure
imshow(highFreqNoise+0.5);
title('高频噪声')
%带有噪声的图像
figure
imshow(noisyImage);
title('带有噪声的图像')
%原始图像的小波系数
figure
plot(sourceImageWaveComp);
title('原始图像的小波系数')
%噪声图像的小波系数
figure
plot(noiseWaveComp)
title('噪声图像的小波系数')
%加噪图像的小波系数
figure
plot(noisyImageWaveComp)
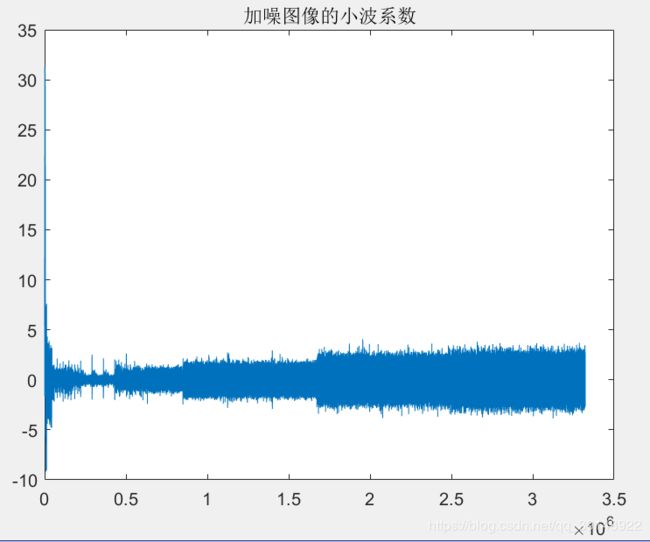
title('加噪图像的小波系数')
%简单归零处理的图像结果
figure
imshow(simpleDenoiseResult)
title('简单归零处理的图像结果')
%原始小波系数和噪声图像的小波系数的比较
figure
plot(noisyImageWaveComp);
hold on
plot(sourceImageWaveComp);
title('原始图像和噪声图像小波系数的比较');
%用于参考的无噪声系数向量
figure
stem(exampleCompVector)
title('样本系数向量')
%加噪小波系数经过衰减处理后
figure
plot(mLearningWaveletResult);
title('加噪小波系数经过衰减处理后');
%简单学习去噪结果和原始图像比较
figure
plot(mLearningWaveletResult);
hold on
plot(sourceImageWaveComp)
title('原始图像小波系数和去噪结果比较')
%简单机器学习算法去噪结果
figure
imshow(mLearningResult)
title('简单机器学习算法去噪结果')
脚本参数部分
noiseAmp=2.1;%噪声的幅度
sourceImage=imread('colorWoman.jpg');%读取图片
noiseFreqCut=0.42;%高频噪声的截止频率
filterStep=3;%巴特沃斯滤波器的截止频率
waveletLayerNum=5;%小波的分层系数
waveletType='db3';%小波基的种类
exampleImageAmount=10;%样本图片的个数
exampleImageNameFormat='exampleImage';%样本图片的名字格式
%设置样本阈值参考度的相关变量
t=linspace(0,pi,waveletLayerNum);%曲线采样点
exampleReferAmpi=1+cos(t);%样本阈值参考度
gainDropRate=50*ones(1,waveletLayerNum);%映射曲线在阈值处增益的下降速率参数集中给出是为了方便参数的随时改变,在算法性能调试的时候是极大优化coding体验的环节
有些参数现在可能还不明白用途,到后面使用到这些参数的时候自然就会知道。
参数的初步处理
sourceImageDouble=im2double(sourceImage);%改变数据类型,便于对图像的操作
sourceNoise=sqrt(noiseAmp)*randn(size(sourceImageDouble));%加在图像上的噪声
[mLength,nLength,channel]=size(sourceImageDouble);%获取图像的尺寸关于im2double可参考https://blog.csdn.net/qq_39148922/article/details/84720710
sourceNoise是用来加在图片上的噪声,前面参数列表中的幅度其实就是正态分布的标准差
高频噪声的制作
%制作高通滤波器
%获取图像的中心距离矩阵
[xAxis,yAxis]=dftuv(mLength,nLength);
%高通滤波器的频域表达式
highPassFilterH=1./(1+(((noiseFreqCut*nLength)^2)./(xAxis.^2+yAxis.^2)).^filterStep);
highFreqNoise=[];%存储高频噪声的滤波结果
for tempVar=1:channel%对噪声的每个颜色层分别操作
%取出一个单独的颜色层
oneLayerSourceNoise=sourceNoise(:,:,tempVar);
%单层图像通过高通滤波器
simpleLayerFilResult=dftfilt(oneLayerSourceNoise,highPassFilterH);
%卷积结果保存
highFreqNoise=cat(3,highFreqNoise,simpleLayerFilResult);
end
%将噪声和原始图像叠加
noisyImage=sourceImageDouble+highFreqNoise;图像中由外界因素干扰形成的噪声通常是高频噪声
数字图像中频率的概念和一些粗浅的解释可以参考
https://blog.csdn.net/qq_39148922/article/details/86588538
高频噪声制作方法的解释可参考
https://blog.csdn.net/qq_39148922/article/details/86608491
接下来对原始图像、噪声图像和加噪图像进行小波系数分解
%原始图像、噪声图像、加噪图像小波系数的比较
%原始图像的小波系数
[sourceImageWaveComp,sourceImageWaveSize]=wavedec2(sourceImageDouble,waveletLayerNum,waveletType);
%噪声图像小波系数
[noiseWaveComp,noiseWaveSize]=wavedec2(highFreqNoise,waveletLayerNum,waveletType);
%加噪图像的小波系数
[noisyImageWaveComp,noisyImageWaveSize]=wavedec2(noisyImage,waveletLayerNum,waveletType);即使你完全对小波没有概念,也可以通过小波系数分解结果中看出一些去噪的方法
你看——
它们三个的第一个返回值的区别
比较发现,小波系数的“包络”:
噪声的小波系数整体呈现台阶状上升
无噪声的原始图像的小波系数 在最开始的一小部分呈现台阶状下降,后期系数趋近于零,而且存在某种模糊的周期性
加了噪声的小波系数在刚开始的下降台阶部分和原始图像的小波系数基本上相同,到后期的小波系数主要与噪声图像的小波系数相似。所以小波系数靠后的部分“被噪声淹没”,前面的部分却大部分保留了下来
所以即使不了解小波,也可以想到,把加噪图像的小波系数后面的“上升台阶”部分直接置零
也可以达到一种比较可观的去噪效果
代码中提到的第一种方法用的就是这种思想,但是并没有直接这样做
%直接归零的噪声处理***************
%拷贝一分加噪图像的系数矩阵
simpleDenoiseWaveComp=noisyImageWaveComp;
%确定系数向量近似分量的长度
lengthAppWaveCoef=noisyImageWaveSize(1,1)*noisyImageWaveSize(1,2)*noisyImageWaveSize(1,3);
%确定第一层细节分量的长度
lengthDet1WaveCoef=noisyImageWaveSize(2,1)*noisyImageWaveSize(2,2)*noisyImageWaveSize(2,3)*3;
%确定第二层细节分量的长度
lengthDet2WaveCoef=noisyImageWaveSize(3,1)*noisyImageWaveSize(3,2)*noisyImageWaveSize(3,3)*3;
%保留第一、二层细节分量,后面的直接置零
simpleDenoiseWaveComp(lengthAppWaveCoef+lengthDet1WaveCoef+lengthDet2WaveCoef:length(noisyImageWaveComp))=0;
%恢复处理过的噪声小波系数
simpleDenoiseResult=waverec2(simpleDenoiseWaveComp,noisyImageWaveSize,waveletType);利用wavedec2的第二个返回值来判断第一层和第二层细节分量的位置,把它们保留下来,后面的置零,从而得到的去噪效果如下(这种方法通常只在分解的层数比较少的时候才管用)
其实简单归零处理结果仍然有瑕疵,可以自行运行代码体验
下面介绍基于简单机器学习算法的小波图像去噪
(这里说是“简单机器学习算法”只是个人的一厢情愿,其实只是对若干无噪声图像进行小波分解,从而确定一个参考的阈值而已)
%简单机器学习思想的尝试*******************
%若干无噪声向量的和
exampleCompVector=zeros(1,waveletLayerNum);
for tempVar=1:exampleImageAmount
%对应的图片名称
tempImageName=cat(2,exampleImageNameFormat,' (',int2str(tempVar),').jpg');
%无噪声系数向量的叠加
exampleCompVector=exampleCompVector+waveCompDetEsti(tempImageName,waveletLayerNum,waveletType);
end
%求若干无噪声系数向量的平均值
exampleCompVector=exampleCompVector/exampleImageAmount;
%标记系数矩阵中细节分量的位置
tempCompLocal=noisyImageWaveSize(1,1)*noisyImageWaveSize(1,2)*noisyImageWaveSize(1,3);
%记录系数向量的副本
mLearningWaveletResult=noisyImageWaveComp;
%遍历每一层细节系数矩阵
for tempVar=1:waveletLayerNum
%当前阶次细节分量向量的长度
tempCompLength=noisyImageWaveSize(1+tempVar,1)*noisyImageWaveSize(1+tempVar,2)*noisyImageWaveSize(1+tempVar,3)*3;
%对细节分量衰减
mLearningWaveletResult(tempCompLocal:tempCompLocal+tempCompLength)=waveletDenoiseGain(noisyImageWaveComp(tempCompLocal:tempCompLocal+tempCompLength),exampleReferAmpi(tempVar)*exampleCompVector(tempVar),gainDropRate(tempVar));
%更改系数矩阵位置
tempCompLocal=tempCompLocal+tempCompLength;
end
%恢复到图像
mLearningResult=waverec2(mLearningWaveletResult,noisyImageWaveSize,waveletType);分别读取参考图像的小波分解系数,加到存储向量里面,最后求平均值
需要说一下的是,代码最开始的参数里面有一个
exampleImageNameFormat='exampleImage';%样本图片的名字格式
运行代码的时候需要先把样本图片放在和脚本相同的目录下,全部选中,然后按下“F2"键,对图片命名为"exampleImage"
这样就可以比较方便地在循环中确定要参考的图片的名称
这里会用到一个调用函数,为个人临时所写 waveCompDetEsti
代码如下:
function [detMaxVector] = waveCompDetEsti(imageName,layerNum,waveletType)
%UNTITLED 返回一个向量,向量中依次是各个阶次细节分量的绝对值的最大值
% 图片名称的字符表示,小波分解的层数,小波基的种类
%读取输入的图片
imageMar=im2double(imread(imageName));
%对输入的图片进行小波系数分解
[waveComp,waveSize]=wavedec2(imageMar,layerNum,waveletType);
%分别求小波系数记录最大值
detMaxVector=[];
for tempVar=1:layerNum
detVector=[detcoef2('h',waveComp,waveSize,tempVar),detcoef2('v',waveComp,waveSize,tempVar),detcoef2('d',waveComp,waveSize,tempVar)];
detMaxVector=cat(2,max(max(max(abs(detVector)))),detMaxVector);
end
end
它依次确定了参考图像每一层细节分量的最大值,最后求几个图像最大值的平均值
最终确定的参考阈值为(以7阶为例):
之后要对加噪图像的每一层细节分量进行阈值处理
阈值处理函数为个人临时所写,代码如下:
function [result] = waveletDenoiseGain(operateVar,dropLocal,dropRate)
%UNTITLED 用于小波图像去噪的细节分量系数映射
% 用反正切函数映射
%保留符号
result=-atan(dropRate*(abs(operateVar)-dropLocal))/pi+0.5;
result=operateVar.*result;
end
阈值处理使用的是经过平移缩放的反正切函数,图形如下
该图为阈值为5的一个阈值处理函数,图中表示的含义为处理前到处理后的映射
上面提到,用参考图像获得的参考阈值是图像的各层小波系数的最大值,但最佳阈值不一定是最大值,所以需要在前面有一个调整系数
而且高层的小波系数(系数向量中靠前的部分)包含的图像信息更多,参考价值应该更大,低层的小波系数参考价值应该较小。
为了满足这种要求,个人经过一番探索,最后发现用余弦函数【1+cos】可以比较好地完成去噪的功能,大家也可以自行尝试其它的参考系数向量,也就是代码最上面的参数列表的这一行:
t=linspace(0,pi,waveletLayerNum);%曲线采样点
exampleReferAmpi=1+cos(t);%样本阈值参考度
同时阈值处理下降速率与阈值截止部分的锐利性有关,也可自行调整
7阶的时候去噪结果如下:
和原图还是有一些差距,欢迎交流指正。