大学物理实验绪论笔记——关于物理实验的误差分析、处理与数据记录

一、完整的测量结果表达式举例

以钢丝的杨氏模量为例：

测量结果为：E=(1.89±0.08)x (N/m2)

                 或 E=1.89x(1±4.3%)  (N/m2)

应包括：测量量（代表符号）+测量量值+不确定度+测量值的单位

二、测量

直接测量：所要测量的量不必将实测的量经过任何函数关系的计算而直接得到

间接测量：通过欲测量的量与直接实测的量之间已知的函数关系，经过计算得到欲测量的量的值

三、误差

定义：测量值-真实值

分类：系统误差、随机误差

表示：绝对误差、相对误差

系统误差：在对同一被测量的多次测量过程中，绝对值和符号保持恒定或以可预知的方式变化的误差分量

               误差原因：测量仪器、测量方法、环境等

随机误差：对同一量的多次重复测量中，每次测量值相对于真值有一个无规律的涨落（大小、方向）的误差分量

                误差特点：多次测量时分布对称，具有抵偿性——因此取多次测量的平均值有利于消减随机误差

随机变量的统计规律——正态分布（Gauss分布）：

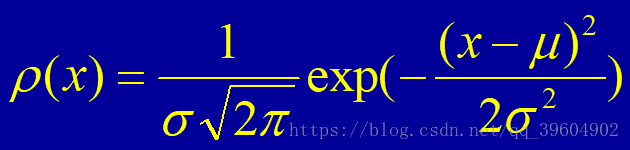在对同一被测量的多次测量过程中，绝对值和符号保持恒定或以可预知的方式变化的测量误差的分量。

（标准差）决定线形的宽窄，表征测量值的分散程度

 （数学期望值）

测量值落在【μ-σ，μ+σ】区间的概率是68.3%；若把区间范围扩大到【μ-2σ，μ+2σ】，则测量值落到此区域的概率是95.4%；落在【μ-σ，μ+σ】区间的概率是99.7%

绝对误差：测量结果-被测量的真值

相对误差：E = 被测量的绝对误差/被测量的真值（用百分数表示）

四、测量不确定度

理解：不确定度表示由于测量误差存在而对被测量值不能确定的程度。不确定度是一定概率下的误差限值

不确定度反应了可能存在的误差分布范围，即随机误差分量和未定系统误差的联合分布范围

形式：总是不为零的正值，可以具体评定（但误差一般是不能计算的）

（1）已定系统误差：例如电表、读数显微镜的零位误差等，此项必须修正

（2）未定系统误差：已知存在于某个范围，而不知具体数值的系统误差，例如游标卡尺的允差

总不确定度分为两类不确定度：

           A类分量 ——多次重复测量时与随机误差有关的分量；

           B类分量 ——与未定系统误差有关的分量；

           这两类分量在相同置信概率下用方和根方法合成总不确定度：

           

具体使用中，测量不确定度有三种不同的表述：

（1）直接测量的合成标准不确定度

（2）间接测量的合成标准不确定度

（3）扩展不确定度

1. 直接测量的合成标准不确定度估算

A类评定：可用统计方法评定的不确定度部分

B类评定：要用其他方法评定的不确定度部分

估算过程：

• 求测量数据列的平均值          
• 用贝赛儿公式求标准偏差s           
• 平均值的标准偏差是上式一列测量中单次测量的标准偏差S的    
• 当 5＜n≤10，置信概率为95%时，可简化认为  
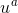
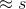
• 根据使用仪器得出 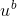 = Δ仪
• 由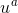、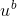合成总不确定度 u
• 给出直接测量的最后结果 y =  u

2. 间接测量的合成标准不确定度

用诸不确定度u()代替微分d,有：

   适用于和差形式的函数

  适用于积商形式的函数

   

五、有效数字表示法及运算规则

作为一个通用规定，测量值只能写到也应该写到开始有误差的哪一位到两位。其后的数字按“四舍六进五凑双”法则（即，后面的数字是四及以下就舍掉，是六及以上就进一，遇五若前面是奇数就进一，最后以为就变成是偶数，若前面已是偶数，则舍掉取舍”）

有效数字的位数多少直接反映测量的精确度。有效位数越多，表明测量的准确度越高

有效数值的位数与小数点位置无关，也不因使用的单位不同而改变

在运算过程中的有效数字取舍，一般遵循：加减运算的结果以参与运算的末位最高的数为准；乘除则以有效数字最少的数为准，有时可比其多取一位

例如： 12.4+0.571=13.0;    3600x8=2.9x

数值书写要求：

1. 有效数字的位数由合成不确定度来确定。测定值的最后一位与不确定度的最后一位对齐。一般的，不确定度只取一位或二位，不可多取。

2. 为方便起见，对较大或较小的数值，常采用科学记数法。

有效数字应用举例：

1)6.6006.0=1.1

2)(6788+67.88)x2.0=1.4×

3)(4400000±2000)m的正确表达式

        （440.0±0.2)×m

4)  ×3=5×

六、数据处理：

1. 列表

2. 逐差法

在有些实验中，我们连续取得一些数据。如果依次相减，就会发现中间许多数据并未发挥作用，而影响到实验的可靠性。

这种处理数据的方法称为逐差法。此法的优点是充分利用所测的数据，有利于减少测量的随机误差和仪器带来的误差。是实验中常用的处理数据的方法。

3. 作图法

（1）图示法：用图形曲线来表达物理量的变化

（2）图解法：用作图的方法来寻求两个物理测量量的解析关系

4. 数据的直线拟合（最小二乘法）

y =f(x)=a+bx

   

r为相关系数，表示两个变量之间的函数关系与线形的符合程度，r [-1，1]。|r|1，x、y 间线性关系好， |r|0 ，x、y 间无线性关系，拟合无意义。

物理实验中一般要求 r 绝对值达到0.999以上(3个9以上) 。

a, b, r 的具体求解方法：二维统计功能计算器，excel，编程求解