数据结构：简单算数表达式二叉树的构建和求值

内容：编写一个程序，先用二叉树来表示一个简单算术表达式，树的每一个结点包括一个运算符或者运算数。在简单算术表达式中只含+，-，*，/ 和一位正整数且格式正确（不包含括号），并且要先按照先乘除后加减的原则构造二叉树，然后由对应的二叉树计算该表达式的值。
解：

这里用非递归算法，根据对简单算数表达式的观察，如1+2*3-4/5 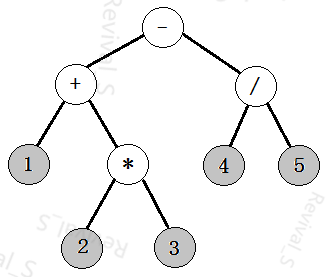 ，同一棵子树中+、- 号一定在*，/ 号的上层，而且在表达式中如果直接单独观察+-的两边，如：1 + 2*3，2*3 - 4/5。会发现+-的两侧子树要么为数字节点，要么为*/节点。于是不妨以加减法为分界线(因为会先计算乘除法)将表达式分割成若干个加减项后再将已生成的加减项节点（如2*3*4，8，3/2等）与加减符号项节点提取出来。则每个加减项节点（如2*3*4，8，3/2等）都是一棵棵小树（子树），将这些小树再由+-加减符号项为根节点依次连接成一棵"大树"就构成了题目要求的二叉树。

在生成小数的过程中，可由表达式字符串，循环，逐字符读取

若为数字

        新建节点p，将数字放入p->data，并且p左右孩子置空。

若为+-

        将前一个节点p放入事先准备好的一个存放加减项的数组中，存放既证明这个加减项已经构造完毕，然后再将+-符号新建个节点放入另一个数组中。循环结束后依次将此两个数组中的节点相互串接起来形成二叉树即可。

若为*，/

        则一定是构造成 数字 * 数字，的一棵小树的形式，而前一个数字已经读取，既为p节点，可由*/符号新建为根节点后，根节点的左孩子接上p，根节点的右孩子接上下一个字符的节点（下一个字符必为数字）。注意因为我们已经读取了当前字符的下一个字符，则此时循环中逐字符读取的计数器要+1一次，以防下次循环再次读到这个字符。

然后，重点，将p指向此时的根节点（既字符为*/ 的节点），这样进入下个循环后，若为*/，则可以将此p节点当做左子树继续接入*/为根的树中。若为+-，则此p做为一个构造完整的加减项存入数组。

最后将最后一个p放入加减项数组即可。然后就是串接两数组节点的工作了。

具体代码如下（C语言）

#include
#include
#include

typedef struct BTreeNode
{
	char data;
	struct BTreeNode* lchild;
	struct BTreeNode* rchild;
} BTNode;

int calcula(BTNode* T)
{
	if(T==NULL)
		return 0;
	if(T->data <='9'&&T->data >='0')
		return (T->data-'0');
	else
	{
		switch(T->data)            //因为这一步的T->data必为运算符，则必有左右孩子节点且不空
		{
     		case'+':  return calcula(T->lchild) + calcula(T->rchild); break;
			case'-':  return calcula(T->lchild) - calcula(T->rchild); break;
			case'*':  return calcula(T->lchild) * calcula(T->rchild); break;
			case'/':  return calcula(T->lchild) / calcula(T->rchild); break;
		}
	}
}

char* input_cheak_str()            //字符串动态输入与检测函数
{
	printf("请输入一个简单算术表达式(一位正整数且只有+-*/无括号,输入空格结束):\n");
	int ch_num=0;
	char ch,*str;
	str=(char*)malloc(sizeof(char));
	while((ch=getchar())!='\n')    //设置按照输入字符数变化的字符数组(内存足够则不受数组长度影响)
	{
		if(ch_num%2==1)            //下标为奇数，字符应为运算符号
		{
			if(ch!='+' && ch!='-' && ch!='*' && ch!='/')
			{
				printf("第%d个字符输入不合法!应为“+-*/”之一",ch_num+1);
				return '\0';
			}
		}
		else                       //下标为偶数，字符应为数字
		{
			if(!(ch>='0' && ch<='9'))
			{
				printf("第%d个字符输入不合法!应为0至9数字之一",ch_num+1);
				return '\0';
			}
		}
		str[ch_num]=ch;
		str=(char*)realloc(str,(++ch_num+1)*sizeof(char));   //∵ch_num为字符数组下标,而realloc参数为字符个数
	}                                                        //∴新开数组长度参数为下标+2,相当于参数为num++后的num+1
	if(str[ch_num-1]=='+' || str[ch_num-1]=='-' || str[ch_num-1]=='*' || str[ch_num-1]=='/')
	{                                                        //若最后一个字符为运算符则输入不合法
		printf("最后一个字符输入不合法!应为数字!",ch_num+1);
		return '\0';
	}
	str[ch_num]='\0';    //串结尾设置串结束符
	return str;
}

/*构建二叉树算法主体思路是将正确(输入时经过检测)的一位正整数无括号的简单表达式字符串，以加减法为分界线(因为会先计算乘除法)
将表达式分割成若干个加减项后再将已生成的加减项节点与加减符号项节点交替连接成树，其中每个加减项节点都是其子树。
*/

//本可以用数组表示指针数组ASItem,ASSign,因编译器不支持C99故无法用变量定义数组长,故只能用二级指针和malloc构造指针数组
BTNode* creat_tree(char *str)
{
	int itemCount=0,ASCount=0,len=strlen(str),i; //AS意为addSub加减法,前者为加减项计数,后者为加减符号计数,用于数组下标
	BTNode **ASItem,**ASSign,*root,*p;           //ASItem指针数组存放加减项节点指针,ASSign指针数组存放加减符号节点指针
	ASItem=(BTNode**)malloc((len/2+1)*sizeof(BTNode*));
	ASSign=(BTNode**)malloc((len/2)*sizeof(BTNode*)); 
	if(str[0]=='\0')                             //加减符号节点数必为加减项节点数+1.既itemCount==ASCount+1
		return NULL;
	for(i=0;i='0')
		{
			p=(BTNode*)malloc(sizeof(BTNode));
			p->data=str[i];
			p->lchild=p->rchild=NULL;
		}
		else if(str[i]=='+'||str[i]=='-')
		{
			ASItem[itemCount++]=p;     //将p节点放入加减项数组
			p=(BTNode*)malloc(sizeof(BTNode));
			p->data=str[i];
			ASSign[ASCount++]=p;
		}   //将加减符号节点指针放入ASSign数组,因有符号节点的孩子必不为空且创建过程不会访问其孩子节点,故无需置空
		else                           //str[i]符号为乘除的情况
		{
			root=(BTNode*)malloc(sizeof(BTNode));
			root->data=str[i];         //将*,/作为数据存入根节点数据域
			root->lchild=p;            //p一定为数字或*,/节点(都是已构造好的)
			p=(BTNode*)malloc(sizeof(BTNode));
			p->data=str[++i];          //此时p为当前节点的下一个节点,此时str[++i]必为数字,且下一个访问的str必为符号
			p->lchild=p->rchild=NULL;
			root->rchild=p;            //根节点的右孩子连上此节点
			p=root;                    //整个根节点构造完毕，传入p
		}
	}
	ASItem[itemCount]=p;
	ASSign[0]->lchild=ASItem[0];       //第一个符号节点左孩子连第一个项节点
	ASSign[0]->rchild=ASItem[1];
	for(i=1;ilchild=ASSign[i-1]; //除第一个节点以外的加减符号节点左孩子都连上一个符号节点
		ASSign[i]->rchild=ASItem[i+1]; //右孩子都连项节点
	}
	return ASSign[ASCount-1];
}

int main ()
{
	printf("%d\n",calcula(creat_tree(input_cheak_str())));
	return 0;
}

运行结果（这里由构造二叉树，然后二叉树计算直接列出出结果了，读者可自行选择添加输出二叉树函数）