【机器学习系列】之sklearn实现SVM代码
作者:張張張張
github地址:https://github.com/zhanghekai
【转载请注明出处,谢谢!】
【机器学习系列】之SVM硬间隔和软间隔
【机器学习系列】之SVM核函数和SMO算法
【机器学习系列】之支持向量回归SVR
【机器学习系列】之sklearn实现SVM代码
文章目录
- 一、sklearn实现线性可分SVM分类
- 二、sklearn实现线性不可分SVM分类
- 三、sklearn实现SVM非线性分类
一、sklearn实现线性可分SVM分类
import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm
%matplotlib inline
加载数据
def loadDataSet():
dataMat = [[3.542485,1.977398],
[3.018896,2.556416],
[7.551510,-1.580030],
[2.114999,-0.004466],
[8.127113,1.274372]]
labelMat = [-1,-1,1,-1,1]
return dataMat,labelMat
为样本和类别赋值
X,Y = loadDataSet()
X = np.mat(X)
拟合一个SVM模型
clf = svm.SVC(kernel='linear')
clf.fit(X,Y)
SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0,
decision_function_shape='ovr', degree=3, gamma='auto_deprecated',
kernel='linear', max_iter=-1, probability=False, random_state=None,
shrinking=True, tol=0.001, verbose=False)
获得支持向量
如果是二分类任务的话,第一个支持向量和最后一个支持向量肯定为不同的类别。
clf.support_vectors_
array([[ 3.542485, 1.977398],
[ 7.55151 , -1.58003 ],
[ 8.127113, 1.274372]])
获得支持向量的索引
clf.support_
array([0, 2, 4])
为每一个类别获得支持向量的数量
clf.n_support_
array([1, 2])
获取分割超平面法向量值
w = clf.coef_[0]
print(w)
[ 0.42314995 -0.0853665 ]
常数项 b
b = clf.intercept_[0]
print(b)
-2.3302333935392263
在指定区间返回50个均匀间隔的数字
为画图做准备,此步骤可理解为设置x轴坐标间隔和范围,
主要目的是为了画“支持向量线”和“超平面分隔线”,
因为划线时a*x+b除了上述计算出的a和b外,还需知道x的值,
这里x的取值对模型无影响,可取任意值(只对画出的图是否好看有影响)
xx = np.linspace(-2,10)
print(xx)
[-2. -1.75510204 -1.51020408 -1.26530612 -1.02040816 -0.7755102
-0.53061224 -0.28571429 -0.04081633 0.20408163 0.44897959 0.69387755
0.93877551 1.18367347 1.42857143 1.67346939 1.91836735 2.16326531
2.40816327 2.65306122 2.89795918 3.14285714 3.3877551 3.63265306
3.87755102 4.12244898 4.36734694 4.6122449 4.85714286 5.10204082
5.34693878 5.59183673 5.83673469 6.08163265 6.32653061 6.57142857
6.81632653 7.06122449 7.30612245 7.55102041 7.79591837 8.04081633
8.28571429 8.53061224 8.7755102 9.02040816 9.26530612 9.51020408
9.75510204 10. ]
二维直线方程
w ∗ x + b = 0 ⟹ w 1 x 1 + w 2 x 2 + b = 0 ⟹ x 2 = − w 1 x 1 + b w 2 w*x+b = 0\implies w_1x_1 + w_2x_2 +b = 0\implies x_2 = -\frac{w_1x_1+b}{w_2} w∗x+b=0⟹w1x1+w2x2+b=0⟹x2=−w2w1x1+b
这里的 x 1 、 2 x_1、_2 x1、2为数据集不同维度上的数值;
下述 x x xx xx和 y y yy yy分别代表两个维度上的值。
yy = -(w[0] * xx + b) / w[1] # 根据一个维度的值可以计算出另一个维度的值
print(yy)
[-37.21053572 -35.9966104 -34.78268508 -33.56875975 -32.35483443
-31.14090911 -29.92698379 -28.71305846 -27.49913314 -26.28520782
-25.0712825 -23.85735717 -22.64343185 -21.42950653 -20.21558121
-19.00165588 -17.78773056 -16.57380524 -15.35987992 -14.1459546
-12.93202927 -11.71810395 -10.50417863 -9.29025331 -8.07632798
-6.86240266 -5.64847734 -4.43455202 -3.22062669 -2.00670137
-0.79277605 0.42114927 1.6350746 2.84899992 4.06292524
5.27685056 6.49077589 7.70470121 8.91862653 10.13255185
11.34647718 12.5604025 13.77432782 14.98825314 16.20217846
17.41610379 18.63002911 19.84395443 21.05787975 22.27180508]
通过支持向量绘制分割超平面
-
已知一点 ( x 0 , y 0 ) (x_0,y_0) (x0,y0)和斜率 a a a,求该直线方程: y − y 0 = a ( x − x 0 ) y-y_0=a(x-x_0) y−y0=a(x−x0)
-
已知直线的法向量为 n = ( m , b ) n=(m,b) n=(m,b),则直线的斜率为: a = − m b a = -\frac{m}{b} a=−bm
# 直线斜率
a = -w[0] / w[1]
# 选择第一个类别的支持向量,并计算y值
x_1 = clf.support_vectors_[0]
yy_dowm = a * (xx - x_1[0]) + x_1[1]
# 选择另一个类别的支持向量,并计算y值
x_2 = clf.support_vectors_[-1]
yy_up = a * (xx - x_2[0]) + x_2[1]
绘制模型示意图
# 绘制超平面及支持向量
plt.plot(xx, yy, 'r-')
plt.plot(xx, yy_dowm, 'k--')
plt.plot(xx, yy_up, 'k--')
# 将数据集上的点绘制到模型图中
plt.scatter([X[:, 0]], [X[:, 1]], c='b', s=80, cmap=plt.cm.Paired)
# 绘制支持向量上的点
plt.scatter(clf.support_vectors_[:,0], clf.support_vectors_[:,1], s=80, c='g')
plt.show()
效果展示

其中:绿色点为支持向量,绿色+蓝色点为该数据集中所有样本点。
进行预测
clf.predict([[1, 1]])
array([-1])
clf.predict([[6, -5]])
array([1])
二、sklearn实现线性不可分SVM分类
import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm
%matplotlib inline
加载数据
此数据可以在我的github中获取。
def loadDataSet(fileName):
"""loadDataSet(对文件进行逐行解析,从而得到第行的类标签和整个数据矩阵)
Args:
fileName 文件名
Returns:
dataMat 数据矩阵
labelMat 类标签
"""
dataMat = []
labelMat = []
fr = open(fileName)
for line in fr.readlines():
lineArr = line.strip().split('\t')
dataMat.append([float(lineArr[0]), float(lineArr[1])])
labelMat.append(float(lineArr[2]))
return dataMat, labelMat
为样本和类别赋值
X,Y = loadDataSet('G:\\desktop\\svmdata线性不可分 .txt')
X = np.mat(X)
拟合一个SVM模型
clf = svm.SVC(kernel='linear')
clf.fit(X,Y)
SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0,
decision_function_shape='ovr', degree=3, gamma='auto_deprecated',
kernel='linear', max_iter=-1, probability=False, random_state=None,
shrinking=True, tol=0.001, verbose=False)
获得支持向量
如果是二分类任务的话,第一个支持向量和最后一个支持向量肯定为不同的类别。
clf.support_vectors_
array([[ 3.125951, 0.293251],
[ 4.658191, 3.507396],
[ 3.023938, -0.057392],
[ 5.286862, -2.358286],
[ 6.080573, 0.418886],
[ 2.912122, -0.202359],
[ 3.223038, -0.552392],
[ 3.457096, -0.082216],
[ 6.960661, -0.245353],
[ 2.893743, -1.643468],
[ 6.543888, 0.433164]])
获得支持向量的索引
clf.support_
array([10, 17, 30, 54, 55, 97, 23, 29, 46, 52, 69])
为每一个类别获得支持向量的数量
clf.n_support_
array([6, 5])
获取分割超平面法向量值
w = clf.coef_[0]
print(w)
[ 0.48860878 -0.23292803]
常数项 b
b = clf.intercept_[0]
print(b)
-2.4587710972338503
在指定区间返回50个均匀间隔的数字
为画图做准备,此步骤可理解为设置x轴坐标间隔和范围,
主要目的是为了画“支持向量线”和“超平面分隔线”,
因为划线时a*x+b除了上述计算出的a和b外,还需知道x的值,
这里x的取值对模型无影响,可取任意值(只对画出的图是否好看有影响)
xx = np.linspace(0,10)
print(xx)
[ 0. 0.20408163 0.40816327 0.6122449 0.81632653 1.02040816
1.2244898 1.42857143 1.63265306 1.83673469 2.04081633 2.24489796
2.44897959 2.65306122 2.85714286 3.06122449 3.26530612 3.46938776
3.67346939 3.87755102 4.08163265 4.28571429 4.48979592 4.69387755
4.89795918 5.10204082 5.30612245 5.51020408 5.71428571 5.91836735
6.12244898 6.32653061 6.53061224 6.73469388 6.93877551 7.14285714
7.34693878 7.55102041 7.75510204 7.95918367 8.16326531 8.36734694
8.57142857 8.7755102 8.97959184 9.18367347 9.3877551 9.59183673
9.79591837 10. ]
二维直线方程
w ∗ x + b = 0 ⟹ w 1 x 1 + w 2 x 2 + b = 0 ⟹ x 2 = − w 1 x 1 + b w 2 w*x+b = 0\implies w_1x_1 + w_2x_2 +b = 0\implies x_2 = -\frac{w_1x_1+b}{w_2} w∗x+b=0⟹w1x1+w2x2+b=0⟹x2=−w2w1x1+b
这里的 x 1 、 2 x_1、_2 x1、2为数据集不同维度上的数值;
下述 x x xx xx和 y y yy yy分别代表两个维度上的值。
yy = -(w[0] * xx + b) / w[1] # 根据一个维度的值可以计算出另一个维度的值
print(yy)
[-10.55592603 -10.12782781 -9.69972959 -9.27163137 -8.84353315
-8.41543493 -7.98733671 -7.55923849 -7.13114027 -6.70304206
-6.27494384 -5.84684562 -5.4187474 -4.99064918 -4.56255096
-4.13445274 -3.70635452 -3.2782563 -2.85015808 -2.42205986
-1.99396164 -1.56586342 -1.1377652 -0.70966699 -0.28156877
0.14652945 0.57462767 1.00272589 1.43082411 1.85892233
2.28702055 2.71511877 3.14321699 3.57131521 3.99941343
4.42751165 4.85560987 5.28370808 5.7118063 6.13990452
6.56800274 6.99610096 7.42419918 7.8522974 8.28039562
8.70849384 9.13659206 9.56469028 9.9927885 10.42088672]
通过支持向量绘制分割超平面
-
已知一点 ( x 0 , y 0 ) (x_0,y_0) (x0,y0)和斜率 a a a,求该直线方程: y − y 0 = a ( x − x 0 ) y-y_0=a(x-x_0) y−y0=a(x−x0)
-
已知直线的法向量为 n = ( m , b ) n=(m,b) n=(m,b),则直线的斜率为: a = − m b a = -\frac{m}{b} a=−bm
# 直线斜率
a = -w[0] / w[1]
# 选择第一个类别的支持向量,并计算y值
x_1 = clf.support_vectors_[0]
yy_dowm = a * (xx - x_1[0]) + x_1[1]
# 选择另一个类别的支持向量,并计算y值
x_2 = clf.support_vectors_[-1]
yy_up = a * (xx - x_2[0]) + x_2[1]
绘制模型示意图
将不同类别的数据放到一起。
其中:positie存放的是正类;negtive存放的是负类。
dataMat, labelMat = loadDataSet('G:\\desktop\\svmdata线性不可分 .txt')
def unique_index(L,f):
return [i for (i,v) in enumerate(L) if v==f]
pos = unique_index(labelMat, 1)
positive = []
for i in pos:
positive.append(dataMat[i])
positive = np.array(positive)
neg = unique_index(labelMat, -1)
negtive = []
for i in neg:
negtive.append(dataMat[i])
negtive = np.array(negtive)
# 绘制超平面及支持向量
plt.plot(xx, yy, 'r-')
plt.plot(xx, yy_dowm, 'k--')
plt.plot(xx, yy_up, 'k--')
# 将数据集上的点绘制到模型图中
plt.scatter(positive[:,0], positive[:,1], s=80, c='y')
plt.scatter(negtive[:,0], negtive[:,1], s=80, c='b')
# 绘制支持向量上的点
# plt.scatter(clf.support_vectors_[:,0], clf.support_vectors_[:,1], s=80, c='g')
plt.show()
效果展示
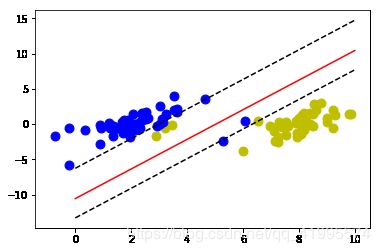
其中:黄色点为正类,蓝色点为负类。红线上方的黄色点和红线下方的蓝色点均为异常点。为了图像清晰,未画出支持向量。
总结: 由上述可以看出,线性可分和线性不可分sklearn实现svm的代码完全一样,所以,svm.SVC默认实现的是更复杂的线性不可分分类任务。
三、sklearn实现SVM非线性分类
import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm
%matplotlib inline
加载数据
此数据可以在我的github中获取。
def loadDataSet(fileName):
"""loadDataSet(对文件进行逐行解析,从而得到第行的类标签和整个数据矩阵)
Args:
fileName 文件名
Returns:
dataMat 数据矩阵
labelMat 类标签
"""
dataMat = []
labelMat = []
fr = open(fileName)
for line in fr.readlines():
lineArr = line.strip().split('\t')
dataMat.append([float(lineArr[0]), float(lineArr[1])])
labelMat.append(float(lineArr[2]))
return dataMat, labelMat
为样本和类别赋值
X,Y = loadDataSet('G:\\desktop\\svmdata非线性可分svm.txt')
X = np.array(X)
拟合数据
clf = svm.SVC(kernel='rbf',gamma='auto')
clf.fit(X,Y)
SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0,
decision_function_shape='ovr', degree=3, gamma='auto', kernel='rbf',
max_iter=-1, probability=False, random_state=None, shrinking=True,
tol=0.001, verbose=False)
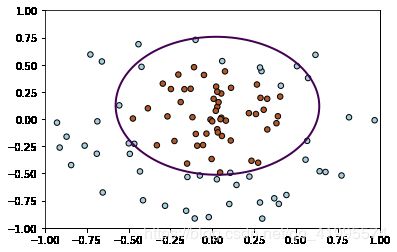
绘制模型图
xx,yy = np.meshgrid(np.linspace(-1,1,500),np.linspace(-1,1,500))
xy = np.vstack([xx.ravel(),yy.ravel()]).T
Z=clf.decision_function(xy).reshape(xx.shape)
# 绘制分类曲线
plt.contour(xx,yy,Z,levels=[0],linewidths=2)
# 画出数据集中各个类别的样本点
plt.scatter(X[:,0],X[:,1],s=30,c=Y,cmap=plt.cm.Paired, edgecolors='k')
plt.show()
进行预测
clf.predict([[1, 1]])
array([-1.])
clf.predict([[0, 0]])
array([1.])
【参考文献】
- apache github主页:https://github.com/apachecn/AiLearning
- sklearn SVM部分官网: https://scikit-learn.org/stable/modules/svm.html#svm-classification