二叉堆:优先队列的实现与堆排序
二叉堆的定义:
二叉堆(英语:binary heap)是一种特殊的堆,二叉堆是完全二叉树或者是近似完全二叉树。二叉堆满足堆特性:父节点的键值总是保持固定的序关系于任何一个子节点的键值,且每个节点的左子树和右子树都是一个二叉堆。
大根堆与小根堆的定义:
当父节点的键值总是大于左右孩子节点的键值时为最大堆。当父节点的键值总是小于左右孩子的键值时为最小堆。
二叉堆的应用:
优先队列、堆排序
二叉堆与二叉搜索树的区别:
二叉搜索树的每个节点值映射到一条直线上,必定是一个升序的有序数组;二叉堆(小根堆为例)则不一定,因为小根堆的根节点值只需要小于左右孩子节点就行,没有要求左右孩子节点值的大小顺序。
优先队列的实现:
可以基于无序数组、有序数组、无序链表、有序链表。在这里,我本人的代码是基于无序数组实现的,而优先队列是基于大根堆和无序数组实现的。
用二叉堆实现优先队列最关键也是最要的操作就是上浮(swim)和下沉(sink)
对于最大堆,会破坏堆性质的有有两种情况:
- 1)如果某个节点 A 比它的子节点(中的一个)小,那么 A 就不配做父节点,应该下去,下面那个更大的节点上来做父节点,这就是对 A 进行
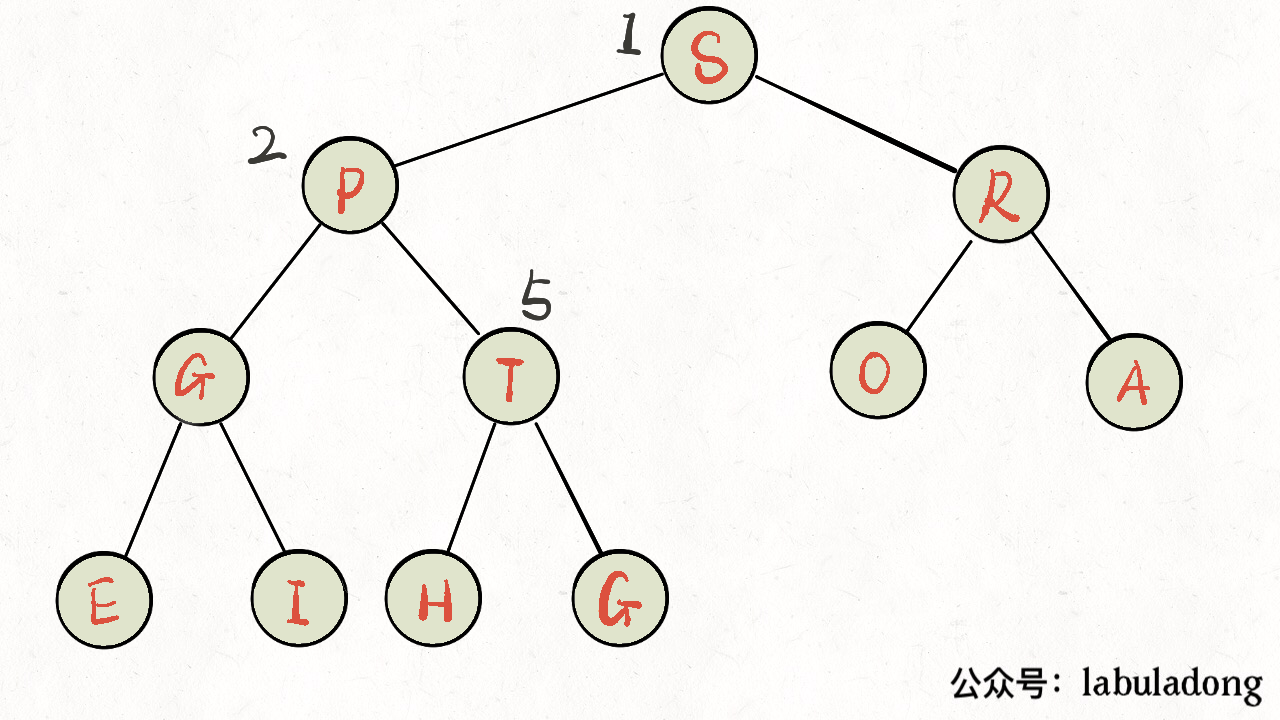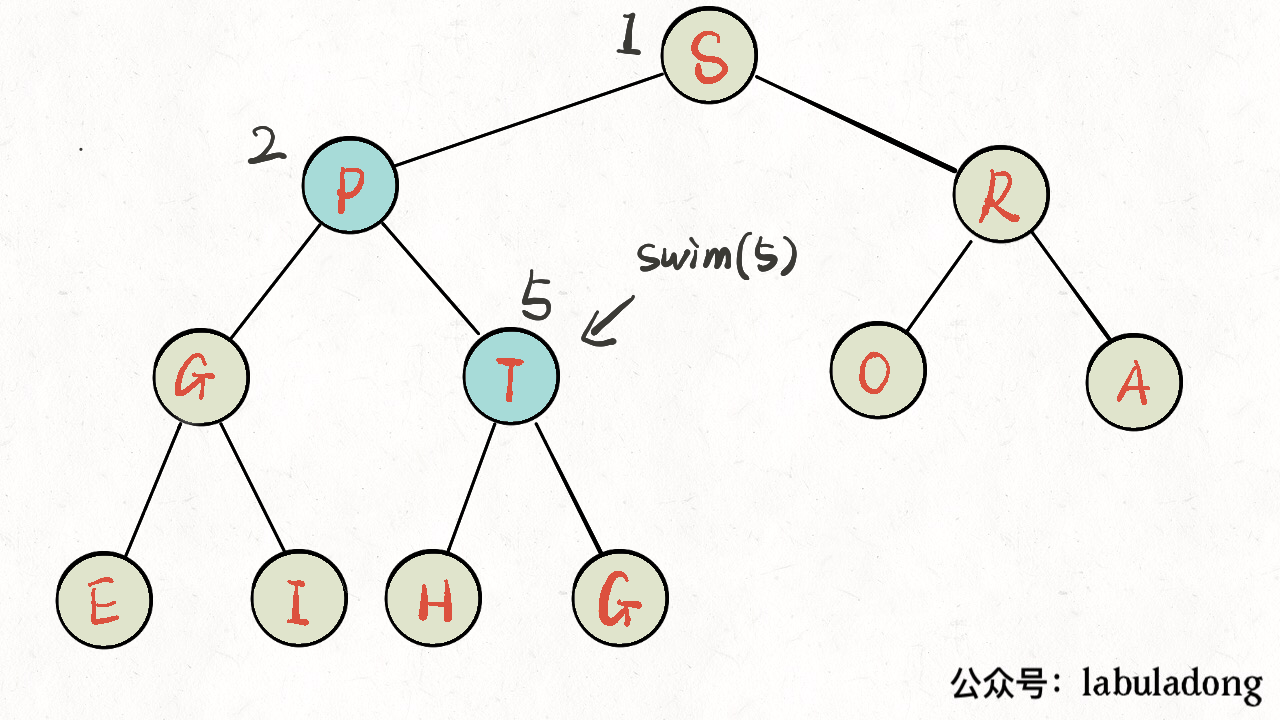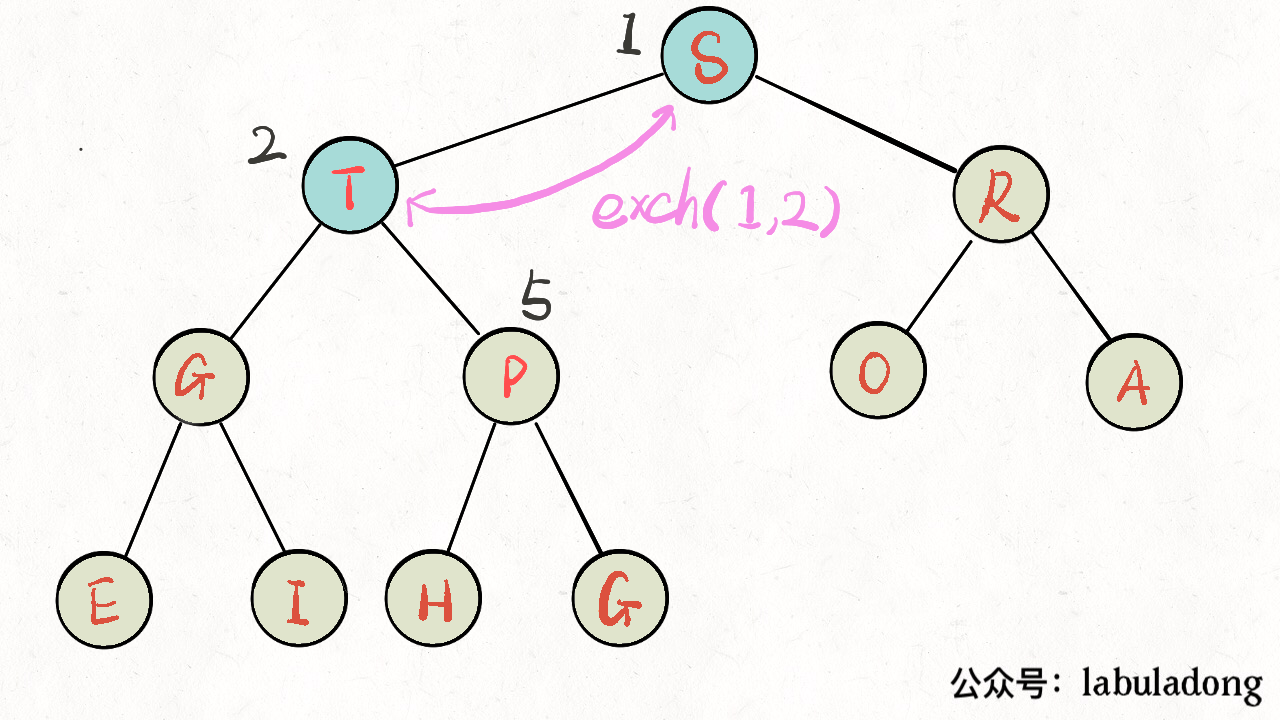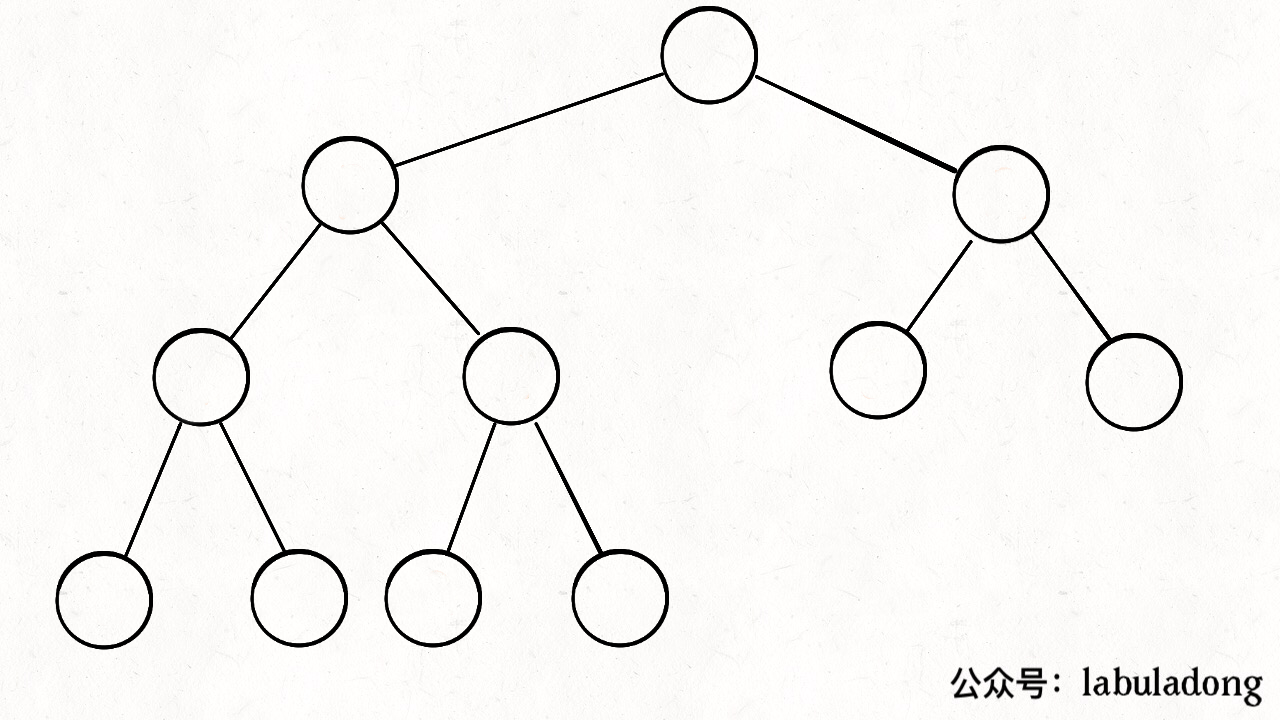
下沉。- 2)如果某个节点 A 比它的父节点大,那么 A 不应该做子节点,应该把父节点换下来,自己去做父节点,这就是对 A 的
上浮。
当然,错位的节点 A 可能要上浮(或下沉)很多次,才能到达正确的位置,恢复堆的性质。所以代码中肯定有一个 while 循环。
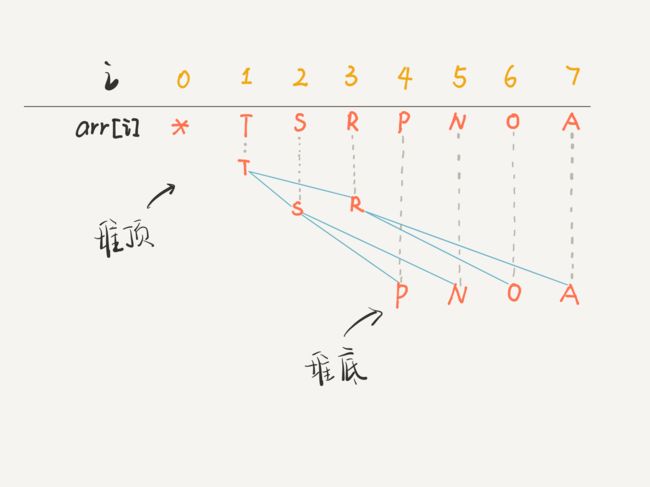
注:对于堆底元素我们使用的操作是上浮,对于堆顶元素我们使用的操作是下沉。
上浮代码实现:
template<typename T>
void Priority_Queue<T>::swim(int k) //由下至上堆有序化上浮
{
while (k > 0 && less(k / 2, k))
{
std::swap(vec[k / 2], vec[k]);
k = k / 2;
}
}
下沉代码实现:
template<typename T>
void Priority_Queue<T>::sink(int k) //由上至下堆有序化下沉
{
int size = vec.size();
while (2 * k <size)
{
int j = 2 * k;
//寻找子结点中的较大者
if (j < size && j + 1 < size && less(j, j + 1))j++;
//直到父节点大于子结点跳出循环
if (!less(k, j))break;
std::swap(vec[k], vec[j]);
k = j;
}
}
删除最大元素实现(等价于Priority_Queue.pop()):
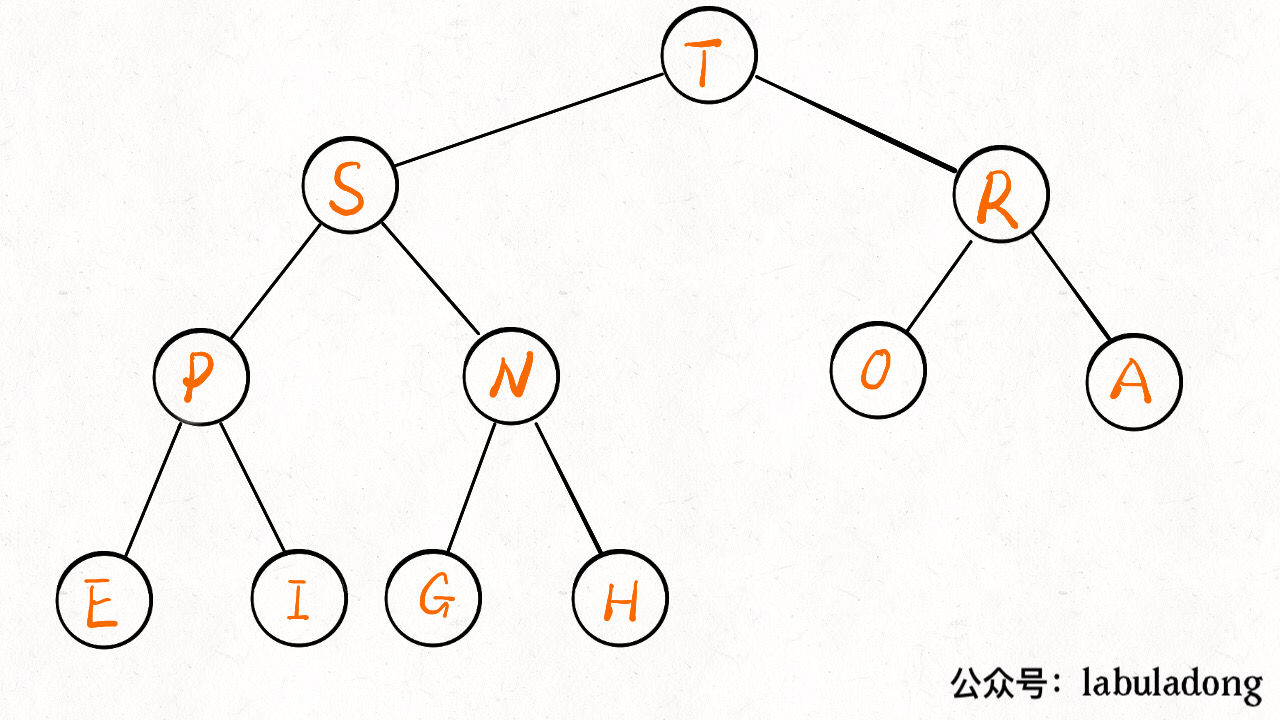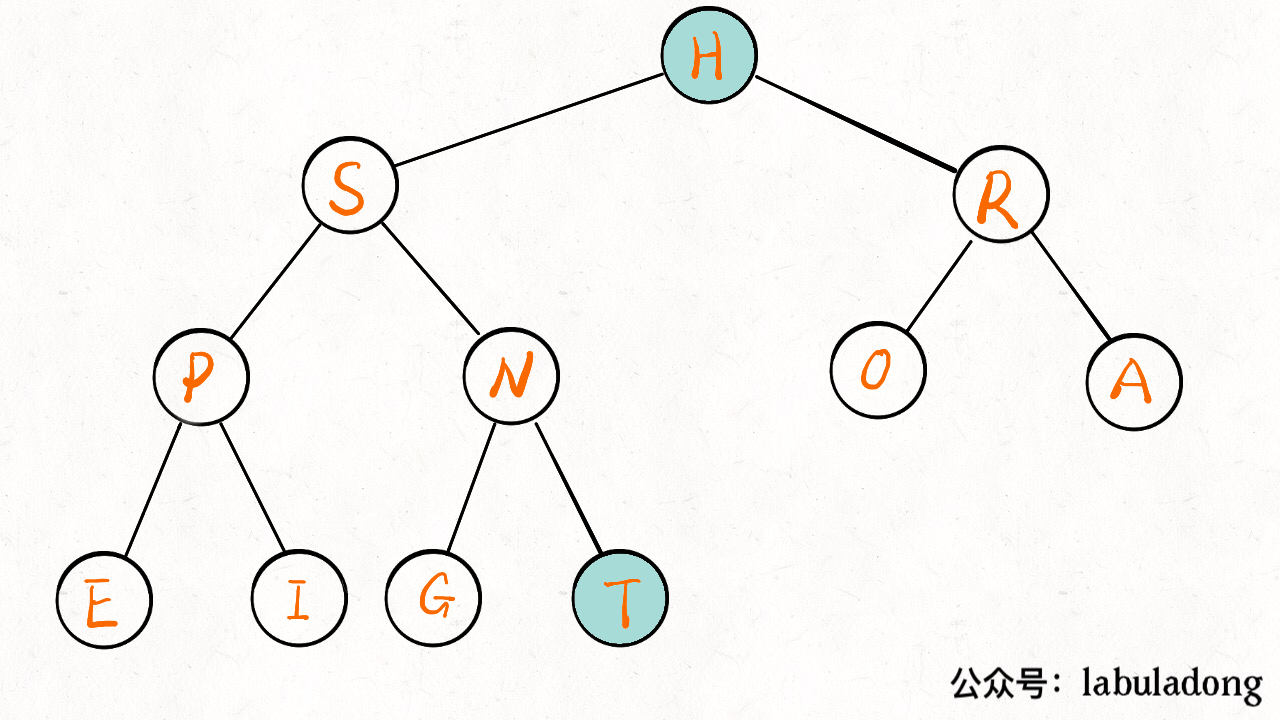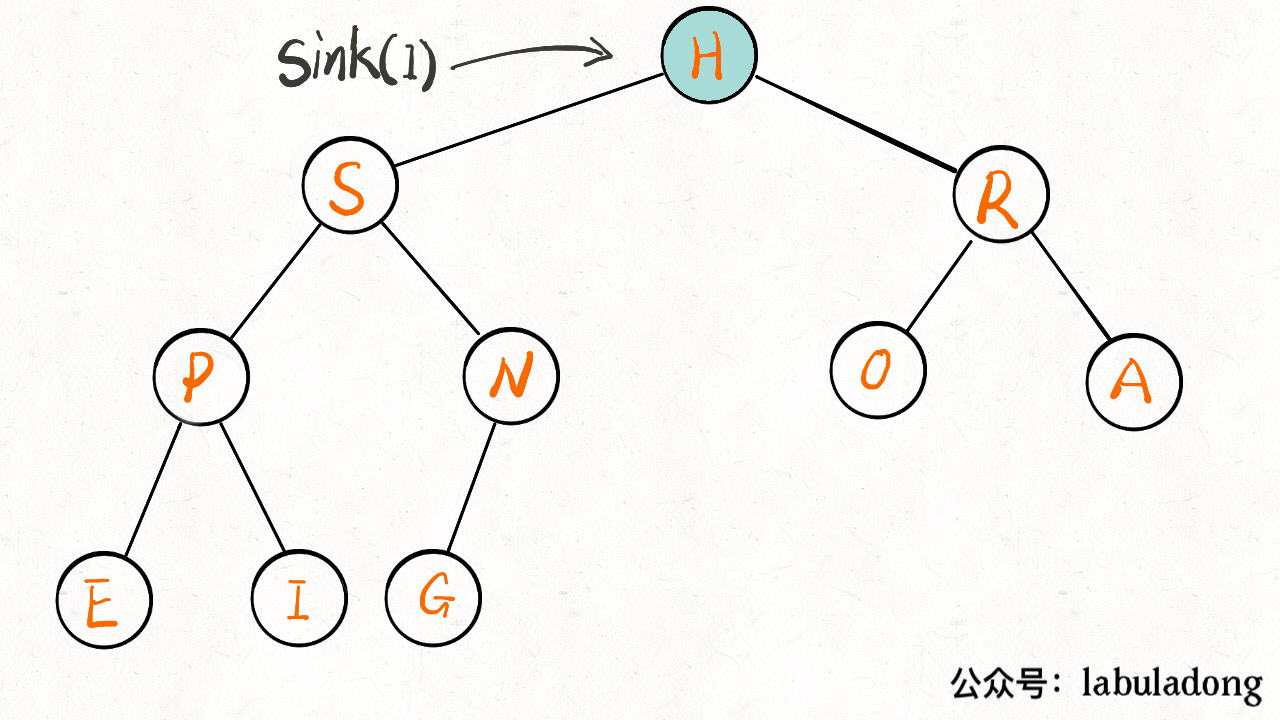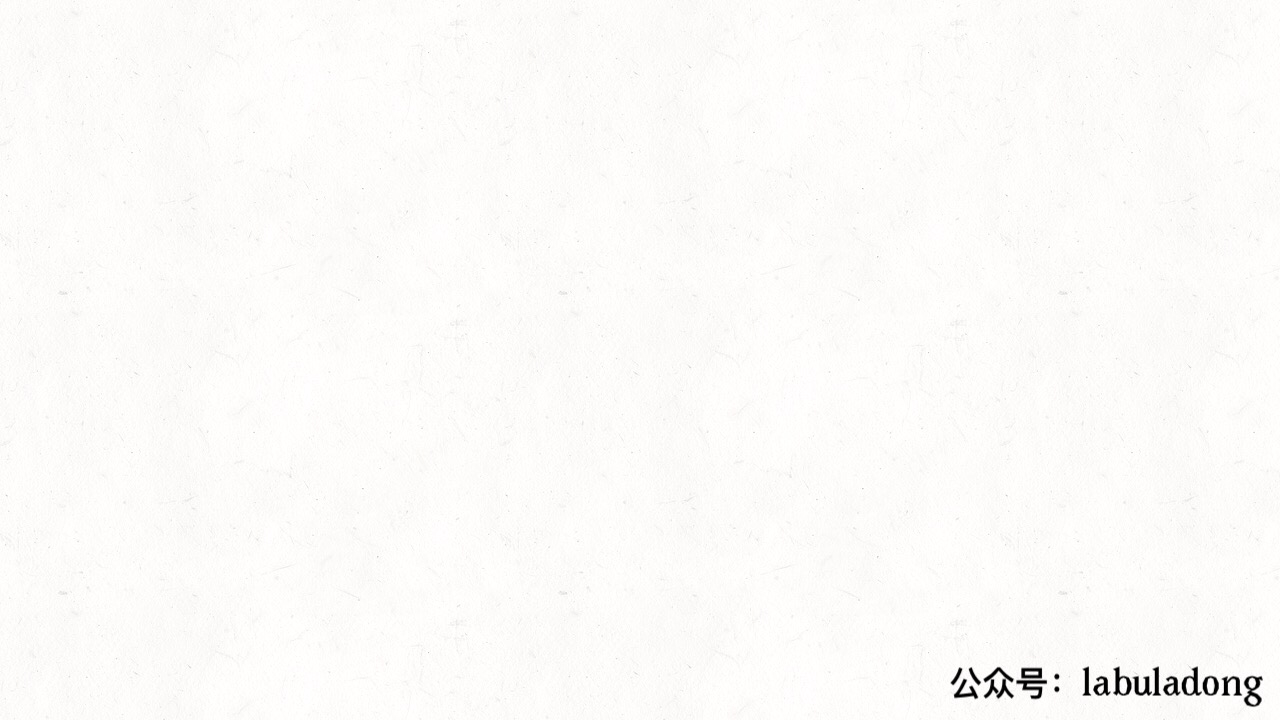
方法先把堆顶元素 A 和堆底最后的元素 B 对调,然后删除 A,最后让 B 下沉到正确位置。
template<typename T>
T Priority_Queue<T>::delMax()
{
T max = vec[0]; //从根结点获得最大元素
std::swap(vec[0],vec[vec.size()-1]); //将其和最后一个结点交换
vec.pop_back(); //删除根结点
sink(0); //第一个元素下沉恢复堆的有序性
return max;
}
插入元素实现(等价于Priority_Queue.push()):
方法先把要插入的元素添加到堆底的最后,然后让其上浮到正确位置。
template<typename T>
void Priority_Queue<T>::insert(const T& val)
{
vec.push_back(val);
swim(vec.size() - 1);//最后一个元素上浮
}
优先队列的实现的完整代码如下:
//Priority_Queue.h
#pragma once
#include 堆排序:
优先队列可以发展为一种排序方法,将所有元素插入一个查找最小元素的PQ,然后不断调用 delMin() 方法,即可得到有序数组。用无序数组实现的优先队列相当于进行一次插入排序。用堆实现的,则是堆排序。 堆排序中,直接调用swim()和 sink()方法,将需要排序的数组本身作为堆,不需要额外的存储空间。
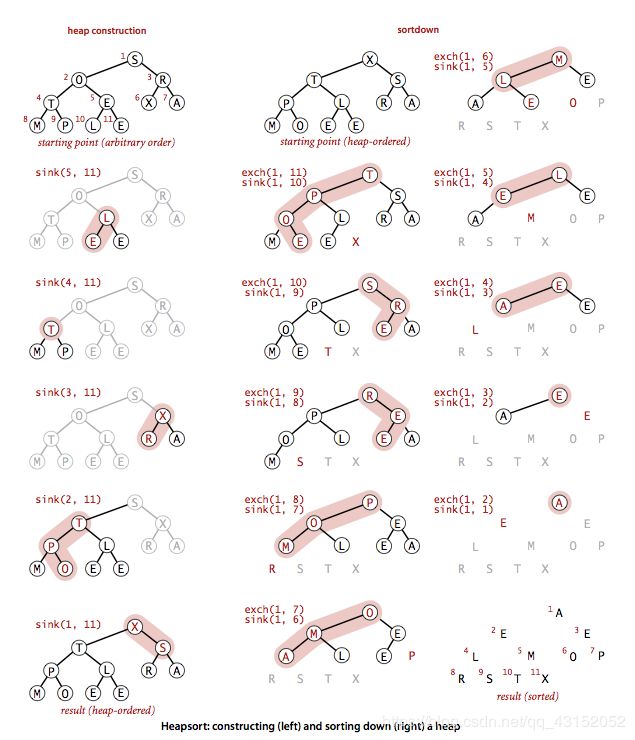
堆排序的两部分:
构造堆(将原始数组重新组织放入一个堆中)和下沉排序(按照降序取出原始构成排序结果)。
完整代码如下:
//sort_heap.h
bool less(std::vector<int>& vec, int i, int j)
{
return vec[i] < vec[j];
}
void sink(std::vector<int>& vec, int k, int N)
{
while (2 * k < N)
{
int j = 2 * k;
//寻找子结点中的较大者
if (j < N && j + 1 < N && less(vec, j, j + 1))j++;
//直到父节点大于子结点跳出循环
if (!less(vec, k, j))break;
std::swap(vec[k], vec[j]);
k = j;
}
}
void heap_sort(std::vector<int>& vec)
{
int size = vec.size() - 1;
for (int k = size / 2; k >= 0; k--)
sink(vec, k, size);
while (size > 1)//最后两个元素的顺序已经排好了,不需要交换
{
std::swap(vec[0], vec[size--]);//最大元素排在最后
sink(vec, 0, size);//首元素下沉
}
}
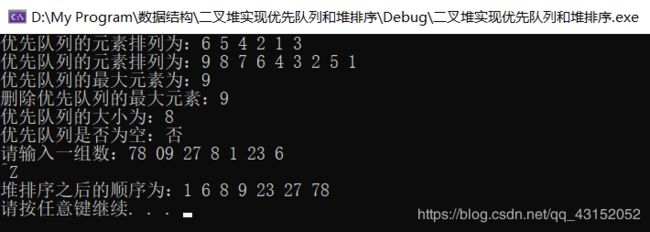
测试代码如下:
//test.cpp
#include "Priority_Queue.h"
#include "heap_sort.h"
#include