【深度学习】卷积层提速Factorized Convolutional Neural Networks
Wang, Min, Baoyuan Liu, and Hassan Foroosh. “Factorized Convolutional Neural Networks.” arXiv preprint arXiv:1608.04337 (2016).
本文着重对深度网络中的卷积层进行优化,独特之处有三:
- 可以直接训练。不需要先训练原始模型,再使用稀疏化、压缩比特数等方式进行压缩。
- 保持了卷积层原有输入输出,很容易替换已经设计好的网络。
- 实现简单,可以由经典卷积层组合得到。
使用该方法设计的分类网络,精度与GoogLeNet1, ResNet-182, VGG-163相当,模型大小仅2.8M。乘法次数 470×109 ,只有AlexNet4的65%。
标准卷积层
先来复习一下卷积的运算过程。标准卷积将3D卷积核(橙色)放置在输入数据 I (左侧)上,对位相乘得到输出 O (右侧)的一个像素(蓝色)。
卷积核在一个通道上的尺寸为 k2 ,输入、输出通道数分别为 m,n 。
当下流行的网络中,卷积层的主要作用是提取特征,往往会保持图像尺寸不变。缩小图像的步骤一般由pooling层实现。为书写简洁,这里认为输入输出的尺寸相同,都是 h×w 。
计算一个输出像素所需乘法次数为:
总体乘法次数为:
m,n 体现了对于特征的挖掘,取值较大,常为几百;相反, k 一般在1~5左右,很少超过7,高层次特征通过多个小尺寸卷积层实现。
优化的卷积层
本文介绍了三种卷积层的优化变种。
使用基层(bases)
设定核尺寸 k2 ,输入/输出通道数 m,n ,这个方法把卷积分成两个步骤。
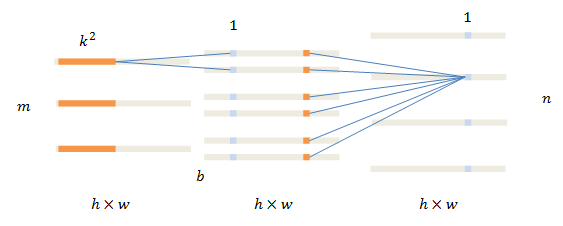
在第一个步骤中,输入的每一通道单独运算。在同样尺寸卷积核的作用下,每一通道计算得到 b 层结果。 m 通道数据变为 m×b 通道。中间结果的每一通道称为一个基层basis。
在第二个步骤中,各个通道进行合并,但使用的卷积核尺寸为1。
乘法数量为
与传统卷积所需的乘法次数比例为:
注意这里的大头是 n ,只要 b<k2 ,即可用较少的计算两实现较大核的卷积层。
提速示例
n k b rate 128 3 1 11.9% 128 3 5 59.5% 128 3 8 95.1% 128 5 8 38.3%
如果原有卷积核 k=1 ,这种方法无法提速。
重叠(stacked)的基层
对于输入输出通道数相同的情况( m=n ),可以进一步构造如下网络。
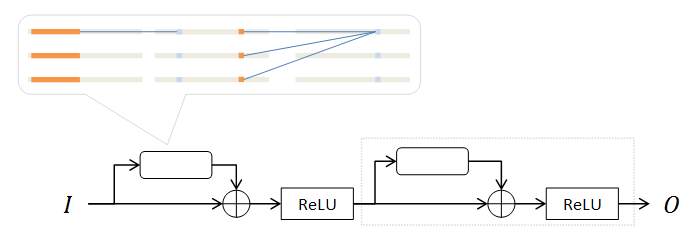
使用 b=1 的带基层的卷积层(圆角矩形),利用上述Residual方式,将运算重复 b 次。
对于相同的 b,n 取值,此网络乘法数量和前一个变种相同。但由于原来的并行计算改为串行(相当于增加深度),同时引入余量结构,此种网络的性能更佳。
拓扑连接
依然是 m=n 的情况,另一种优化思路是:减少输出通道和输入通道的连接数量。即,输出通道不再和所有输入通道有关,只和相邻的输入通道有关。
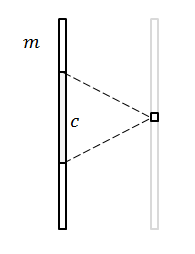
关于“相邻”,最直观的想法是,定义一个邻域大小 c ,每一个输出通道只和相邻的 c 个输入通道有关。
更巧妙的方法是,对输入通道数进行因式分解: m=∏i=1ndi
把原来的2+1维输入数据看做2+n维,在每一维定义一个邻域大小 ci 。对于输出的一个通道,只和其在n维空间中相邻的输入通道有关。

例子:30维分解为 d1=5,d2=6 ,第13个输出通道,在2维空间中坐标为 [3,3] 。邻域大小 c3=1,c2=1 。和该通道有关的范围为 [2,3,4;3] ,对应的输入通道为 [8,13,18] 。
这个变种同样适用于 k=1 的核。
实验
标准网络
选择ImageNet分类问题为实验对象。首先使用标准卷积层设计三个标准网络A,B,A’作为参照。基本结构如下:

白色为卷积,绿色为pooling。第一阶段是一个核较大的卷积,最后一阶段是average pooling,直接生成1000类分类结果。
中间四大阶段由max pooling和三个卷积层构成,其中后两个卷积层(粗线)输入/输出通道数相同,适于本文所述方法优化。
A网络的卷积核尺寸(问号处)为2,每两个卷积层添加一个Residual结构;B网络卷积核尺寸为3,每个卷积层添加一个Residual结构。
对于不太深的网络,Residual结构对精度提升不大,主要作用是加速训练过程。
A’网络和A相同,只是输入为164×164。
优化网络:基层
网络C,E由A演变而来,网络D,F由B演变来,其top-1精度以及计算复杂度如下:
| 网络 | 优化 | k | b | 精度 | 复杂度 |
|---|---|---|---|---|---|
| A | 无 | 2 | - | 59% | 1 |
| B | 无 | 3 | - | 62.1% | 2.25 |
| C | 基层 | 3 | 4 | 61.9% | ~1 |
| D | 基层 | 3 | 2 | 60.3% | ~0.5 |
| E | 重叠基层 | 3 | 2 | 63.1% | ~0.5 |
| F | 重叠基层 | 5 | 2 | 63.15% | ~0.5 |
使用重叠基层的卷积网络F,能够达到甚至超过原有网络B,计算复杂度不到原来25%。
优化网络:拓扑链接
将粗线所示卷积层的输入/输出通道进行分解,各层的因数 di ,邻域大小 ci ,top-1精度以及计算复杂度如下:
| 网络 | stage 1 | stage 2 | stage 3 | 精度 | 复杂度 |
|---|---|---|---|---|---|
| A’ | - | - | - | 54.2% | 1 |
| G | 8*16 - 4*8 | 16*16 - 8*8 | 16*32 - 8*16 | 53.6% | 0.5 |
| H | 4*8*4 - 2*5*3 | 8*8*4 - 4*5*3 | 8*8*8 - 4*5*6 | 52.9% | 0.47 |
达到相同性能,拓扑连接计算复杂度约为50%。
优化网络:复合
以A网络为基础,把两种优化方法组合,得到网络J,K:
| 网络 | 优化 | 精度 | 复杂度 |
|---|---|---|---|
| A | - | 59% | 1 |
| J | 卷积层加倍, 2D拓扑 | 58.9% | 0.5 |
| K | 卷积层加倍, 2D拓扑,层叠基准 | 60.1% | 0.25 |
只有25%计算复杂度,即超过原先网络。
优化网络:最终结果
综合前述实验结果,以网络E为基础,给出了ImageNet上分类问题的最佳网络L:

采用重叠的基层思想。每一个粗线白色模块的 b=1 ,两个不同输出通道数的模块为一组,重复6次。和A,E一样,每两个卷积层添加一个Residual结构。
- Christian Szegedy, Wei Liu, Yangqing Jia, Pierre Sermanet, Scott Reed, Dragomir Anguelov,
Dumitru Erhan, Vincent Vanhoucke, and Andrew Rabinovich. Going deeper with convolutions.
arXiv preprint arXiv:1409.4842, 2014. ↩ - Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. Deep residual learning for image
recognition. arXiv preprint arXiv:1512.03385, 2015. ↩ - K. Simonyan and A. Zisserman. Very deep convolutional networks for large-scale image
recognition. CoRR, abs/1409.1556, 2014. ↩ - Alex Krizhevsky, Ilya Sutskever, and Geoffrey E Hinton. Imagenet classification with deep
convolutional neural networks. In Advances in neural information processing systems, pages
1097–1105, 2012. ↩


