二进制+位操作 总结

扒了几篇博文，都是一些不符合需求的，对于一个数学渣渣来说，说的太简洁是会要命的，自己总结一下我碰到过的二进制。

参考资料：https://jingyan.baidu.com/article/1612d5008ff5b7e20f1eee4c.html

---

位运算（位运算符用来对二进制位进行操作）

  算术位运算：

   <1> 与：（and  / &）；< 2> 或：（or  /  | ）；  <3> 非：（ not  /  ~ ）  <4>  异或：( xor )

  移位运算：

   <1> 算术左移： <<

   <2> 算术右移： >>

  用法及实例：

     指定两个数 A = 60（0011 1100）; B = 13 （0000 1101）

1. 按位与（&）

   对两个数进行操作，然后返回一个新的数，这个数的每个位都需要两个输入数的同一位都为1时才为1，如下图：

   (A & B) 结果为 12, 二进制为 0000 1100

   

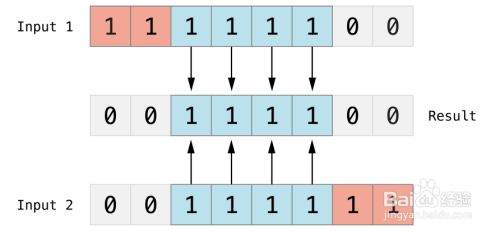
2. 按位或（|）

   比较两个数，然后返回一个新的数，这个数的每一位设置1的条件是两个输入数的同一位都不为0(即任意一个为1，或都为1)，如下图：

   (A | B) 结果为 61, 二进制为 0011 1101

   

3. 按位异或（^）

   比较两个数，然后返回一个数，这个数的每个位设为1的条件是两个输入数的同一位不同，如果相同就设为0，如下图：

   (A ^ B) 结果为 49, 二进制为 0011 0001

   

4. 按位取反（~）

   对一个操作数的每一位都取反，如下图：

   (~A ) 结果为 -61, 二进制为 1100 0011

   

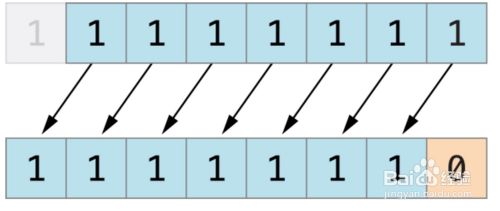
5. 按位左移（<<）

   将操作数的所有位向左移动指定的位数。

   下图展示了11111111 << 1（11111111 左移一位）的结果。蓝色数字表示被移动位，灰色表示被丢弃位，空位用橙色的0填充。

   （A << 2）结果为 240, 二进制为 1111 0000

   

6. 按位右移（<<）

   将操作数的所有位向又移动指定的位数。

   下图展示了11111111 >> 1（11111111 右移一位）的结果。蓝色数字表示被移动位，灰色表示被丢弃位，空位用橙色的0填充。

   A >> 2 结果为 15, 二进制为 0000 1111

   

---

带有二进制算法的程序

  1》求 m^n mod k =?

#include
using namespace std;
int m,n,k;
int main(){
    scanf("%d%d%d",&m,&n,&k);
    int ans=1;
    for(;n;n>>=1,m=(long long)m*m%k)
        if(n&1)
            ans=(long long) ans*m%k;
    printf("%d\n",ans);
    return 0;
}

  关于这个小程序的详解：https://blog.csdn.net/sodacoco/article/details/81587705

 

  2》辗转相除法的二进制算法

    1--原来的gcd算法代码

int GCD(int x,int y){
    return y==0?x:GCD(y,a%b);
}

    2--二进制改进后的gcd算法

    原理：（原理大部分都是对的，看不懂就再看，想不通就拿数字验证，强势理解它的存在，--来自一个数渣儿的蒟蒻经验）

   如果想进一步提高GCD的效率，可以通过不断去除因子2来降低常数，这就是所谓的“二进制算法”。

    具体实现：

      若x=y,则GCD(x,y)=x，否则：

      A，若 x,y 均为偶数 , 则GCD(x,y)=GCD(x/2 , y/2 ) ;

      B，若x为偶数，y为奇数 , 则GCD(x,y)=GCD(x/2 , y) ;

      C，若x为奇数，y为偶数 , 则GCD(x,y)=GCD(x , y/2) ;

      D，若 x,y 均为奇数 , 则GCD(x,y)=GCD(x-y, y) ;

#include
#include
using namespace std;
inline int GCD(int x,int y){
    int i,j;
    if(x==0)return y;
    if(y==0)return x;
    for(j=0;0==(x&1);++i) x>>=1;    //去掉所以的2
    for(j=0;0==(y&1);++j) y>>=1;    //去掉所有的2
    if(j>=1;       //去掉所有的2
    }
}

int main(){
    int x,y;
    while(1){
        cin>>x>>y;
        cout<

 

在原程序中插入一些cout，观察程序运行的具体方式（用乾隆的话说：盖满朕的大 cout 印 ）

（不懂的童鞋可以酱紫强势看懂程序，只不过有些麻烦）

#include
#include
using namespace std;
 
//递归输出二进制函数
void BinaryRecursion(int n)
{
    int a;
    a=n%2;
    n=n>>1;
    if (n==0);
    else
        BinaryRecursion(n);
    cout<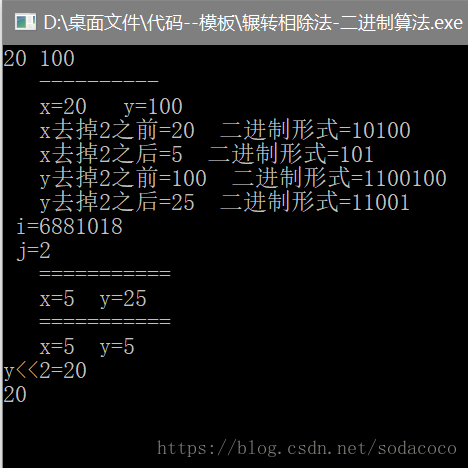
 
  
这样结合上述原理，不说完全理解，实现过程应该明白的差不多了。
 
  
 
  
  暂且整理这两个程序，对于二进制兴致大发是因为最近做的 组合数 的题目，大意是，求1-n中，与k互质的数，大意是将k分解质因子，然后从1-n中去除，用到了容斥定理，这些都能理解，自己也想明白了，就是搞不懂该怎么代码实现，看题解，看一个，二进制实现，看一个，二进制实现，硬着头皮去请教大佬二进制，结果还是没怎么明白，大佬默默的说了一句，下面的题好多都是二进制实现的，稍微看了一下，都说二进制能够实现好多不好实现的算法，再看看。