6.2 二叉树
在讨论一般树的存储结构及操作之前,我们首先分析下一种称为二叉树的抽象数据类型。
6.2.1、二叉树的定义
二叉树(Binary tree)是另一种特殊的树形结构,它的特点是每个树结点最多只能有两棵子树,并且二叉树的子树有左右之分,其次序不能任意颠倒。
抽象数据类型二叉树的定义如下:
ADT BinaryTree{
数据对象D:D是具有相同特性的数据元素的集合。
数据关系R:若D = Φ,则R = Φ,成Binary Tree为空二叉树。
若D ≠ Φ,则R = H,H是如下二元关系。省略
基本操作P:
InitBiTree(&T);
操作结果:构造空二叉树T。
DestroyBiTree(&T);
操作结果:销毁二叉树T。
CreateBiTree(&T,definition);
初始条件:definition给出二叉树T的定义。
操作结果:按definition构造二叉树T。
ClearBiTree(&T);
操作结果:将二叉树T清空。
BiTreeDepth(T);
操作结果:返回T的深度。
Root(T);
操作结果:返回T的根。
Value(T,e);
操作结果:返回e的值。
Assign(T,&e,value);
操作结果:结点e赋值value。
Parent(T,e);
操作结果:若e是T的非根结点,那么返回e的双亲,否则返回“空”。
LeftChild(T,e);
操作结果:返回e的左孩子,若e无左孩子,则返回“空”。
LeftSibling(T,e);
操作结果:返回e的左兄弟,若e是T的左孩子或e无左兄弟返回“空”。
省略……
}ADT BinaryTree
二叉树可以有5种基本形态。如下图
6.2.2、二叉树的性质
性质1、在二叉树的第i层至多有2的(i - 1)次方个结点。
性质2、深度为k的二叉树最多结点数为(2的k次方 - 1)个。
由性质1可知深度为k的二叉树的结点数为
性质3、对任何一个二叉树T,如果其终端结点数为n0,度为2的结点数为n2,则n0 = n2 + 1。
完全二叉树和满二叉树是两种特殊形态的二叉树。
一棵深度为k且有(2的k次方 - 1)个结点的二叉树称为满二叉树。如上图a所示那样的就是满二叉树。
如图b所示,一棵深度为4的完全二叉树。图b和c都是非完全二叉树。
可以对满二叉树的结点进行编号,约定编号从根结点开始,自上而下、从左到右
从深度为k的,有n个结点的二叉树,当且仅当其每一个结点都与深度为k的满二叉树中编号从1至n的结点一一对应时,称之为完全二叉树
完全二叉树将在很多场合下出现,下面介绍完全二叉树的两个重要性质。
性质4、具有n个结点的完全二叉树的深度为[log2 n] + 1
证明:假设深度为k,则根据性质2和完全二叉树的定义有
2^(k-1) -1 < n <= 2^k -1 或 2^(k-1) <= n < 2^k
于是(k - 1) <=[log2 n] < k,因为k是整数所以[log2 n] = k-1,即k = [log2 n] + 1
性质5、如果对一棵有n个结点的完全二叉树([log2 n] + 1)的结点按层次编号( 从第一层到第([log2 n] + 1) ),则对任一结点i(1<= i <=n),有
(1)如果i=1,那么结点i是二叉树的根,无双亲;如果i>1,则其双亲PARENT(i)是结点[i/2]。
(2)如果2i>n,则结点i无左孩子(结点i为叶子结点);否则其左孩子LCHILD(i)是结点2i。
(3)如果2i+1>n,则结点无右孩子,否则其右孩子RCHILD(i)是结点2i+1。
6.2.3 二叉树的顺序存储结构
1.顺序存储结构
//--------------------二叉树的顺序存储表示------------------------
#define MAX_TREE_SIZE 100 //二叉树的最大结点数
typedef TElemType SqBiTree[MAX_TREE_SIZE]; //0号单元存储根结点
SqBiTree bt;
按照顺序存储结构的定义,在此约定,用一组地址连续的存储单元来存储完全二叉树中自上而下、从左到右顺序排列的结点元素,即将完全二叉树的结点i元素存储在上面定义的一维数组的第(i-1)个下标分量里面。
图中0表示不存在此结点。由此可见,这种顺序存储结构只有完全二叉树合适.
2.链式存储结构
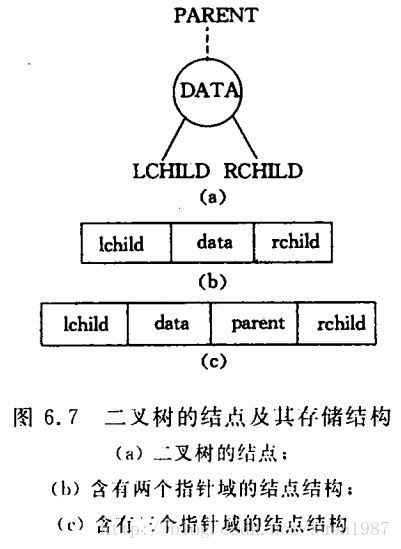
设计不同的结点结构可构成不同形式的链式存储结构。由二叉树的定义得知,二叉树的结点由一个数据元素和分别指向其左、右子树的两个分支构成,则表示二叉树的链表中的结点至少包含3个域:数据域和左右指针域,如下图b所示;有时为了方便找到双亲,则还在结点结构中增加了一个指向其双亲结点的指针域。
利用这两种结点结构所得二叉树的存储结构分别称为二叉链表和三叉链表,链表的头指针指向根结点。
//---------------------------------二叉树的二叉链表存储表示--------------------------------------
typedef struct BiTNode{
TElemType data;
struct BiTNode *lchild, *rchild;
}BiTNode, *BiTree;
Status CreateBiTree(BiTree &T)
{
//构造二叉链表表示的二叉树T
}
不同的存储结构中,实现实现二叉树的操作方法也不同,例如找双亲,在三叉链表中容易实现,而在二叉链表中比较麻烦点。由此,在具体应用中应该采用什么存储结构,除根据二叉树的形态外还应考虑进行何种操作。