ACM学习历程27——模式匹配

模式匹配是数据结构中字符串的一种基本运算，给定一个子串，要求在某个字符串中找出与该子串相同的所有子串，这就是模式匹配，通常模式匹配算法可以通过以下方式求解。
一、BF朴素模式匹配
该算法思想主要依靠循环遍历比较，设目标串为S，模式串为T，在外层循环中变量i指向目标串的某个位置，在内层循环中变量j=i，k=0。从k和j的位置开始，若S[j]与T[k]相等则j和k同时向后移动，若k能移动到模式串的结尾，则i为模式匹配的其实位置。反之，若在移动的过程中存在S[j]与S[k]不相等的地方，则结束内层循环，并将i向下移动一个单位，同时在内层循环中再次将i赋值给j，0赋值赋给k。BF算法的实现方式如下：

#include
#include
using namespace std;

void main()
{
    string s1,s2;
    int i=0,j=0,k=0;
    cout<<"s1:";
    cin>>s1;
    cout<<"s2:";
    cin>>s2;

    for(i=0;i0;
        while(j!=s1.length()&&k!=s2.length())
        {
            if(s1[j]==s2[k])
            {
                j++;
                k++;
            }
            else
                break;
        }
        if(k==s2.length())
        {
            cout<<"The start pos:"<break;
        }
    }
    if(i==s1.length())
        cout<<"Not match!"<123456789asd
s2:789a
The start pos:6

二、KMP模式匹配算法
KMP算法全称克努特—莫里斯—普拉特算法，该算法的关键是利用匹配失败后的信息，尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是实现一个next()函数，函数本身包含了模式串的局部匹配信息，时间复杂度O(m+n)。KMP算法需要考虑如下几种情形：
2.1 情形一

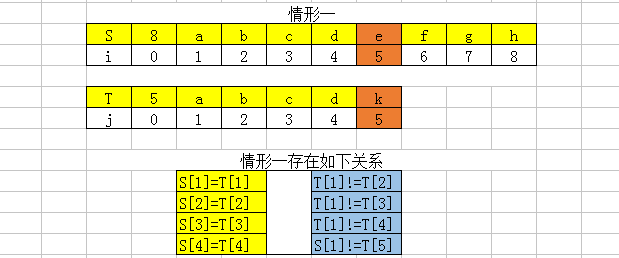
从上面的关系可知，由于T串中T[1]不与后面的任意一个字符相等且S[1]==T[1]，因此情形一匹配的部分属于唯一对应关系子串，但由于S[5]!=T[5]，所以对于T串来说，下一次开始的匹配位置为S[5]和T[1]。

2.2 情形二

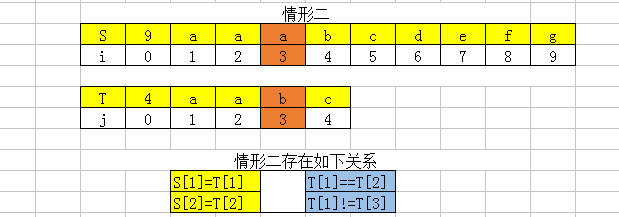
在情形二中存在匹配的部分S[1]==T[1]，S[2]==T[2]，但是在S[3]与T[3]的位置失配，考虑到T[1]==T[2]且T[1]!=T[3]，那么下一次开始配置的位置将不再是T[1]与S[2]，因为此种情况下由上述关系可知T[1]==S[2]的，所以开始匹配的位置为T[2]和S[3]。

2.3 情形三

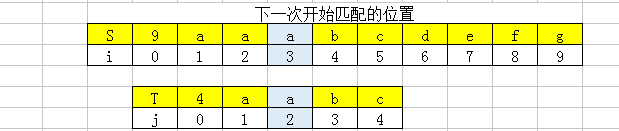
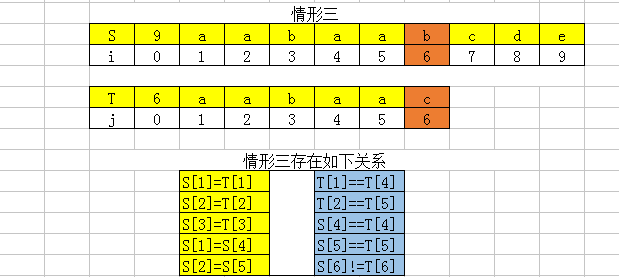
在情形三中，下标从0—5对应位置的S[i]和T[i]相等，但是在下标为6的位置出现了失配，从上面给出的等量关系中可知，在模式串中T[1]==T[4]，T[2]==T[5]且T[1]==S[4]，T[2]==S[5]，所以下一的判断匹配的位置可以从T[3]和S[6]的位置开始。

2.4 情形四

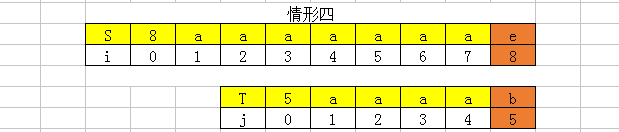
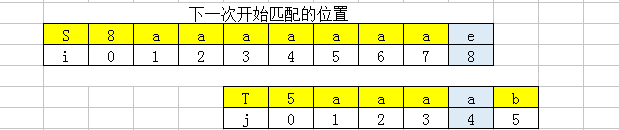
注：上述四种情况中，目标串和模式串的第一个位置存储的是串的长度。
2.5利用KMP算法需要求解next数组，通过这个数组可以在S[j]与S[k]不相等时，找到下一次回溯模式串回溯的下标。
2.5.1求解next数组

#include
#include
using namespace std;

void get_next(int *T,int *next)
{
    int i=0;
    int j=1;
    next[1]=0;
    int count=0;
    while(j0])
    {
        if(i==0 || T[i]==T[j])
        {
            i++;
            j++;
            next[j]=i;
        }
        else
        {   
            i=next[i];
        }
    }
}

void main()
{
    int T[30]={11,'a','b','c','a','b','c','a','b','b','a','c'};
    int next[25];
    get_next(T,next);
    for(int i=1;i<=11;i++)
        cout<" ";
    cout<0 1 1 1 2 3 4 5 6 1 2

2.5.2上述模式串是将字符的ASCII存储在数组数组中，数组的第一个位置存储模式串的长度，对于一个String类型的数据，由于第一个位置不是串的长度，因此需要对上面的代码进行适当的改动，代码如下：

#include
#include
using namespace std;

void get_next(string T,int next[])
{
    int i=-1;
    int j=0;
    next[0]=-1;
    while(jif(i==-1 || T[i]==T[j])
        {
            i++;
            j++;
            next[j]=i;
        }
        else
        {   
            i=next[i];
        }
    }
}

void main()
{
    string T="abcabcabbac";
    int next[30];
    get_next(T,next);
    for(int i=0;icout<" ";
    cout<1 0 0 0 1 2 3 4 5 0 1

2.5.3KMP算法

#include
#include
using namespace std;

void get_next(string T,int next[])
{
    int i=-1;
    int j=0;
    next[0]=-1;
    int count=0;
    while(jlength())
    {
        if(i==-1 || T[i]==T[j])
        {
            i++;
            j++;
            if(T[i]==T[j])
                next[j]=next[i];
            else
                next[j]=i;      
        }
        else
        {   
            i=next[i];
        }
    }
}

int Index_KMP(string s,string T,int pos)
{
    int i=pos;
    int j=1;
    int next[30];
    get_next(T,next);
    for(int k=0;klength();k++)
        cout<<next[k]<<" ";
    cout<while(i<s.length()&&jlength())
    {
        if(j==-1 || s[i]==T[j])
        {
            i++;
            j++;
        }
        else
            j=next[j];
    }
    return (j==T.length())?i-T.length():-1;
}

void main()
{
    string s="abcabcaabcabcabbacb";
    string T="abcabcabbac";

    cout<<s<int pos=Index_KMP(s,T,0);
    cout<<pos<1 0 0 -1 0 0 -1 0 5 -1 1
7