【实时渲染】一篇文章让你学会做一个软件光栅化渲染器

如果您想更好的理解本文所讲内容，建议您阅读scratchapixel及《3D游戏与计算机图形学中的数学方法》第五章和第七章。

通过本文，您将会实现一个简单的软件光栅化渲染器，并会进一步理解渲染流水线所做的事。本文会通过一个简单的样例介绍以下知识：

1.纹理
2.深度缓冲
3.坐标变换
4.基础光照（漫反射光照，镜面光照，环境光照）。
5.透视校正插值（深度插值，顶点属性插值）

样例效果：

1.样例源码GitHub地址。

2.所需图片地址。

首先是自定义的一些数据

	vec2 uv0 = { 0,0 };
	vec2 uv1 = { 0,1 };
	vec2 uv2 = { 1,1 };
	vec2 uv3 = { 1,0 };
	vec2 uv4 = { 1,1 };

	vec3 v0 = { -48,  -48, 0 };
	vec3 v1 = { -48, 48,  0 };
	vec3 v2 = { 48, 48,  0 };
	vec3 v3 = { 48,  -48, 0 };
	vec3 v4 = { 48, -48, 96 };

	vec3 lightpos = { 0,0,100 };
	vec3 viewpos = { 0,0,0 };
	vec3 lightcolor = { 1,1,1 };

	unsigned const int nx = 512, ny = 512;

1.三维数学库
三维数学库总的源码在这里，主要包含三角形结构体（tra），二维、三维、四维向量类，点乘、叉乘、反射、旋转、平移、单位化函数，大部分是比较容易理解的，注意一下向量乘法运算符的重载、反射和旋转。

2判断像素是否在三角形内

float edgeFun(const vec3 &a, const vec3 &b, const vec3 &c)
{
	return (c[0] - a[0]) * (b[1] - a[1]) - (c[1] - a[1]) * (b[0] - a[0]);
}

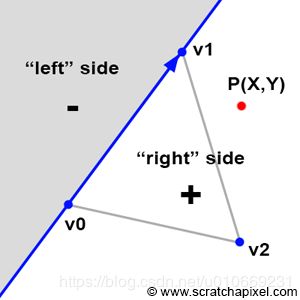
这里采用的是Linear Expression Evaluation方法，简单的说，就是将v0,v1，p的x，y坐标带入下面的这个函数,根据结果判断p点位置：

1.E（p）>0:p在v0 v1的“右”侧
2.E（p）<0:p在v0 v1的“左”侧
3.E（p）=0:p在v0 v1的边上

此处v0，v1，v2是以顺时针方向排列的，如果以逆时针方向的话则判断方式相反。

其实就是（p-v0）和（v1-v0）向量的叉乘：

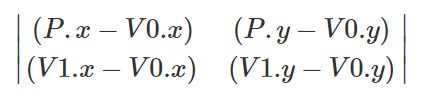
2.通过面积比求顶点属性插值

所以这个函数返回值的模是以（p-v0）和（v1-v0）为邻边的平行四边形的面积，即以v0，v1，v2为顶点的三角形面积的两倍。
对于给定的一个像素位置p（x，y，0），如果其返回值均大于等于零则其位于该三角形内。若已判定p在三角形内，则根据面积比求出w，用于下一步的顶点属性插值。

透视投影、屏幕映射、深度插值、顶点属性插值

tra trangle(vec3 v0, vec3 v1, vec3 v2,vec2 uv0,vec2 uv1,vec2 uv2, int nx, int ny)
{
	float d = 1;//投影平面到原点距离
	//透视投影
	v0[0] = (v0[0] * d) / v0[2];
	v0[1] = (v0[1] * d) / v0[2];

	v1[0] = (v1[0] * d) / v1[2];
	v1[1] = (v1[1] * d) / v1[2];

	v2[0] = (v2[0] * d) / v2[2];
	v2[1] = (v2[1] * d) / v2[2];
	//屏幕映射
	v0[0] = (1 + v0[0])*0.5*nx;	v0[1] = (1 + v0[1])*0.5*ny;
	v1[0] = (1 + v1[0])*0.5*nx;	v1[1] = (1 + v1[1])*0.5*ny;
	v2[0] = (1 + v2[0])*0.5*nx;	v2[1] = (1 + v2[1])*0.5*ny;
	//
	v0[2] = 1 /v0[2]; v1[2] = 1 / v1[2]; v2[2] = 1 / v2[2];
	
	return tra(v0, v1, v2, uv0, uv1, uv2);
}

3.透视投影

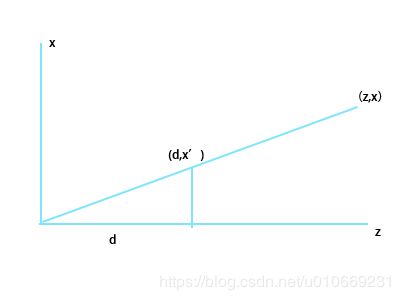
以x-z坐标为例，如图将点（x,0,z）投影到距观察点（原点）为d的屏幕上
x/x’=z/d 即x=z*(x’/d)。

4.屏幕映射
即x’=（nx+x*nx）/2，其中nx为屏幕宽度。
x=-1时映射到0。
x=0时映射到（nx）/2。
x=1是映射到nx。

5.深度插值&&顶点属性插值
公式推导在这里及其下一章，本文不再详细介绍，总之最后得到两个结论：
1.三角形面上z值的倒数是线性插值。

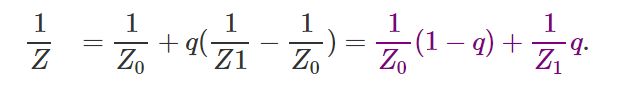
2.三角形面上的插值属性与z坐标值倒数的乘积（c/z）是线性插值。

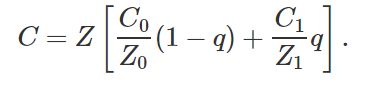
光栅化时，图形处理器首先计算1/z的线性插值，在计算其倒数，最后乘以b/z的线性插值结果，则可获得顶点属性b的透视校正插值结果。
对应代码：

Trangle函数：
v0[2] = 1 /v0[2]; v1[2] = 1 / v1[2]; v2[2] = 1 / v2[2];

Color函数：
float xxx = w0 * tr.uv0[0]* tr.v0.z + w1 * tr.uv1[0] * tr.v1.z + w2 * tr.uv2[0] * tr.v2.z;
float yyy = w0 * tr.uv0[1] * tr.v0.z + w1 * tr.uv1[1] * tr.v1.z + w2 * tr.uv2[1] * tr.v2.z;

z = 1 / (w0*tr.v0[2] + w1 * tr.v1[2] + w2 * tr.v2[2]);

xxx *= z; yyy *= z;

其中tr.uv[0]是uv值，通过插值得到p点的uv值（xxx，yyy）。
6.纹理采样

载入贴图，所需头文件在stbi_image.h里，长和宽的数据存储在w和h里。

unsigned char *data = stbi_load("container.jpg", &w, &h, &nchannel, 0);

纹理采样 这里的xxx，yyy是uv值

r = ((int)data[3 * int(xxx*w) + 3 * int(yyy*h)*w]) / 255.0;
g = ((int)data[3 * int(xxx*w) + 3 * int(yyy*h)*w+1])/255.0;
b = ((int)data[3 * int(xxx*w) + 3 * int(yyy*h)*w+2])/255.0;

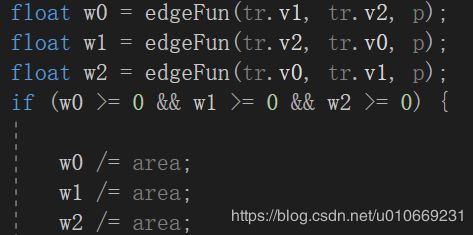
获得P点像素颜色的代码

vec4 Color(vec3 &p, tra &tr, float area,unsigned char *data)
{
	
	float r = 0, g = 0, b = 0, z = 0, zz = 0;
	float w0 = edgeFun(tr.v1, tr.v2, p);	
	float w1 = edgeFun(tr.v2, tr.v0, p);
	float w2 = edgeFun(tr.v0, tr.v1, p);
	if (w0 >= 0 && w1 >= 0 && w2 >= 0) {

		w0 /= area;
		w1 /= area;
		w2 /= area;

		float xxx = w0 * tr.uv0[0]* tr.v0.z + w1 * tr.uv1[0] * tr.v1.z + w2 * tr.uv2[0] * tr.v2.z;
		float yyy = w0 * tr.uv0[1] * tr.v0.z + w1 * tr.uv1[1] * tr.v1.z + w2 * tr.uv2[1] * tr.v2.z;

		z = 1 / (w0*tr.v0[2] + w1 * tr.v1[2] + w2 * tr.v2[2]);

		xxx *= z; yyy *= z;

		r = ((int)data[3 * int(xxx*w) + 3 * int(yyy*h)*w]) / 255.0;
		g = ((int)data[3 * int(xxx*w) + 3 * int(yyy*h)*w+1])/255.0;
		b = ((int)data[3 * int(xxx*w) + 3 * int(yyy*h)*w+2])/255.0;
	}
	else
	{		
		r = 0; g = 0; b = 0;
	}
	return vec4(r, g, b, z);
}

7.深度测试
首先生成一个深度缓冲

float zBuffer[nx][ny] ;

然后遍历所有三角形（这个例子只有三个），如果位于该三角形像素的z值小于zbuffer存储的Z值，则更新像素的rgb值及zbuffer的值。

			if (pix1.w < zBuffer[i][j] && pix1.w)
			{
				rr = pix1.x;
				gg = pix1.y;
				bb = pix1.z;
				zBuffer[i][j] = pix1.w;
			}
			if (pix2.w < zBuffer[i][j] && pix2.w)
			{
				rr = pix2.x;
				gg = pix2.y;
				bb = pix2.z;
				zBuffer[i][j] = pix2.w;
			}
			if (pix3.w < zBuffer[i][j] && pix3.w)
			{
				rr = pix3.x;
				gg = pix3.y;
				bb = pix3.z;
				zBuffer[i][j] = pix3.w;
			}

8.基础光照
《3D数学》这本书中的思路是对顶点法向量N，指向光源的方向L和观察者方向V进行插值，计算每个像素的光照公式。
但是在LearnOpenGL中好像是先在顶点着色器中存储p点位于世界空间的FragPos，再在片段着色其中进行光照计算，本文是模拟第二种方式进行计算的，思路就是由某点像素坐标值p（x，y，0）逆推出p在世界空间中的坐标值在进行光照计算。

	v0[0] = (1 + v0[0])*0.5*nx;	v0[1] = (1 + v0[1])*0.5*ny;
	v1[0] = (1 + v1[0])*0.5*nx;	v1[1] = (1 + v1[1])*0.5*ny;
	v2[0] = (1 + v2[0])*0.5*nx;	v2[1] = (1 + v2[1])*0.5*ny;

	v0[2] = 1 /v0[2]; v1[2] = 1 / v1[2]; v2[2] = 1 / v2[2];

通过上述代码我们可以逆推出P点在世界空间中的坐标：

zz = pix1.w;
xx = ((2 * p.x) / nx - 1)*zz;
yy = ((2 * p.y) / ny - 1)*zz;

之后进行光照计算，光照模型参考这里

if (zBuffer[i][j] == FLT_MAX)
{
		zBuffer[i][j] = 1;
}
else
{
	z = zBuffer[i][j];

	vec3 fragpos = vec3(xx, yy, zz);
	vec3 lightdir = lightpos - fragpos;
	vec3 viewdir = viewpos - fragpos;

	normal = normalize(normal);				
	lightdir = normalize(lightdir);				
	viewdir = normalize(viewdir);

	float diff = max(dot(lightdir, normal), 0);

	vec3 rec = reflect(lightdir, normal);
	rec = normalize(rec);

	float spec = pow(max(dot(rec, viewdir), 0), 16);

	vec3 result = lightcolor * (0.1 + spec + diff);

	vec3 col = result * vec3(rr, gg, bb);

	rr = col.x;
	gg = col.y;
	bb = col.z;
}

令所得RGB值不大于1

rr = rr > 1 ? 1 : rr;
gg = gg > 1 ? 1 : gg;
bb = bb > 1 ? 1 : bb;

最后输出到ppm文件里

outfile << " " << int(rr*255.99) << " " << int(gg*255.99) << " " << int(bb*255.99);

感谢您的阅读，祝您生活愉快~~