数据结构(C语言)第二版 第八章课后答案
数据结构(C语言)第二版 第八章课后答案
1.选择题
1~5 C D B D C
6~10 B C D B C
11~15 B C C D A
(1)从未排序序列中依次取出元素与已排序序列(初始时为空)中的元素进行比较,将其放入已排序序列的正确位置上的方法,这种排序方法称为(C) 。
A.归并排序 B.冒泡排序
C.插入排序 D.选择排序
(2)从未排序序列中挑选元素,并将其依次放入已排序序列(初始时为空)末端的方法,称为(D) 。
A.归并排序 B.冒泡排序 C.插入排序 D.选择排序
(3)对n 个不同的关键字由小到大进行冒泡排序,在下列(B)情况下比较的次数最多。
A.从小到大排列好的 B .从大到小排列好的
C.元素无序 D .元素基本有序
对关键字进行冒泡排序,关键字逆序时比较次数最多。
(4)对 n 个不同的排序码进行冒泡排序,在元素无序的情况下比较的次数最多为(D) 。
A. n+1 B. n C. n-1 D. n(n-1)/2
比较次数最多时,第一次比较n-1 次,第二次比较n-2 次, 最后一次比较1次,即(n-1)+(n-2)+ … +1= n(n-1)/2 。
(5)快速排序在下列(C)情况下最易发挥其长处。
A.被排序的数据中含有多个相同排序码
B.被排序的数据已基本有序
C.被排序的数据完全无序
D.被排序的数据中的最大值和最小值相差悬殊
B 选项是快速排序的最坏情况。
(6)对n 个关键字作快速排序,在最坏情况下,算法的时间复杂度是(B) 。
A. O(n) B . O(n2) C. O(nlog 2n) D . O(n3)
快速排序的平均时间复杂度为O(nlog 2n) ,但在最坏情况下,即关键字基本排好序的情况下,时间复杂度为O(n2)。
(7)若一组记录的排序码为( 46,79,56,38,40,84),则利用快速排序的方法,以第一个记录为基准得到的一次划分结果为(C) 。
A.38,40,46,56,79,84
B.40,38,46,79,56,84
C.40,38,46,56,79,84
D.40,38,46,84,56,79
(8)下列关键字序列中,(D)是堆。
A.16,72, 31, 23, 94,53
B.94,23, 31, 72, 16,53
C.16,53, 23, 94, 31,72
D.16,23, 53, 31, 94,72
(9)堆是一种(B)排序。
A.插入 B.选择 C.交换 D.归并
(10 )堆的形状是一棵(C) 。
A.二叉排序树B.满二叉树C.完全二叉树D .平衡二叉树
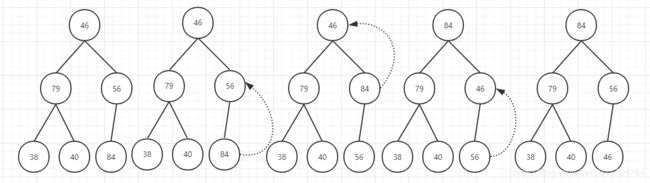
(11)若一组记录的排序码为( 46, 79, 56 , 38, 40, 84 ),则利用堆排序的方法建立的初始堆为(B) 。
A.79,46,56,38,40,84
B.84,79,56,38,40,46
C.84,79,56,46,40,38
D.84,56,79,40,46,38
(12)下述几种排序方法中,要求内存最大的是(C) 。
A.希尔排序B.快速排序C.归并排序D.堆排序
堆排序、希尔排序的空间复杂度为O(1) ,快速排序的空间复杂度为O(log 2n),归并排序的空间复杂度为O(n) 。
(13)下述几种排序方法中, (C)是稳定的排序方法。
A.希尔排序B .快速排序C.归并排序D.堆排序
不稳定排序有希尔排序、简单选择排序、快速排序、堆排序;
稳定排序有直接插入排序、折半插入排序、冒泡排序、归并排序、基数排序。
(14)数据表中有10000 个元素,如果仅要求求出其中最大的10 个元素,则采用(D)算法最节省时间。
A.冒泡排序B .快速排序C.简单选择排序D.堆排序
局部排序 选择堆排序
(15)下列排序算法中,(A)不能保证每趟排序至少能将一个元素放到其最终的位置上。
A.希尔排序B .快速排序C.冒泡排序D.堆排序
快速排序的每趟排序能将作为枢轴的元素放到最终位置;
冒泡排序的每趟排序能将最大或最小的元素放到最终位置;
堆排序的每趟排序能将最大或最小的元素放到最终位置。
2.应用题
(1)设待排序的关键字序列为 {12 , 2, 16 , 30 , 28, 10, 16* , 20 , 6, 18} ,试分别写出使用以下排序方法,每趟排序结束后关键字序列的状态。
①直接插入排序
②折半插入排序
③希尔排序(增量选取5, 3, 1 )
④冒泡排序
⑤快速排序
⑥简单选择排序
⑦堆排序
⑧二路归并排序
直接插入排序:
{12 , 2, 16 , 30 , 28, 10, 16* , 20 , 6, 18}
[2 12] 16 30 28 10 16* 20 6 18
[2 12 16] 30 28 10 16* 20 6 18
[2 12 16 30] 28 10 16* 20 6 18
[2 12 16 28 30] 10 16* 20 6 18
[2 10 12 16 28 30] 16* 20 6 18
[2 10 12 16 16* 28 30] 20 6 18
[2 10 12 16 16* 20 28 30] 6 18
[2 6 10 12 16 16* 20 28 30] 18
[2 6 10 12 16 16* 18 20 28 30]
②折半插入排序排序过程同①
[2 12] 16 30 28 10 16* 20 6 18
[2 12 16] 30 28 10 16* 20 6 18
[2 12 16 30] 28 10 16* 20 6 18
[2 12 16 28 30] 10 16* 20 6 18
[2 10 12 16 28 30] 16* 20 6 18
[2 10 12 16 16* 28 30] 20 6 18
[2 10 12 16 16* 20 28 30] 6 18
[2 6 10 12 16 16* 20 28 30] 18
[2 6 10 12 16 16* 18 20 28 30]
③希尔排序(增量选取5, 3, 1)
④冒泡排序
2 12 16 28 10 16* 20 6 18 [30]
2 12 16 10 16* 20 6 18 [28 30]
2 12 10 16 16* 6 18 [20 28 30]
2 10 12 16 6 16* [18 20 28 30]
2 10 12 6 16 [16* 18 20 28 30]
2 10 6 12 [16 16* 18 20 28 30]
2 6 10 [12 16 16* 18 20 28 30]
2 6 10 12 16 16* 18 20 28 30]
⑤快速排序
12[6 2 10] 12 [28 30 16* 20 16 18]
6[2] 6 [10] 12 [28 3016* 20 16 18 ]
28 2 6 10 12 [18 16 16* 20 ] 28[30 ]
182 6 10 12 [16* 16] 18 [20] 28 30
16* 2 6 10 12 16* [16] 18 20 28 30
左子序列递归深度为1 ,右子序列递归深度为3
⑥简单选择排序
2 [12 16 30 28 10 16* 20 6 18]
2 6 [16 30 28 10 16* 20 12 18]
2 6 10 [30 28 16 16* 20 12 18]
2 6 10 12 [28 16 16* 20 30 18]
2 6 10 12 16 [28 16* 20 30 18]
2 6 10 12 16 16* [28 20 30 18]
2 6 10 12 16 16* 18 [20 30 28]
2 6 10 12 16 16* 18 20 [28 30]
2 6 10 12 16 16* 18 20 28 [30]
⑧二路归并排序
2 1216 30102816 * 206 18
2 12 16 3010 16* 2028 6 18
2 10 12 16 16* 20 28 306 18
2 6 10 12 16 16* 18 20 28 30
(2)给出如下关键字序列{ 321 , 156 , 57 , 46 , 28 , 7, 331 , 33, 34 , 63},试按链式基数排序方法,列出每一趟分配和收集的过程。
(3)对输入文件( 101 , 51 , 19, 61 , 3, 71 , 31, 17, 19 , 100, 55 , 20, 9, 30 , 50 ,6, 90 );当k=6 时,使用置换- 选择算法,写出建立的初始败者树及生成的初始归并段。
3.算法设计题
(1)试以单链表为存储结构,实现简单选择排序算法。
[ 算法描述]
void LinkedListSelectSort(LinkedList head){
p=head->next;
while( p!=null){
q=p->next; r=p; // 设r 是指向关键字最小的结点的指针
while (q!=null){
if(q->data<r->data) r=q;
q:=q->next;
}
if(r!= p) r->data<-->p->data;
p=p->next;
}
}
(2)有n 个记录存储在带头结点的双向链表中, 现用双向冒泡排序法对其按上升序进行排序,请写出这种排序的算法。(注:双向冒泡排序即相邻两趟排序向相反方向冒泡)
typedef struct node{
ElemType data;
struct node *prior,*next;
}node , *DLinkedList;
void TwoWayBubbleSort(DLinkedList la){ // 对存储在带头结点的双向链表la 中的元素进行双向起泡排序。
int exchange=1;
DLinkedList p,temp,tail;
head=la;
tail=null;
while (exchange){
p=head->next;
exchange=0;
while (p->next!=tail) {
if (p->data>p->next->data){
temp=p->next; exchange=1;
p->next=temp->next;temp->next->prior=p;
temp->next=p; p->prior->next=temp;
temp->prior=p->prior; p->prior=temp;
}
else p=p->next; // 无交换,指针后移
tail=p; // 准备向上起泡
p=tail->prior;
while (exchange && p->prior!=head){ // 向上(左)起泡,一趟有一最小元素冒出
if (p->data<p->prior->data){ // 交换两结点指针,涉及6 条链
temp=p->prior; exchange=1; // 有交换
p->prior=temp->prior;temp->prior->next=p ; // 先将temp 结点从链表上摘下
temp->prior=p; p->next->prior=temp; // 将temp 插到p 结点后(右)
temp->next=p->next; p->next=temp;
}
else p=p->prior;
}
} // 无交换,指针前移
head=p; // 准备向下起泡
}
}
(3)设有顺序放置的n 个桶,每个桶中装有一粒砾石,每粒砾石的颜色是红,白,蓝之一。要求重新安排这些砾石,使得所有红色砾石在前,所有白色砾石居中,所有蓝色砾石居后,重新安排时对每粒砾石的颜色只能看一次,并且只允许交换操作来调整砾石的位置。
void QkSort(rectype r[],int n) {
int i=1,j=1,k=n,temp;
while (k!=j){
while (r[k].key==3) k--; // 当前元素是兰色砾石,指针左移
if (r[k].key==1){ // 当前元素是红色砾石
if (i>=j){temp=r[k];r[k]=r[i];r[i]=temp; i++;} // 左侧只有红色砾石,交换r[k] 和r[i]
else {
temp=r[j];r[j]=r[i];r[i]=temp; j++; // 左侧已有红色和白色砾石,先交换白色砾石到位
temp=r[k];r[k]=r[i];r[i]=temp; i++; // 白色砾石( i 所指)和待定砾石( j 所指)
}
}
if (r[k].key==2){
if (i<=j) { temp=r[k];r[k]=r[j];r[j]=temp; j++;} // 左侧已有白色砾石,交换r[k] 和r[j]
else { temp=r[k];r[k]=r[i];r[i]=temp; j=i+1;} //i 、j 分别指向红、白色砾石的后一位置
}
}
if (r[k]==2) j++; //处理最后一粒砾石
else if (r[k]==1) { temp=r[j];r[j]=r[i];r[i]=temp; i++; j++; }
}
(4)编写算法,对n 个关键字取整数值的记录序列进行整理,以使所有关键字为负值的记录排在关键字为非负值的记录之前,要求:
①采用顺序存储结构,至多使用一个记录的辅助存储空间;
②算法的时间复杂度为O(n) 。
void process (int A[n]){
low = 0;
high = n-1;
while ( low<high ){
while (low<high && A[low]<0) low++;
while (low<high && A[high]>0) high++;
if (low<high){
x=A[low];
A[low]=A[high];
A[high]=x;
low++; high--;
}
}
return;
}
(5)借助于快速排序的算法思想, 在一组无序的记录中查找给定关键字值等于key 的记录。设此组记录存放于数组r[l…n] 中。若查找成功,则输出该记录在r 数组中的位置及其值,否则显示“ not find ”信息。请简要说明算法思想并编写算法。
int index (RecType R[],int l,h,datatype key){
int i=l,j=h;
while (i<j){
while (i<=j && R[j].key>key) j--;
if (R[j].key==key) return j;
while (i<=j && R[i].key<key) i++;
if (R[i].key==key) return i;
}
cout<<"Not find " ;
return 0;
}
(6)有一种简单的排序算法,叫做计数排序。这种排序算法对一个待排序的表进行排序,并将排序结果存放到另一个新的表中。必须注意的是,表中所有待排序的关键字互不相同,计数排序算法针对表中的每个记录,扫描待排序的表一趟,统计表中有多少个记录的关键字比该记录的关键字小。假设针对某一个记录,统计出的计数值为c,那么,这个记录在新的有序表中的合适的存放位置即为c 。
①给出适用于计数排序的顺序表定义;
②编写实现计数排序的算法;
③对于有n 个记录的表,关键字比较次数是多少?
④与简单选择排序相比较,这种方法是否更好?为什么?
typedef struct{
int key;
datatype info
}RecType
// 计数排序算法,将a 中记录排序放入b 中
void CountSort(RecType a[],b[],int n){
for(i=0;i<n;i++){ // 对每一个元素
for(j=0,cnt=0;j<n;j++)
if(a[j].key<a[i].key) cnt++; // 统计关键字比它小的元素个数
b[cnt]=a[i];
}
}
//③ 对于有n 个记录的表,关键码比较 n^2次。
//④ 简单选择排序算法比本算法好。简单选择排序比较次数是n(n-1)/2, 且只用一个交换记录的空间;而这种方法比较次数是n^2,且需要另一数组空间。
for(i=0;i<n;i++) a[i].count=0;// 各元素再增加一个计数域,初始化为0
for(i=0;i<n;i++)
for(j=i+1;j<n;j++)
if(a[i].key<a[j].key) a[j].count++; else a[i].count++;