分治 —— 莫队算法 —— 普通莫队
【思想基础】
普通莫队常用于维护区间答案，比如：对于一个长度为 n 的序列，给出 m 次询问，每次询问区间 [l,r] 内有多少个不同的颜色，其中 n,m<=100000.
首先考虑暴力，对于每次询问，遍历一遍 [l,r]，这样的时间复杂度是 O(n*m) 的，最坏时间复杂度肯定会超时，那么考虑换一种方式进行暴力。
定义 ql、qr，表示区间 [ql,qr] 内有多少种颜色，再定义 cnt 数组，cnt[i] 表示第 i 种颜色在区间 [ql,qr] 中出现的次数，然后一个个处理询问，对于询问 [l,r]，挪动 ql 到 l，qr 到 r.
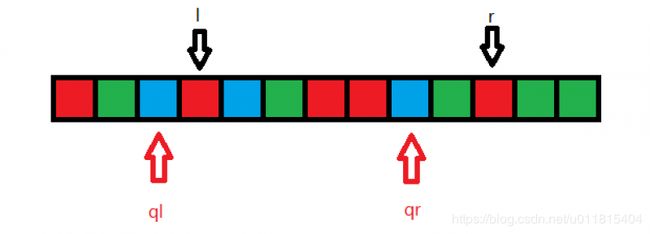
以下图为例，进行模拟：
对于区间 [ql,qr]，初始状态如上，假设蓝色为 1，红色为 2，绿色为 3，那么：cnt_1=3，cnt_2=3，cnt_3=1
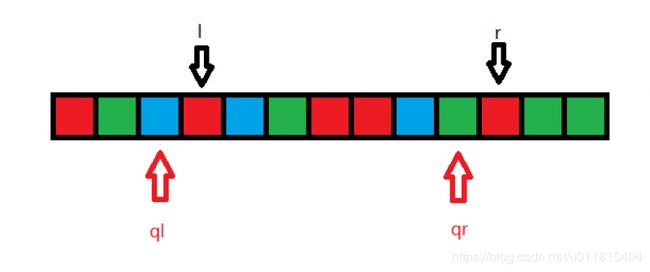
将 qr 向右挪一下，那么多了一个绿色，使得：cnt_3=cnt_3+1=2
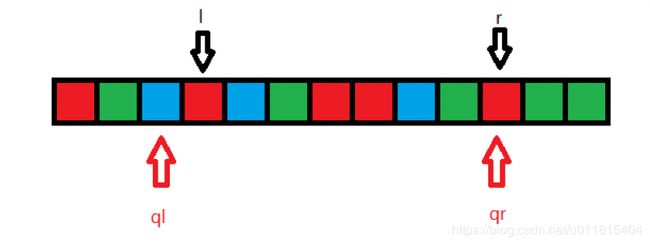
将 qr 继续向右挪动，那么多了一个红色，使得：cnt_2=cnt_2+1=4，此时可以发现，右指针 qr 与询问右端点 r 重合，那么可以对左指针进行挪动
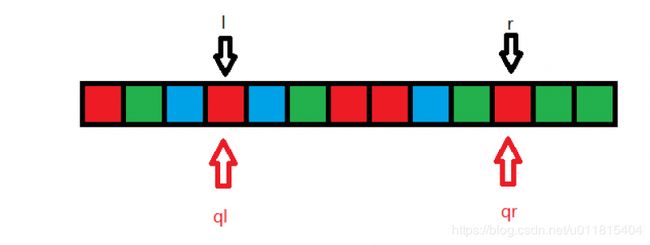
对 ql 向右挪动，那么少了一个蓝色，使得：cnt_1=cnt_1-1=2，此时左指针 ql 与询问左端点 l 重合，可得出答案：cnt_1=2，cnt_2=4，cnt_3=2.
通过以上模拟可以发现，每次挪动都是 O(1)，每次询问最多挪动 n 次，这样时间复杂度依旧是 O(n*m)，但通过对以上过程的模拟可以发现，这样暴力的耗时就消耗在挪动次数上，因此只要让挪动的次数尽可能的少就可以极大的降低时间复杂度。
而要想让挪动次数尽可能的小，可以将 m 次询问全部存储下来，然后按照某种方法进行排序，从而减少挪动次数，但这样的方法是强行离线，然后进行排序，因此普通莫队是不支持修改的。
int l=1,r=0,ans=0;
for(int i=1;i<=m;i++){
while(l>q[i].l) add(--l);//[l-1,r]
while(lq[i].r) del(r--);//[l,r-1]
res[q[i].id]=ans;//存储答案
} 【分块】
对于 n 与 m 同阶的情况，一般设块长度为 
，经过排序后，每个块内均摊有 个询问的 l 左端点，那么显然这 l 个端点的右端点是有序的，最多会移动 n 次，因此对于每个块的时间复杂度是 O(n)，然后有 个块，那么这样的总复杂度为 
，而对于询问 m 特别大的情况， 会超时，因此需要用到其他的长度。
设块长度为 S，那么对于任意多个在同一块内的询问，挪动的距离就是 n，一共有 
个块，移动的总次数就是 
，由于移动时可能会跨块，因此还需要加上一个 O(m*S) 的复杂度，故而总复杂度为 
，由于我们需要让这个值尽可能的小，通过简单的数学运算可以得出，S 取 
是最优的，此时时间复杂度为 
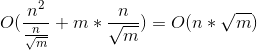，而在随机情况下，块的大小为 
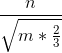是最优的，大约是原来的 0.9 倍。
需要注意的是，分块时块的大小不是固定的，要根据题目具体分析，分析的过程如上面分析 m 极大时的复杂度。
block=n/sqrt(m*2/3*1.0);//分块，不卡常数时
block=sqrt(m*2/3*1.0);//分块，卡常数时【排序】
将 m 次询问强制离线进行进行排序，一种方法是优先按照左端点进行排序，这样的排序可以保证左端点只会右挪，但右端点最坏的情况还是每次从最前面挪动到最后面，再从最后面挪到最前面，这样的时间复杂度依然是 O(n*m)，因此要考虑一种使左右端点挪动次数尽可能少的排序方法。
考虑将长度为 n 的序列分为 个长度为 的块，若左端点在同一个块内，则按照右端点排序，即以左端点所在块为第一关键字，右端点位置为第二关键字。
bool cmp(node a,node b){//正常排序
if(a.l/block==b.l/block)//左端点在一个块中
return a.r正常排序时，由于每个块的右端点都是按照从小到大排序的，当指针跳回左边后处理下一个块又要跳回右边，增加了不必要的移动，因此，此时可以按照奇偶性排序进行优化：当左端点的块为奇数时，右端点按照从小到大排；当左端点的块偶数时，右端点按照从大到小排。这样可以保证指针移到右边不用再跳回左边，减少一半的操作，理论上可以快一倍。
bool cmp(Node a,Node b){//按照奇偶性排序
if( (a.l/block)==(b.l/block) ){//当左端点位于同一个块时
if( (a.l/block)%2 )//左端点的块序号为奇数时
return a.rb.r;//按照从大到小排
}
else//当左端点不位于同一个块时
return a.lb.r );
} 【模版】
1.统计 [l,r] 中相同的数的个数
struct Node{
int l,r;//询问的左右端点
int id;//询问的编号
}q[N];
int n,m,a[N];
int block;//分块
int ans,cnt[N];//cnt[i]为i在当前区间出现次数
int res[N];
bool cmp(Node a,Node b){//奇偶性排序
return (a.l/block)^(b.l/block)?a.lb.r);
}
void add(int x){//统计新的
if(!cnt[a[x]])
ans++;
cnt[a[x]]++;
}
void del(int x){//减去旧的
cnt[a[x]]--;
if(!cnt[a[x]])
ans--;
}
int main(){
//序列
scanf("%d",&n);
for(int i=1;i<=n;++i)
scanf("%d",&a[i]);
//询问
scanf("%d",&m);
for(int i=1;i<=m;i++){
scanf("%d%d",&q[i].l,&q[i].r);
q[i].id=i;
}
block=n/sqrt(m*2/3*1.0);//分块，不卡常数时
//block=sqrt(m*2/3*1.0);//分块，卡常数时
sort(q+1,q+m+1,cmp);//对询问进行排序
int l=1,r=0;//左右指针
for(int i=1;i<=m;i++){
int ql=q[i].l,qr=q[i].r;//询问的左右端点
while(l>ql) add(--l);//[l-1,r]
while(lqr) del(r--);//[l,r-1]
res[q[i].id]=ans;//获取答案
}
for(int i=1;i<=m;i++)
printf("%d\n",res[i]);
return 0;
} 2. 统计 [l,r] 中有出现次数与其值相同的数的个数
struct Node{
int l,r;//询问的左右端点
int id;//询问的编号
}q[N];
int n,m,a[N];
int block;//分块
LL ans,cnt[N];//cnt[i]为i在当前区间出现次数
LL res[N];
bool cmp(Node a,Node b){//奇偶性排序
return (a.l/block)^(b.l/block)?a.lb.r);
}
void add(int x){//统计新的
if(cnt[a[x]]==a[x])
ans--;
cnt[a[x]]++;
if(cnt[a[x]]==a[x])
ans++;
}
void del(int x){//减去旧的
if(cnt[a[x]]==a[x])
ans--;
cnt[a[x]]--;
if(cnt[a[x]]==a[x])
ans++;
}
int main(){
while(scanf("%d%d",&n,&m)!=EOF){
for(int i=1;i<=n;++i){
scanf("%d",&a[i]);
if(a[i]>n)//大于n肯定不符合
a[i]=-1;
}
for(int i=1;i<=m;i++){
scanf("%d%d",&q[i].l,&q[i].r);
q[i].id=i;
}
ans=0;
memset(cnt,0,sizeof(cnt));
block=sqrt(m*2/3*1.0);//分块，卡常数
sort(q+1,q+m+1,cmp);//对询问进行排序
int l=1,r=0;//左右指针
for(int i=1;i<=m;i++){
int ql=q[i].l,qr=q[i].r;//询问的左右端点
while(l>ql) add(--l);//[l-1,r]
while(lqr) del(r--);//[l,r-1]
res[q[i].id]=ans;//获取答案
}
for(int i=1;i<=m;i++)
printf("%lld\n",res[i]);
}
return 0;
}