写了一个简单的贝叶斯分类器

贝叶斯的复杂程度因样本特征而决定，因先验函数决定，因似然函数模型决定。
今天写了一个简单的贝叶斯分类器，两种特征，两类标签。
数据用的李航老师《统计学习方法》的例4.1

截图1

截图2

截图3

源代码如下：

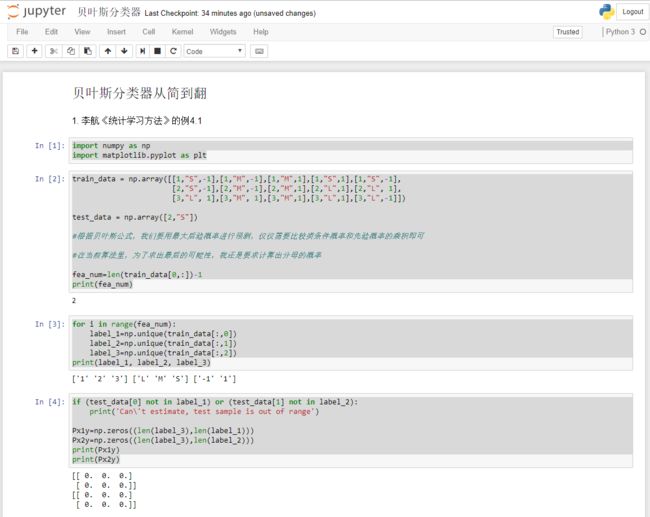
import numpy as np
import matplotlib.pyplot as plt
train_data = np.array([[1,"S",-1],[1,"M",-1],[1,"M",1],[1,"S",1],[1,"S",-1],
                       [2,"S",-1],[2,"M",-1],[2,"M",1],[2,"L",1],[2,"L", 1],
                       [3,"L", 1],[3,"M", 1],[3,"M",1],[3,"L",1],[3,"L",-1]])

test_data = np.array([2,"S"])

#根据贝叶斯公式，我们要用最大后验概率进行预测，仅仅需要比较类条件概率和先验概率的乘积即可

#在当前算法里，为了求出最后的可能性，我还是要求计算出分母的概率

fea_num=len(train_data[0,:])-1
print(fea_num)
for i in range(fea_num):
    label_1=np.unique(train_data[:,0])
    label_2=np.unique(train_data[:,1])
    label_3=np.unique(train_data[:,2])
print(label_1, label_2, label_3)
if (test_data[0] not in label_1) or (test_data[1] not in label_2):
    print('Can\'t estimate, test sample is out of range')

Px1y=np.zeros((len(label_3),len(label_1)))
Px2y=np.zeros((len(label_3),len(label_2)))
print(Px1y)
print(Px2y)
for i in np.arange(len(label_3)):
    for j in np.arange(len(label_1)):
        inx=(train_data[:,0]==label_1[j]) & (train_data[:,2]==label_3[i])
        inx1=train_data[:,2]==label_3[i]
        num1=len(train_data[inx1,:])
        num=len(train_data[inx,:])
        Px1y[i,j]=num/num1
    for k in np.arange(len(label_2)):
        inx=(train_data[:,1]==label_2[k]) & (train_data[:,2]==label_3[i])
        num=len(train_data[inx,:])
        Px2y[i,k]=num/num1
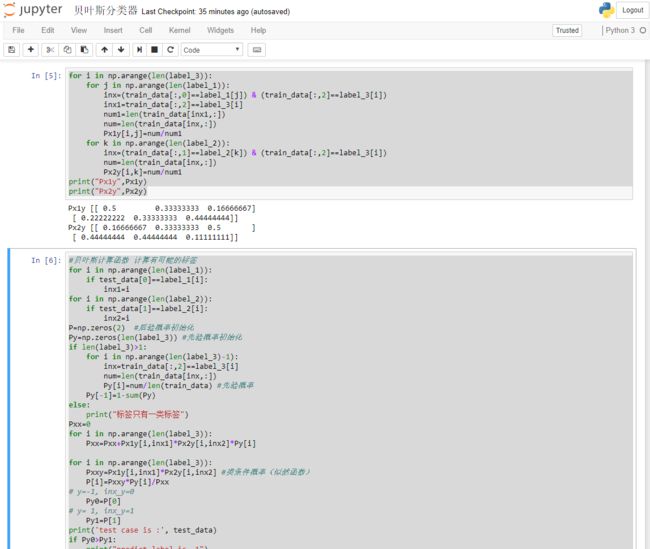
print("Px1y",Px1y)
print("Px2y",Px2y)
#贝叶斯计算函数 计算有可能的标签
for i in np.arange(len(label_1)):
    if test_data[0]==label_1[i]:
        inx1=i
for i in np.arange(len(label_2)):
    if test_data[1]==label_2[i]:
        inx2=i
P=np.zeros(2)  #后验概率初始化
Py=np.zeros(len(label_3)) #先验概率初始化
if len(label_3)>1:
    for i in np.arange(len(label_3)-1):
        inx=train_data[:,2]==label_3[i]
        num=len(train_data[inx,:])
        Py[i]=num/len(train_data) #先验概率
    Py[-1]=1-sum(Py)
else:
    print("标签只有一类标签")
Pxx=0
for i in np.arange(len(label_3)):
    Pxx=Pxx+Px1y[i,inx1]*Px2y[i,inx2]*Py[i]

for i in np.arange(len(label_3)):    
    Pxxy=Px1y[i,inx1]*Px2y[i,inx2] #类条件概率（似然函数）
    P[i]=Pxxy*Py[i]/Pxx
# y=-1, inx_y=0
    Py0=P[0]
# y= 1, inx_y=1 
    Py1=P[1]
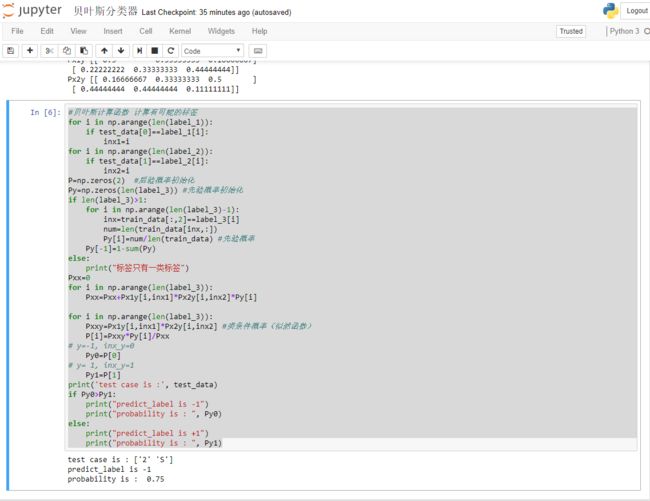
print('test case is :', test_data)
if Py0>Py1:
    print("predict_label is -1")
    print("probability is : ", Py0)
else:
    print("predict_label is +1")
    print("probability is : ", Py1)

程序验证用的样本是[2,"S"]，输出是label:-1。
目前是简单的模型，接下来有机会会引入到实体预测。