深入理解机器学习（一）——二分类模型评价指标详解（上）

当下机器学习领域可谓空前热闹，有不少后起之辈，同时也高手如云。不知道大家有没有见过这样的人，告诉他一些模型指标他就能准确的告诉你当前模型的问题在哪，下一步应该做什么样的实验，宛如会把脉的老中医。怎样学习这样一种能力呢？我注意到很多资料中关于这部分的内容是偏少的。而我刚好在这方面做过一些总结，现在分享出来抛砖引玉。

一、横看成岭侧成峰、远近高低各不同

模型评价通常出现在以下几个环节：调参训练、离线测试、A/B test、线上监控等等。它的意义在于挑出对业务最“有利的”参数或模型。之所以说“最有利”而不是说“最好”，因为模型的评估不是一维的评估。

就像比较两座山，如果是比较哪座更高，结果一目了然。而模型评估是比较哪座山更“雄伟”。如何评价哪座山更“雄伟”呢？山就在那里，我们可以测量它的海拔高度、占地面积、陡峭程度、甚至体积....

正所谓“横看成岭侧成峰，远近高低各不同”，山就在那里，但我们只能通过一些侧面（指标）了解它。如何才能“识得庐山真面目”呢？

二、我们要评估的是什么？

要评价“山”是不是雄伟，我们首先得找到山。模型评估中的山是什么呢？对二分类模型而言，每一个样本都有一个target/label/flag(意思一样啦，都是样本真实类别的标记，同常用0，1表示两个不同的类别)，同时我们可以使用训练好的模型得出一个预测分类pred（假设也是0，1）。这样，我们就有了两个向量，

真实向量：    

预测向量：    

显然，当两个向量a、b相同时最好了，这表示我们的预测与真实标记完全一致。在实际的应用中，通常不会有这么理想的结果。a、b通常存在“差异”，如何衡量这个“差异”的大小呢？我们可以自然的想到一些指标，比如a与b的不同值个数k，不同值的比例，预测为0实际为1的占全部实际为1的比例，等等。是不是想到“山”了？两个向量就在那里，我们可以去看每一对预测和真实标记，但是回头很难有一个准确的印象。不信你看下图，这是随机生成的20个样本：

图1

                  

看完图1告诉我对应的分类器的性能怎么样？哈哈，是不是一头雾水？或者只有一个模糊的印象？

总结：我们的大脑接收信息的方式决定了，想要了解“差异”的全貌，只能通过一些统计指标来描述这个“差异”。统计指标实际上是对信息的压缩。有压缩就有丢失，因此一个单独的指标是片面的，我们通常要综合多个指标来了解“山”的全貌。通过什么样的指标？怎样综合这些指标去还原山的原貌？这是本文的目的。

三、confusion matrix 

confusion matrix 是一种交叉表(cross table)，它用交叉表的形式枚举了预测值pred和target的各种对应情况，把原本的两个向量信息压缩成了一个矩阵。图1中的数据用confusion matrix展示是下面这样的：

图2

我们先说说，pred和targe都有哪几种情况：

预测为1，实际为1：这种情况一般称为True Positive【真阳】，在图2中有8个

预测是1，实际为0：一般称为False Postive【假阳】，在图2中有4个

预测为0，实际为0：一般称为True Negative【真阴】，在图2中有5个

预测为0，实际为1：一般称为Fase Negative【假阴】，在图2中有3个

其中，Postive和Negative的概念是从医学领域引进的，去医院化验过的同学可能会有印象，检测是否患了某种疾病时，化验单上通常会写“阳性”、“阴性”。它表示的是一个判断，Positive/阳性是正向的判断，对于“患有疾病”这个命题它判断为真，Negative/阴性则相反。在机器学习中，Positive和Negative表示的是模型对样本类别的判断/预测。这个预测不总是正确的，当预测正确时我们说这个预测：True。当预测有误时，我们说：Fase。

简单来说：

Positive/Negative表示预测结果

True/False表示预测结果是否正确【注意：不是表示真实值，而是预测值与真实值是否一致！】

 

是不是清晰了很多?我们可以马上口算出预测正确的数量为8+5=13，占总样本的比例为13/20=65%，也就是说模型能准确预测65%的样本，听起来还不错。

 

为了能更便捷的交流，我们对confusion matrix的不同区域给了一些称呼，如下图所示，

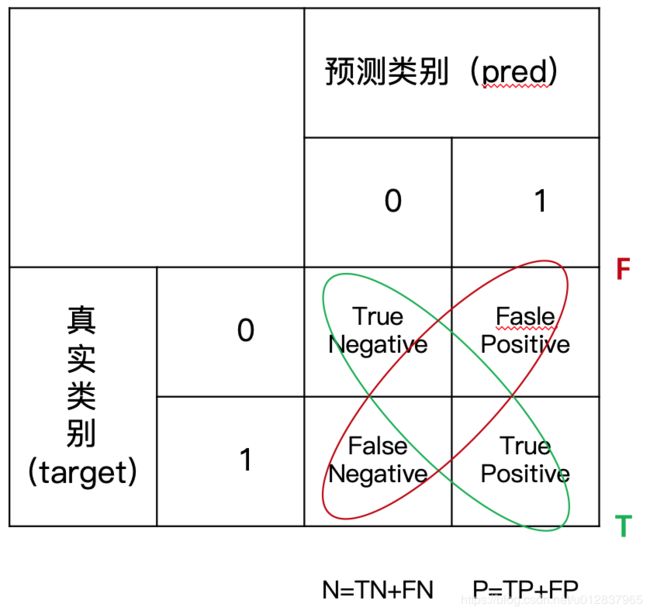图3

对TP(True Positive)、FP、TN、FN的意义，请一定要熟记，这些概念是永远绕不过去的。

 

总结，confusion matrix 是对真实标签和预测信息的第一次压缩。这次压缩我们丢掉了单个样本的信息，把pred和target两个维度都相同的样本无差别的看待，这样我们能够较为直观的感受分类器的性能，比如最简单的：T越大F越小，分类器性能越好。但是这还是不够的。

 

四、基础指标

为了能对分类器的性能有一个更加精确的认识，我们通常在confusion matrix的基础上加工出一些指标。如图4所示：

图4​​

为了方便理解记忆，我对从confusion matrix 可以加工出的指标进行一个分类：“对角指标”、“横向指标”、“纵向指标”，这些是我私自给的定义，并不一定严谨和科学，仅在本文范围内适用。

第一类指标我们称它们“对角指标”（参考图3），它是用预测结果的正确与否进行指标的定义，也是我们第一反应就能想到的指标。

Accuracy是最常用到的指标之一，他能直观的反应分类器性能，但后面我们也会提到当类别不平衡时它会失真。

第二类是“横向指标”，用样本真实类别进行计算的定义：某个区域 / 横向总和。

        很自然的，TPR和FNR的和为1，FPR和TNR的和为1，所有其实这四个指标里，我们只需要知道TPR、FPR就够了，它们也是最常用的，一定要掌握。后面我们会提到ROC曲线、PR曲线，反应的都是这两个指标的关系。

第三类我们称它们“纵向指标”，用预测结果的正类和负类进行计算的定义：某个区域 / 纵向总和。

 

总结，基础指标是对confusion matrix信息的进一步压缩和提炼，他们能更加精确的反应模型的性能，但同时也更加“片面”，后面会看到我们经常成对的使用它们，比如我们希望TPR更高的同时FPR更低。

五、高阶指标

高阶指标是对基础指标的进一步加工，常见高阶指标如下：

缩写	全称	等价称呼	计算公式
LR+	Positive Likelihood Ratio	正类似然比
LR-	Negative likelihood ratio	负类似然比
DOR	Diagnostic odds ratio	诊断胜算比
F1 score	test measure	F1值
MCC	Matthews Correlation coefficient	马修斯相关性系数

F1值是Presision和Recall的调和均值，这些指标里一般掌握它就够了。

 

本篇中提到了一切指标的基础:confusion matrix, 重点提及了4个基础指标和1个高阶指标。这些指标基于预测值是离散的情况，即，非0即1。在更一般的场景下，模型/分类器的预测值通常是一个[0,1]的概率值。在那样的情况下，该如何评估模型呢？下篇文章中将会提到ROC曲线、PR曲线、AUC、KS等图像及指标。