【论文阅读】深度学习去雾1——论文精选

---

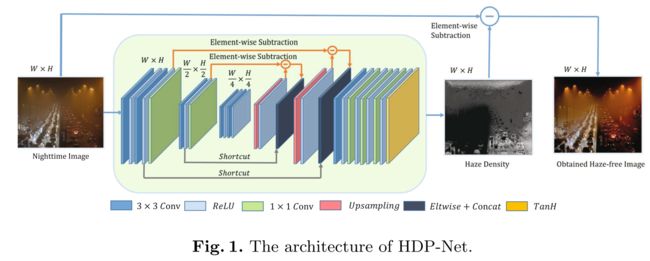
HDP-Net: Haze Density Prediction Network for Nighttime Dehazing

PCM 2018

论文主要不同点是采用不同的物理模型：I = J + H，雾图=无雾图+雾。所以设计了 Haze Density Prediction Network (HDP-Net)进行雾的浓度的预测，输入雾图得到雾的浓度图，然后通过雾图减去浓度图得到最终的无雾图。

物理模型来自于大气散射模型的衍生：

$I_h(x)=I(x)-J(x)$

$I_h(x)=J(x)t(x)+A(1-t(x))-J(x)$

$I_h(x)=(A-J(x))(1-t(x))$

The haze density map could be obtained by extracting the feature value in [ − 1, 1] by CNN。

网络结构

Loss

采用均方误差：$Loss=\sum {\Vert J-\left(I-I_{\text{conv}}\right)\Vert }_2$

ps：
本文的重点是：模型的推理，可以作为一个模型创新应用到daytime dehaze，网络采用的也是简单的网络，并不复杂。但后续跟进发现本文最大的一个问题：训练数据集的问题，这是中山大学的一个工作，但是在数据集合成上，很粗糙，采用的是夜间图片切片，然后深度图采用DCP估计，这不是一个合适的做法。不过目前并没有公开的夜间雾图数据集，这个也算是第一个了，虽然质量真的不好！

---

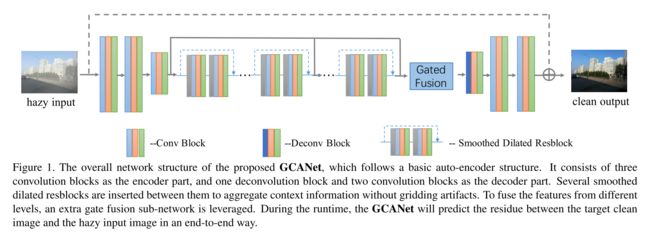
Gated Context Aggregation Network for Image Dehazing and Deraining

WACV 2019

本文的创新点主要是网络架构的两点：1）采用latest smoothed dilation technique 取代dilated convolution以消除网格光晕。2）利用gated fusion sub-network进行不同levels上的feature maps的融合。

其次，本文的网络在deraining任务上也效果出众。

本身创新点看起来一般，但是本文的重点是最终的实验部分数据极其出色，远远高出各种SOTA方法（值得复现）。

网络结构

Loss

本文的学习目标也是雾图和无雾图之间的残差（雾！）
$$\begin{array}{rl}r& =J-I\\ \hat{r}& =GCANet(I)\\ \mathcal{L}& =\Vert \hat{r}-r{\Vert }^2\end{array}$$
Experiments

结果极好！

deraining效果

ablation experiment：各集成的创新点也效果明显。

tricks

• 卷积层后接instance normalization layer和ReLu layer，实验证明instance normalization效果比batch normalization好
• pre-calculated edge information作为辅助信息concatenate到input image上一起输入网络。

ps：1）实验可见gated fusion其实作用不大，倒是instance norm作用明显，考虑其他多尺度融合策略，如CVPR2019提出的HRNet的网络部分。2）Loss Function作者也说了，其他Loss如 the perceptual loss通常是可以增加效果的！3）特征图上的attention机制的尝试（基于全局深度图的考虑，它是需要全局信息的，若没有attention只是局部信息）。

---

Single Image Haze Removal using a Generative Adversarial Network

IET Image Processing 2018

由于IET的审稿周期较长，本文的内容显得有些寻常。

• 提出了单个的CGAN实现端到端去雾。采用54层的Tiramisu Model代替U-Net（这个有效吗?到目前为止大多数low-level task还是在使用U-Net作为生成网络），据文中所说，该模型能提高参数利用率，毕竟实验部分显示该文实验尽然是在笔记本GTX 950M (2GB)上完成的……（吐槽一下这国外的实验室尽然也……，忍不住看看是哪个学校……）
• 采用Patch Discriminator，采用L1 loss + Perceptual loss + cGAN loss 加权结合的总loss，这部分都是来自论文《Image-To-Image Translation With Conditional Adversarial Networks》，作者应该是深受这篇论文影响。

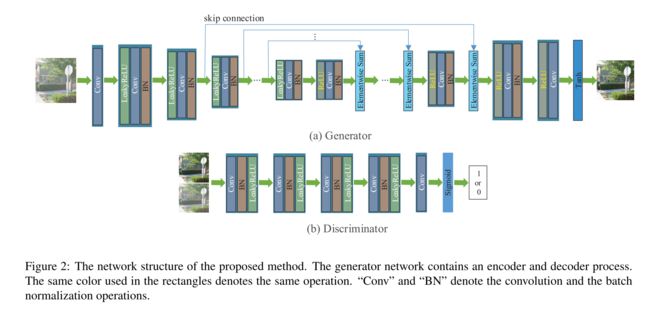
Generator
在原始的U-Net基础上使用 54 Layer Tiramisu （The one hundred layers tiramisu: Fully convolutional densenets for semantic segmentation，CVPRW2017）结构，据说可以加强数据和梯度的流动，训练参数能大大减少（1M）

Discriminator

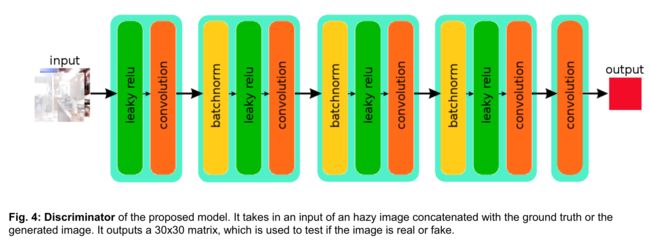
采用原生的Patch GAN（Image-To-Image Translation With Conditional Adversarial Networks，CVPR2017），采用70x70
patch discriminator。This removes a good amount of artefacts in the images。

Input shapes are 256,256,3 for generator and 256,256,6 for the discriminator.

Loss
$$Los{s}_{\text{total}}=W_{gan}\ast L_{Adv}+W_{L1}\ast L_{L1}+W_{vgg}\ast L_{vgg}$$

对抗Loss：
$$L_{Adv}={\mathbb{E}}_{(x,y)}[\log (D(x,y)]+{\mathbb{E}}_{(x,z)}[\log (1-D(x,G(x,z))]$$
Smooth L1 loss：减少光晕，reduce artefacts
$$L_{L1}={\mathbb{E}}_{x,y,z}\left[\Vert y-G(x,z){\Vert }_1\right]$$
Perceptual Loss：VGG-19 network（预训练好的网络，仅用做特征图的loss计算），文中采用的是VGG19的POOL-4输出
$$L_{vgg}=\frac{1}{CWH}\sum _{c=1}^C\sum _{w=1}^W\sum _{h=1}^H{\Vert V\left(\mathrm{G}(x,z{)}^{c,w,h}\right)-V\left(y^{c,w,h}\right)\Vert }_2^2$$
Weight Parameters
$$W_{vgg}=10，W_{gan}=2，W_{L1}=100$$
hyper-parameters

LearningRate=0.001，优化器采用 Adam Optimizer ，设备： Nvidia GTX 950M (2GB) 笔记本

Experiment Results

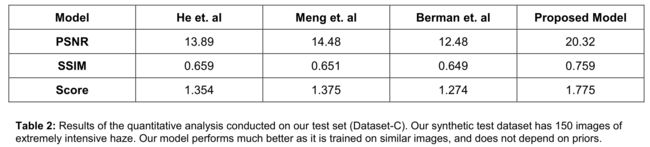
可以看出实验结果强于3个SOTA方法，但是作者也说了是因为其训练样本相似的问题。其实在NYU Depth Dataset上合成图像做去雾，20.32的PSNR忽略其他因素也就和ECCV2017的AOD-Net差不多，所以从实验部分来看，本文其实并没有太多出彩点，实验部分也并没有太多其他的补充，如果在RESIDE数据集上做测试的话，应该也不会强太多（投稿时RESIDE应该还没发布）。

补充说明：上述结果中的Score竟然是作者自己的评分规则，这也是够奇葩的，尽然还通过了评审，貌似TIP 2015专门有一篇文章（Referenceless Prediction of Perceptual Fog Density and Perceptual Image Defogging）提出了一种评价去雾算法的指标，显然会更具说服力。这里的Score是作者自己分配权重的PSNR和SSIM的权重和……
$$Score=W_{PSNR}\ast PSNR+W_{SSIM}\ast SSIM$$
这里PSNR weight = 0.05，SSIM weight = 1.

ps：
本文能说的点不多，主要是多个论文成果的集成应用。值得学习的是在生成网络的去模糊上，采取了3个tricks。L1 loss + Perceptual Loss + Patch GAN，值得一试，不过这也都是原论文提出的。其次，在计算资源有限时，可以试试这个网络（毕竟作者用笔记本训练的）。

---

SC-FEGAN- Face Editing Generative Adversarial Network with User’s Sketch and Color

本文是最近发表在arxiv上的出色的工作，用GAN实现的Face Editing，本身与dehaze无关，关注这片文章主要的切入点是想看看他是如何利用Sketch和Color信息的，因为我的想法是在生成模型中Sketch和Color正好是dehaze task的痛点（雾的结果就是两点：edge lose，color shift），所以从这个角度看，该工作和去雾是有联系的。

效果还是很酷炫的

• 文章的网络结构采用类似的Unet结构+gated convolutional layers。作者认为这种结构对细节很友好。It produced
  superior and detailed result compared to the Coarse-Refined network in our case.
• 在输入中增加了color和sketch
• applied SN-patchGAN discriminator and trained our network with additional style loss。这也对Image details产生作用。

The encoder of our generator receives input tensor of size 512×512×9: an incomplete RGB channel image with a removed region to be edited, a binary sketch that describes the structure of removed parts, a RGB color
stroke map, a binary mask and a noise.

并没有太多关于color和sketch的处理，不过提取color和sketch的过程论文中看起来还是挺麻烦的，需要很仔细阅读其过程。

ps：1）不要以为网络能学到边缘细节，附加的handicraft feature看起来也很重要。2）VGG loss在实验中证明还是很重要的。

---

Perceptually Optimized Generative Adversarial Network for Single Image Dehazing

• 本文同样采用端到端学习的方式，直接学习hazy image到haze-free image的映射。
• 通过GAN模型的生成对抗训练网络。在Discriminator中使用了一种adaptive loss function。
• 提出一种利用guilded filtering进行halo artifacts removal的后处理方法

本文的前两点贡献其实没有多大新意，但是其guilded filtering做去halo的后处理的方式值得借鉴。下图可见其post-processing module效果还是比较明显的。

Loss：GAN中常用的loss
$$l=w_1{l}_{MSE}+w_2{l}_{VGG}+w_3{l}_{Adv}$$
有所不同的是，之前的GAN通常权重w是固定的，本文提出根据不同的haze density采取自适应的权重，即adaptive perceptual loss。

这是由于在大气散射模型中，直接衰减项$\mathbf{J}(x)t(x)$ 表示了雾的浓度，它通常是相关于散射系数$\beta$的。 More specifically, we propose to use larger w1 under heavy haze situation (i.e., more emphasis on haze removal) and larger w3 under light haze condition (i.e., more emphasis on quality assurance).其他类似工作中都采用fixed weights，所以这点到底有没有work不太好说。

halo artifacts removal

看起来效果比较明显，过程如下：

• 从雾图I得到无雾图J1。（此时无雾图J1可以看作是haze-free的，但是存在halo）
• 通过I-J1得到残差r1，此时r1是coarse的，通过guilded filter，得到精细的残差r2（雾图I作为guidance）.
• 最终，J2 = I - r2，J2为最终恢复的无雾图！

过程简单明了。
ps：

• 从实验和原理上来说，本文提出的halo removal方法应该是比较work的，强烈推荐采用！可以尝试改变，比如说guildance不采用I，因为I是边缘弱化的，可以尝试采用去雾后的J1作为guidence，但是可能需要做一些初步处理，因为其本身就是带halo的，任务就是去除它自身的halo。
• 本文的另一个借鉴之处是其实验部分，自己合成了薄雾和厚雾图，区分不同的haze condition来测试算法，比较有说服力！

---

Deep High-Resolution Representation Learning for Human Pose Estimation

CVPR 2019，微软亚洲研究院和中科大提出

本文是Human Pose Estimation方面的最新工作，与dehaze关系不大，但文章提出了一种新颖的网络结果，用以解决当前很多网络中multi-scale feature fusion方法中存在的问题。比如在low-level task中常采用的U-Net就存在多次下采样和上采样操作，在特征空间中，下采样必定意味着后续的特征提取会丢失上层信息，导致下层提取的特征天然缺陷，即使最终concatenate到上层特征图，也不能解决其自身“出身不正”问题。

所以文本的学习切入点主要是网络结构的设计，可以作为dehazing network design中的一个尝试，直观上感觉可能会和attention机制类似，但是attention机制是在当前特征图上相对某个特征元素进行单个特征图的全局的关联，而DHNet（本文提出的网络）结构是在不同分辨率的特征图上进行的交叉关联。

High-Resolution Representation，表达的应该就是特征图中时刻关联着高分辨图中提取的特征。

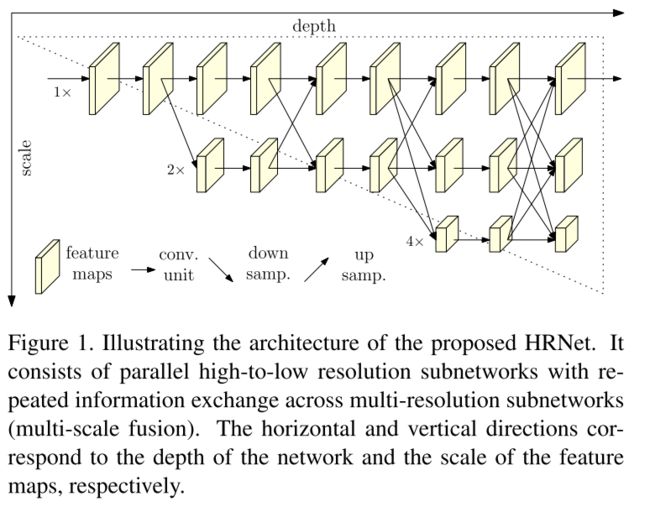
对比已有的网络在不同分辨率特征融合时的操作如下：

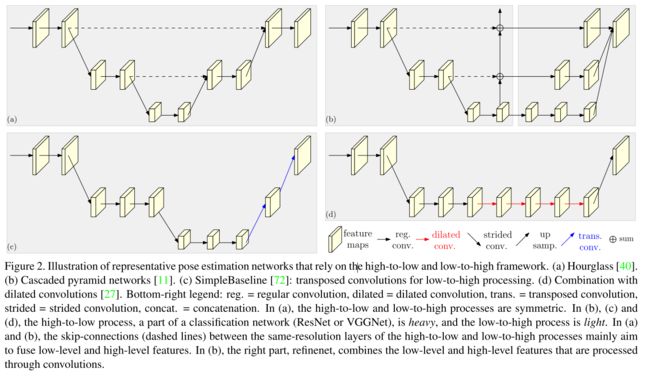
高底层交换信息方法（fusion）

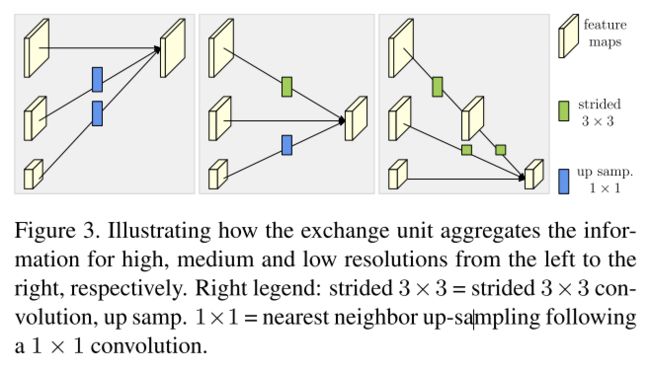
ps：
本文粗读至此，重点在于新的fusion思路的点播，可以在自己的使用中尝试看看会不会work，进一步学习可以仔细琢磨作者的开源代码。

---

Physics-Based Generative Adversarial Models for Image Restoration and Beyond

在许多图像恢复任务中（如deblur、dehaze、deraining），其恢复方式甚至物理模型都具有很大的相似性，同时GAN在处理这些问题时都取得了不错的结果，故本文提出一个统一的模型来解决这类low-level问题：given an input image y, how to estimate a clear image x of the same scene。

如标题所示，本文的动机源于已有的网络往往只关注最终的结果，而不能保证结果是否符合其物理模型。若不符合物理模型约束，得到的结果会在某些局部结构或者细节上出现错误。所以网络同时能还原图像并且保证其符合物理模型就是本文的目标！
实现的方式就是：在原本GAN的基础上，增加一个判别器，用来判别是否符合物理模型，如下图所示

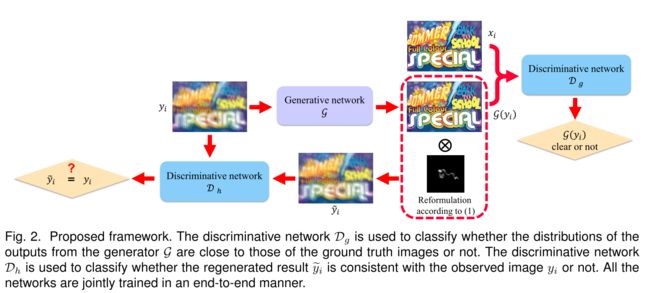
在去雾任务中，Generator产生的去雾图G(yi)先经过普通的Discriminator判断是否去雾（fake or not），再将其通过大气散射模型合成得到雾图，然后通过判别器判别两个雾图是否同分布。这样保证了，正向得到的去雾图是去雾的，逆向，去雾图后的图符合大气散射模型（根据该模型能合成回原来的雾图），细节问题是合成的时候t和A咋办？真实的无标注图像无法用作训练喽？

Loss Function

L1 loss使得生成的haze-free图像接近ground truth，同时generated dehazed image再合成的雾图与原雾图接近。
$${\mathcal{L}}_p=\sum _i{\Vert y_i-y_i\Vert }_1$$

$${\mathcal{L}}_g=\sum _i{\Vert \mathcal{G}\left(y_i\right)-x_i\Vert }_1$$

$${\mathcal{L}}_g=\sum _i{\Vert \mathcal{G}\left(y_i\right)-x_i\Vert }_1$$

这个Loss有点看不懂了，相当于原雾图去雾后的图合成新雾图再去雾得到的结果和ground truth，这也太繁琐了吧……

判别器loss：两个判别器的常规的GAN loss之和，前两项为真伪判别器，后两项为物理模型判别器。
$$\begin{array}{r}{\mathcal{L}}_a=\sum _i\left[\log \left({\mathcal{D}}_g\left(x_i\right)\right)\right]+\left[\log \left(1-{\mathcal{D}}_g\left(\mathcal{G}\left(y_i\right)\right)\right)\right]+\left[\log \left({\mathcal{D}}_h\left(y_i\right)\right)\right]+\left[\log \left(1-{\mathcal{D}}_h\left(y_i\right)\right)\right]\end{array}$$
整体的训练Loss
$$\left({\mathcal{G}}^{\ast },{\mathcal{D}}_g^{\ast },{\mathcal{D}}_h^{\ast }\right)=\underset{\mathcal{G}}{\min }\underset{\mathcal{D}}{\max }\frac{1}{N}\left\{{\mathcal{L}}_a+\lambda \left({\mathcal{L}}_p+{\mathcal{L}}_g+{\mathcal{L}}_g\right)\right\}$$
判别器使用的也是PatchGAN：减少判别器参数，同时效果很好。

ps：
本文最大的两点是多判别器的引入，以及通过判别器实现物理模型约束。

---

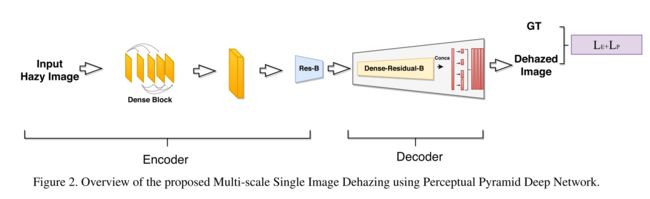
Multi-Scale Single Image Dehazing Using Perceptual Pyramid Deep Network

CVPRW 2018, NTIRE2018-Dehazing Challange

• 首先，和许多相关工作一样，也是采用端到端的直接学习haze image到haze-free的non-linear mapping
• network： multi-scale + Perceptual Pyramid + dense blocks + residual blocks
• encoder-decoder structure with a pyramid pooling module in the decoder to incorporate contextual information of the scene while decoding.
• loss：MSE + perceptual losses
• Multi-scale patches are used during training and inference process to further improve the performance

trick

• patch training：由于NTIRE的数据集分辨率非常高，甚至有些样本超过4k，直接下采样进行训练会损失细节。文章分别裁剪了512X512, 1024X1024, 1024X2048, 2048X2048，以及原始分辨率，再将这些裁剪图resize到640x640进行训练。
• patch inference：indoor和outdoor采用不同策略。大致都是不同的scale 的image patch经过网络得到result patch，然后merge成一个scale上的dehazed result image，最后平均所有的结果图即为最终结果。
• hyper parameter：batchsize=1，lr=0.002，ADAM optimizator

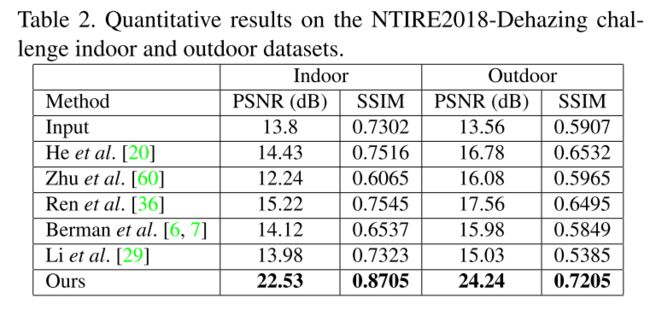
Experiments

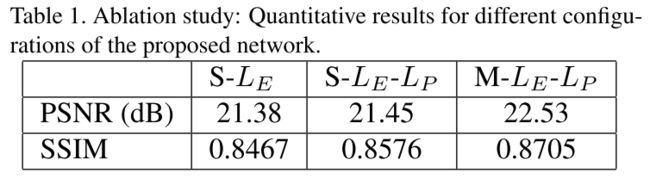
S表示single scale，Le表示MSE loss，Lp表示perceptual loss，M表示Multi-Scale

ps：
本文提供的trick应该是很有效的，尤其是对于高分辨率生成任务！

---

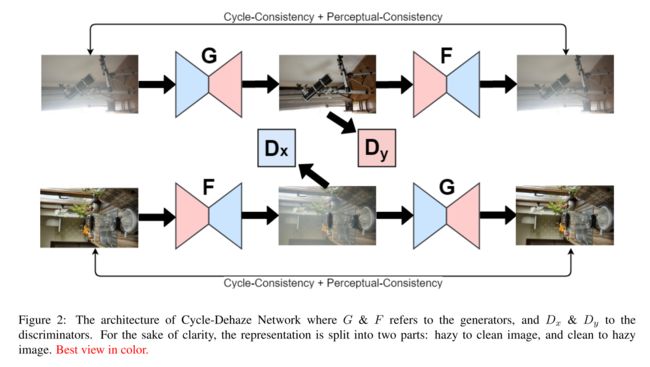
Cycle-Dehaze: Enhanced CycleGAN for Single Image Dehazing

CVPRW 2018, NTIRE2018-Dehazing Challange

本文和前文目标一样，针对高分辨率图像的去雾，但是本文采用的是Cycle-GAN的框架，可以unpair的训练。但是其实结果并不如前文，此处仅单独提出其一些spotlight出来。

• 同样，本文loss也加入了perceptual loss
• 训练的时候，低分辨率input采用bicubic downsample取得，而不像前文PPDN采用patch的方式，感觉patch方式可能work
• 输出高分辨率结果的时候，本文采用Laplacian Pyramid upscale

---

Single Image Dehazing via Conditional Generative Adversarial Network

CVPR 2018

• 采用conditional generative adversarial network，cGAN去雾
• generator采用encoder-decoder结构
• 为了增强生成器效果，引入VGG features（perceptual loss？）以及L1-regularized gradient prior（？？）

（abstract来看，工作的创新点并不是太亮眼，可能在当时时间点上是比较创新的工作）

details and tricks

• skip connections采用summation而不是concatenate，并实验证明了summation的结果优于concatenate

Loss

generator loss：
$$L_A=\frac{1}{N}\sum _{i=1}^N\log \left(1-D\left(I_i,J_i\right)\right)$$

$$L_P=\frac{1}{N}\sum _{i=1}^N{\Vert {\mathcal{F}}_i\left(G\left(I_i\right)\right)-{\mathcal{F}}_i\left(J_i\right)\Vert }_2^2$$

$$L_T=\frac{1}{N}\sum _{i=1}^N\left({\Vert G\left(I_i\right)-J_i\Vert }_1+\lambda {\Vert \nabla G\left(I_i\right)\Vert }_1\right)$$

$$\mathcal{L}=\alpha L_A+\beta L_P+\gamma L_T$$

其中，$\alpha =1,\beta =150,\gamma =150,\lambda =10^{-5}$

Discriminator loss：
$$\underset{D}{\max }\frac{1}{N}\sum _{i=1}^N\left(\log \left(1-D\left(I_i,J_i\right)\right)+\log \left(D\left(I_i,J_i\right)\right)\right)$$

实验结果：

---

Towards Perceptual Image Dehazing by Physics-Based Disentanglement and Adversarial Training

AAAI 2018

和Cycle-Dehaze类似，采用CycleGAN策略实现unpair的训练。

创新点：多尺度的discrimination loss（文中采用的尺度为70x70, 256x256，两个尺度上的D loss）

The classical GAN loss can be described as:
$${\mathcal{L}}_{GAN}(G,D)={\mathbb{E}}_{J\sim \mathcal{J}}[\log D(J)]+{\mathbb{E}}_{I\sim \mathcal{I}}[\log (1-D(G(I)))]$$
本文提出的loss：
$${\mathcal{L}}_{adv}\left(G_J,D\right)=\frac{1}{2}\left({\mathcal{L}}_{GAN}\left(G_J,D^{loc}\right)+{\mathcal{L}}_{GAN}\left(G_J,D^{glo}\right)\right)$$
原理图：

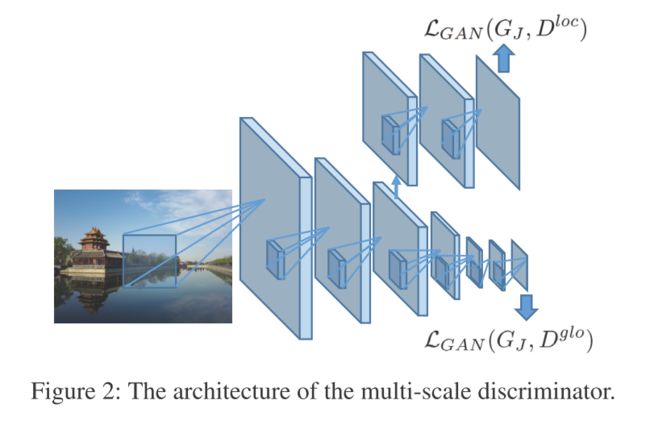
可以作为一个增强discriminator的trick

本文的loss还是有些不同的

• reconstruction loss：并没有采用常见的L2 loss，原文解释是encourage both pixel-level consistency and less blurring (compared with L2 loss)，其采用的L1 loss。
  $${\mathcal{L}}_{recon}\left(G_J,G_t,G_A\right)={\mathbb{E}}_{I\sim I}\Vert I-\hat{I}{\Vert }_1$$

• GAN loss采用的是上述multi-scale adversarial loss
  $${\mathcal{L}}_{adv}\left(G_J,D\right)=\frac{1}{2}\left({\mathcal{L}}_{GAN}\left(G_J,D^{loc}\right)+{\mathcal{L}}_{GAN}\left(G_J,D^{glo}\right)\right)$$

• 同时加入了一个正则loss，用来平滑图像， total variation loss，常用于style-transfer（https://github.com/CortexFoundation/StyleTransferTrilogy）
  $${\mathcal{L}}_{reg}\left(G_t\right)=TV(t)=\sum _{i,j}\left|t_{i+1,j}-t_{i,j}\right|+\left|t_{i,j+1}-t_{i,j}\right|$$

• 最终的loss为：
  $$\begin{array}{r}\mathcal{L}\left(G_J,G_t,G_A,D\right)={\mathcal{L}}_{adv}\left(G_J,D\right)+\lambda {\mathcal{L}}_{recon}\left(G_J,G_t,G_A\right)+\gamma {\mathcal{L}}_{reg}\left(G_t\right)\end{array}$$
  实验中的权重参数为：（文章竟然没给权重参数……）

Results

ps：
Loss有待具体实验，但多尺度判别器loss的想法很不错，可以进一步考虑。