快速傅里叶变换学习及C语言实现
将之前学过的知识重新拾起来,仔细理解并实现。
参考:《算法导论》第30章
从头到尾彻底理解傅里叶变换算法、上
Cooley–Tukey FFT algorithm
FFT(快速傅里叶) c语言版
数字信号处理–FFT与蝶形算法
在线MATLAB
一、引言
首先回顾信号与系统的知识,傅里叶变换是一种从时间域转换到频率域的变换,下面列出的几种变体。
| 变换 | 时域 | 频域 |
|---|---|---|
| 连续傅里叶变换(FT) | 连续、非周期 | 非周期、离散 |
| 傅里叶级数 | 连续、周期 | 非周期、离散 |
| 离散时间傅里叶变换(DTFT) | 离散、非周期 | 周期、连续 |
| 离散傅里叶变换(DFT) | 离散、周期 | 周期、离散 |
通过表格后两列可以发现:
时域的周期对应频域的离散、时域的连续对应频域的非周期,反过来也是如此。
一个域的周期对应另一个域离散、一个域的连续对应另一个域的非周期
连续傅里叶变换
连续傅里叶变换将平方可积的函数f(t)表示成复指函数的积分或者级数形式。
傅里叶级数
连续形式的傅里叶变换其实是傅里叶级数的推广,因为积分其实是一种极限形式的求和算子。对于周期函数,其傅里叶级数是存在的。
离散时域傅里叶变换
离散时域傅里叶变换DTFT在时域是离散的,在频域是周期的。DTFT可以看做是傅里叶级数的逆变换。
离散傅里叶变换
离散傅里叶变换DFT是连续傅里叶变换在时域和频域都离散的。同时在时域和频谱序列通常是有限长的,实际上将他们认为是离散周期信号的主值序列,对其进行周期延拓即可得到周期信号。
为了在科学计算和数字信号处理等领域使用计算机进行傅里叶变换,必须将输入定义在离散点而非连续域内,且须满足有限性或周期性条件。这是使用离散傅里叶变换DFT的原因。

离散傅里叶变换可以将连续的频谱转化成离散的频谱去计算,这样就易于计算机编程实现。时间复杂度O(n^2)。
进而引出下文,快速傅里叶变换FFT的出现,使得DFT的计算速度更快。时间复杂度O(nlgn)。
二、快速傅里叶变换FFT
快速傅立叶变换(Fast Fourier Transform,FFT)是离散傅立叶变换(Discrete Fourier transform,DFT)的快速算法,它是根据离散傅立叶变换的奇、偶、虚、实等特性,对离散傅立叶变换的算法进行改进获得的。它对傅立叶变换的理论并没有新的发现,但是对于在计算机系统或者说数字系统中应用离散傅立叶变换,可以说是进了一大步。
设 Xn 为 N 项的复数序列,由 DFT 变换,任一 Xi 的计算都需要 N 次复数乘法和 N -1 次复数加法,而一次复数乘法等于四次实数乘法和两次实数加法,一次复数加法等于两次实数加法,即使把一次复数乘法和一次复数加法定义成一次“运算”(四次实数乘法和四次实数加法),那么求出 N 项复数序列的 Xi ,即 N 点 DFT 变换大约就需要 N^2 次运算。
举例:当 N =1024 点的时候,
使用DFT,需要 N^2 = 1048576 次运算。
使用 FFT ,利用 ωn 的周期性和对称性,把一个 N 项序列(设 N 为偶数),分为两个 N / 2 项的子序列,每个 N / 2点 DFT 变换需要 (N / 2)^2 次运算,再用 N 次运算把两个 N / 2点的 DFT 变换组合成一个 N 点的 DFT 变换。这样变换以后,总的运算次数就变成 N + 2 * (N / 2)^2 = N + N^2 / 2。当N =1024 时,总的运算次数就变成了525312 次。
二者对比可以看到,节省了大约 50% 的运算量。
而如果我们将这种“一分为二”的思想不断进行下去,直到分成两两一组的 DFT 运算单元,那么N 点的 DFT 变换就只需要 N * log2N 次的运算,N = 1024 点时,运算量仅有 10240 次,是先前的直接算法的1% ,点数越多,运算量的节约就越大,这就是 FFT 的优越性。
基2 DIT公式推导
核心:FFT算法是把长序列的DFT逐次分解为较短序列的DFT。

综合以上推导我们可以得到如下结论:一个N点的DFT变换过程可以用两个N/2点的DFT变换过程来表示。
上式中Ek为偶数项分支的离散傅立叶变换,Ok为奇数项分支的离散傅立叶变换。其中的一个计算单元可以使用蝶形算法流图直观地表示出来。
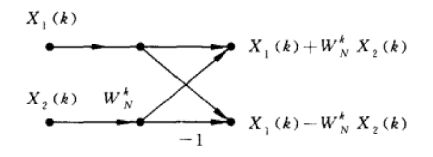
那么在实现时步骤如下:
- 将N点的输入序列按奇偶分为2组分别为N/2点的序列
- 分别对每组序列进行DFT变换得到两组点数为N/2的DFT变换值X1和X2
- 按照蝶形信号流图将2的结果组合为一个N点的DFT变换结果
三、快速傅里叶变换递归实现
类似于归并排序,采用分治算法自定向下进行将问题划分为同等规模的小问题。
FFT 的实现也可以自顶而下,采用递归实现。

参考了官网的代码,进行8点FFT的实现:
//g++ fft.cpp -o fft -lm
#include 四、快速傅里叶变换迭代实现
FFT 的实现可以自顶而下,采用递归,但是对于硬件实现成本高,对于软件实现都不够高效,改用迭代较好,自底而上地解决问题。感觉和归并排序的迭代版很类似,不过先要采用“位反转置换”的方法把 Xi 放到合适的位置。
位反转算法- 雷德算法
一个小算法的感觉。
拿一个0到2^n-1的自然数序列。
比方说
0 1 2 3 4 5 6 7
我们转换为二进制状态,那么这个序列就是
000 001 010 011 100 101 110 111
接下来我们模拟FFT的位置交换,即:
0 1 2 3 4 5 6 7
0 2 4 6 1 3 5 7
0 4 2 6 1 5 3 7
发现最终的序列变为了
000 100 010 110 001 101 011 111
雷德算法就是用于求出这个倒序的数列。
由上面的表可以看出,按自然顺序排列的二进制数,其后面一个数总是比其前面一个数大1,即后面一个数是前面一个数在最低位加1并向高位进位而得到的。
而倒位序二进制数的后面一个数是前面一个数在最高位加1并由高位向低位进位而得到。
I、J都是从0开始,若已知某个倒位序J,要求下一个倒位序数:
应先判断J的最高位是否为0。
这可与k=N/2相比较,因为N/2总是等于100的。
如果k>J,则J的最高位为0,只要把该位变为1(J与k=N/2相加即可),就得到下一个倒位序数;
如果K<=J,则J的最高位为1,可将最高位变为0(J与k=N/2相减即可)。然后还需判断次高位,这可与k=N\4相比较,若次高位为0,
则需将它变为1(加N\4即可)其他位不变,既得到下一个倒位序数;若次高位是1,则需将它也变为0。然后再判断下一位……
代码实现:
//假设N为2的整数次幂
void RaderReverse(int *arr, int N) {
int j,k;
//第一个和最后一个数位置不变,故不处理
for(int i=1,j=N/2; i<N-1; ++i) {
//原始坐标小于变换坐标才交换,防止重复
if(i<j) {
int temp = arr[j];
arr[j] = arr[i];
arr[i] = temp;
}
k = N/2; // 用于比较最高位
while(k <= j) { // 位判断为1
j = j-k;// 该位变为0
k = k/2;// 用于比较下一高位
}
j = j+k;// 判断为0的位变为1
}
}
时间抽取 DIT Radix-2算法

该算法的特征是:
1)输入序列顺序位反转,输出所有频率值都是按顺序出现的。
2)计算可以“就地”完成,也就是蝶形所使用的存储位置可以被重写。
3)从图中我们可以看到对于点数为N = 2^L的FFT运算,可以分解为L阶蝶形图级联,每一阶蝶形图内又分为M个蝶形组,每个蝶形组内包含K个蝶形。(迭代算法实现:根据这一点我们就可以构造三阶循环来实现蝶形运算。编程过程需要注意旋转因子与蝶形阶数和蝶形分组内的蝶形个数存在关联。)

快速傅里叶变换迭代算法实现
该代码在上文的基础上,参考了FFT(快速傅里叶) c语言版的思想。
代码实现:
//g++ fft2.cpp -o fft2 -lm
#include
// printf("%0.3f \t %0.3f\n",X[i].real(),X[i].imag());
fft(X,nSamples);
for(int i=0; i<nSamples; ++i )
printf("%0.3f \t %0.3f\n",X[i].real(),X[i].imag());
}