数据结构—图I
图的基本概念
1. 图的定义
图G是由顶点集V和边集E组成,记为G=(V,E),其中V(G)表示图中的非空有限集。
【注】线性表和树都可以为空,但是图不可以为空。
2. 图基本概念和术语
弧:表示有向图中的边。
完全图:图中任意两个顶点(图中称之为顶点,树中叫结点)之间都存在边。含有n个顶点的无向完全图含有 n(n-1)/2 条边。含有n个顶点的有向完全图有 n(n-1) 条有向边。
连通,连通图,连通分量:
在无向图中,若顶点v到顶点w有路径存在,则称v和w是连通的。若图中任意 两个顶点都是连通的(这里指的是有路径存在,区分完全图中的直接相连), 则称图 G为连通图。无向图中的极大【notmax】连通子图称为连通分量。
【注】极大连通子图是无向图中的连通分量,极大即要求该连通子图包括其所有边(子图所拥有的); 极小连通子图是既要保持图畅通,又要使得边数最少的子图;极小连通子图就是之后连通图的生成树。
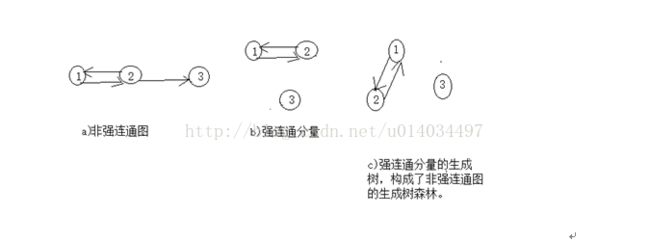
强连通图和强连通分量是只对有向图的,无向图中一般讨论连通性。
生成树,生成森林:
连通图的生成树是包含图中全部顶点的一个极小连通子图。若图中顶点树为n,则它的生成树含有n-1条边。在非连通图中,(强)连通分量的生成树构成了非(强)连通图的全部森林。
顶点的度,出度和入度
在具有n个顶点e条边的无向图中,TD(vi)=2e。即无向图全部顶点的度之和等于边数的两倍。这是因为每条边和两个顶点相连。
对于有向图,顶点v的度分为入度和出度。这里顶点的度等于其入度加出度。即TD(v)=ID(v)+OD(v)。在具有n个顶点e条边的有向图中。.即有向图的全部顶点的出度等于入度,并且等于边数。这是因为每条有向边都有一个起点和终点。
带权图也称作网
稠密图,稀疏图:根据边数的相对多少。一般当图G满足E
路径,路径长度和回路
路径是指顶点和相邻顶点序偶构成的边所形成的序列。 第一个顶点和最后一个顶点相同的路径称为回路或环。路径上边的数目称为路径长度。
【注】如果一个图有n个顶点,并且有大于n-1条边,则此图一定有回路(此时即为连通图)
简单路径,简单回路
在路径序列中,顶点不重复出现的路径称为简单路径;除第一个和最后一个之外,其余顶点不重复出现的回路称为简单回路。
有向树:有一个顶点的入度为0其余顶点入度均为1的有向图称作有向树。
一些特殊结论:
1. 对于连通无向图,边最少构成一棵树的情形;对于强连通有向图,边最少即构成一个有向环的情形,即只有两个顶点相互指向。
图的存储及及基本操作
1. 存储方式:邻接矩阵法和邻接表,前者是顺序存储结构,后者是链接存储结构。
2. 邻接矩阵存储:就是用一个一维数组存储图中顶点信息,用一个二维数组存储图中边的信息(此称其为邻接矩阵)。
,
【注】
l 因此,邻接矩阵的规律,无向图的是一对称矩阵(01对称分布);有向图的是一简单矩阵(01非对称分布);带权图(网)的是一带权矩阵(矩阵中元素值为各条边的权重,0,表示彼此不可通)。
l 对于无向图,邻接矩阵的第i行(或i列)非零元素(或非元素)个数正好是第i个顶点的度TD(i)。 因为其入度等于出度嘛。
l 对于有向图,邻接矩阵的第i行(或i列)非零元素(或非元素)个数正好是第i个顶点的出度OD(i)(或入度ID(i))。 数组下标结构特点决定。
l 评估:很容易确定任意两个顶点之间是否有边相连(O(1)复杂度)。但缺点是要确定有多少条边却需要O(n^2)时间复杂度。
3. 邻接表存储:
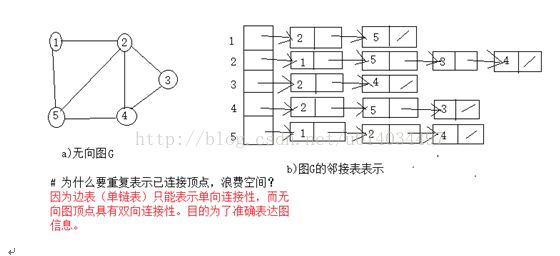
【引】 稀疏图时,邻接矩阵表示法显然很浪费空间。而图的邻接表法结合了顺序存储和链式存储,大大减少了这种浪费。
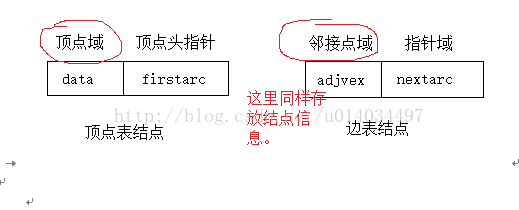
邻接表定义:对图G中每个顶点Vi都建立一个单链表,表示依附于顶点Vi的边(对于有向图则是以顶点Vi为尾的弧),称之为顶点Vi的边表(对应有向图称之为出边表)。
边表的头指针和顶点的数据信息采用顺序存储(称为顶点表),所以在邻接表中存在两种结点:顶点表结点和边表结点。
【补充】而且边表邻接顶点域可只存图G中顶点标号,以节省空间。
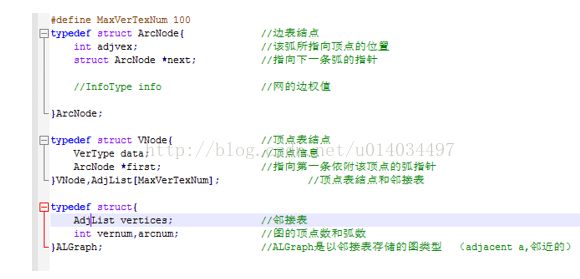
邻接表代码定义:
【特征】
l 如果G为无向图,则需存储空间O(V+2E);如果为有向图,则所需存储空间为O(V+E)
l 在邻接表中,给一顶点,读取它的邻接表就可以找到其所有邻边,花费O(L),而邻接矩阵中,需花费O(n)。 但是如果要确定两个顶点间是否存在边,邻接矩阵花费O(1)时间,邻接表则O(2L)时间(无向图O(L))。 其中L为边表长度
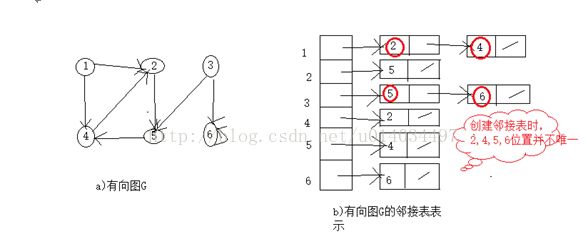
l 在有向图的邻接表中,求一个顶点的出度只需计算其邻接表中结点个数,时间花费O(L)。但是求入度,则需要遍历全部的邻接表,时间花费O(E)。
l 图的邻接表表示并不唯一,这是因为在每个对应的单链表中,各边结点的链接次序可以是任意的,取决于建立邻接表的算法和边的输入次序。
4 图的基本操作
图的基本操作是独立于图的存储结构的。这句话有着深深的含义,操作建立在抽象的数据结构上。
而对于不同的存储方式,操作算法的具体实现会有着不同的性能。
常用的有:
FirstNeighbor(G,x)
NextNeighbor(G,x,y) //假设图G中顶点y是顶点x的一个邻接点,返回出y之外顶点x的下一个邻接点的顶点号。若不存在,返回-1