决策树相关算法——XGBoost原理分析及实例实现(三)
1前言
本篇博客作为前两篇XGBoost的原理与分析的续作三,主要记录的是使用XGBoost对kaggle中的初级赛题Titanic: Machine Learning from Disaster进行预测的实例,以此来加深自己对XGBoost库的使用。
前两篇XGBoost原理分析如下,本篇实例地址为Github
决策树相关算法——XGBoost原理分析及实例实现(一)
决策树相关算法——XGBoost原理分析及实例实现(二)
2数据集分析
Titanic赛题的数据集需要到上述赛题地址下载,包括训练集train.csv中,测试集test.csv,最后赛题预测的答案集为gender_submission.csv。
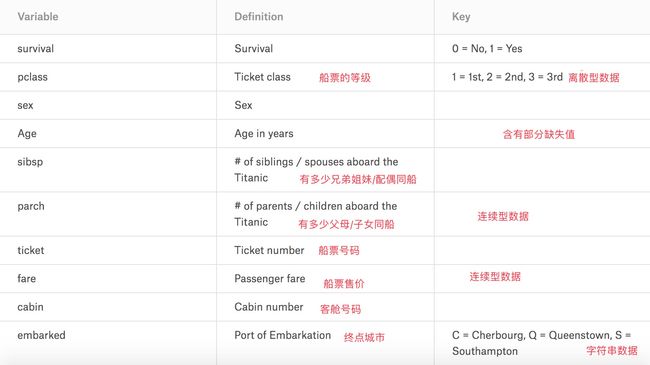
给出的数据集的记录中有些Variable存在缺失,而且Variable的值存在离散型数据,连续型数据和字符串数据。这些在训练模型之前都需要进行处理,首先对赛题给出的数据进行分析,提取出要训练的模型特征。
3特征工程
此赛题的特征工程主要包括四个任务:数据缺失值处理,连续型数据特征值处理,字符串型数据特征值处理,预测模型的特征选择。接下来这3个任务将贯穿整个特征工程的过程。
特征选择一般的方式有:计算每一个特征与响应变量label的相关性,比如说计算互信息系数。训练能够对特征打分的预选模型:RandomForest和Logistic Regression等都能对模型的特征打分,通过打分获得相关性后再训练最终模型;
3.1查看数据整体信息
包括行列信息,各列Variable缺失值情况,dtypes的值。
###### in
import numpy as np
import pandas as pd
train = pd.read_csv("ML/data/Titanic/train.csv")
test = pd.read_csv("ML/data/Titanic/test.csv")
full_data = [train,test]
print(train.info())
###### out
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 891 entries, 0 to 890
Data columns (total 12 columns):
PassengerId 891 non-null int64
Survived 891 non-null int64
Pclass 891 non-null int64
Name 891 non-null object
Sex 891 non-null object
Age 714 non-null float64
SibSp 891 non-null int64
Parch 891 non-null int64
Ticket 891 non-null object
Fare 891 non-null float64
Cabin 204 non-null object
Embarked 889 non-null object
dtypes: float64(2), int64(5), object(5)
memory usage: 83.6+ KB
None
3.2根据train.csv中各个Variable的取值和特性进行数据处理
主要查看数据的各个Variable对Survived的影响来确定是否该Variable对生还有影响。分析代码地址
1.PassengerId 和 Survived
Survived是模型最终需要预测的Label,给定的数据集该Variable值没有缺失。PassengerId是各个乘客的ID,每个ID号各不相同,基本没有什么数据挖掘意义,对需要预测的存活性几乎没有影响。
2.Pclass
pclass为船票类型,离散数据(不需要进行特别处理),没有缺失值。该变量的取值情况如下。
###### in
print (train['Pclass'].value_counts(sort=False).sort_index())
###### out
1 216
2 184
3 491
###### Pclass和Survived的影响
#计算出每个Pclass属性的取值中存活的人的比例
print train[['Pclass','Survived']].groupby('Pclass',as_index=False).mean()
###### out
Pclass Survived
0 1 0.629630
1 2 0.472826
2 3 0.242363
从输出的生还率可以看出,不同的Pclass类型对生还率影响还是很大的,所以选取该属性作为最终的模型的特征之一,取值为1,2,3.
3.Sex
Sex为性别,连续型数据特征,没有缺失值。该变量的取值情况如下。
###### in
print (train['Sex'].value_counts(sort=False).sort_index())
###### out
female 314
male 577
###### Sex和Survived的影响
#计算出每个Sex属性的取值中存活的人的比例
print train[['Sex','Survived']].groupby('Sex',as_index=False).mean()
###### out
Sex Survived
0 female 0.742038
1 male 0.188908
从输出的生还率可以看出,不同的Sex类型对生还率影响还是很大的,所以选取该属性作为最终的模型.对于字符串数据特征值的处理,可以将两个字符串值映射到两个数值0,1上。
4.Age
Age为年龄,连续型数据,Age 714 non-null float64该属性包含较多的缺失值,不宜删除缺失值所在的行的数据记录。此处不仅需要对缺失值进行处理,而且需要对该连续型数据进行处理。
1.对于该属性的缺失值处理:方法一,默认填充值的范围[(mean - std) ,(mean + std)]。方法二,将缺失的Age当做label,将其他列的属性当做特征,通过已有的Age的记录训练模型,来预测缺失的Age值。
2.对该连续型数据进行处理:常用的方法有两种,方法一,等距离划分。方法二,通过卡方检验/信息增益/GINI系数寻找差异较大的分裂点。
###对于该属性的缺失值处理方式一,方式二在最终的代码仓库中
for dataset in full_data:
age_avg = dataset['Age'].mean()
age_std = dataset['Age'].std()
age_null_count = dataset['Age'].isnull().sum()
age_default_list = np.random.randint(low=age_avg-age_std,high=age_avg+age_std,size=age_null_count,)
dataset['Age'][np.isnan(dataset['Age'])] = age_default_list
dataset['Age'] = dataset['Age'].astype(int)
###对该连续型数据进行处理方式二
train['CategoricalAge'] = pd.cut(train['Age'], 5)
print (train[['CategoricalAge', 'Survived']].groupby(['CategoricalAge'], as_index=False).mean())
###### out
CategoricalAge Survived
0 (-0.08, 16.0] 0.532710
1 (16.0, 32.0] 0.360802
2 (32.0, 48.0] 0.360784
3 (48.0, 64.0] 0.434783
4 (64.0, 80.0] 0.090909
可以看出对连续型特征Age离散化处理后,各个年龄阶段的存活率还是有差异的,所以可以选取CategoricalAge作为最终模型的一个特征。
5.SibSp and Parch
SibSp和Parch分别为同船的兄弟姐妹和父母子女数,离散数据,没有缺失值。于是可以根据该人的家庭情况组合出不同的特征。
###### SibSp对Survived的影响
print train[['SibSp','Survived']].groupby('SibSp',as_index=False).mean()
###### Parch对Survived的影响
print train[['Parch','Survived']].groupby('Parch',as_index=False).mean()
###### Parch和SibSp组合对Survived的影响
for dataset in full_data:
dataset['FamilySize'] = dataset['SibSp'] + dataset['Parch'] + 1
print (train[['FamilySize', 'Survived']].groupby(['FamilySize'], as_index=False).mean())
###### 是否为一个人IsAlone对Survived的影响
train['IsAlone'] = 0
train.loc[train['FamilySize']==1,'IsAlone'] = 1
print (train[['IsAlone', 'Survived']].groupby(['IsAlone'], as_index=False).mean())
###### out 1
SibSp Survived
0 0 0.345395
1 1 0.535885
2 2 0.464286
3 3 0.250000
4 4 0.166667
5 5 0.000000
6 8 0.000000
###### out 2
Parch Survived
0 0 0.343658
1 1 0.550847
2 2 0.500000
3 3 0.600000
4 4 0.000000
5 5 0.200000
6 6 0.000000
###### out 3
0 1 0.303538
1 2 0.552795
2 3 0.578431
3 4 0.724138
4 5 0.200000
5 6 0.136364
6 7 0.333333
7 8 0.000000
8 11 0.000000
###### out 4
IsAlone Survived
0 0 0.505650
1 1 0.303538
从输出的生还率可以看出,可以选取的模型特征有Parch和SibSp组合特征FamilySize,Parch,SibSp,IsAlone该四个特征的取值都为离散值。
6.Ticket和Cabin
Ticket为船票号码,每个ID的船票号不同,难以进行数据挖掘,所以该列可以舍弃。Cabin为客舱号码,204 non-null object对于891条数据记录来说,缺失巨大,难以进行填充或者说进行缺失值补充带来的噪音将更多,所以可以考虑放弃该列。
7.Fare
Fare为船票售价,连续型数据,没有缺失值,需要对该属性值进行离散化处理。
for dataset in full_data:
dataset['Fare'] = dataset['Fare'].fillna(train['Fare'].median())
train['CategoricalFare'] = pd.qcut(train['Fare'],6)
print (train[['CategoricalFare', 'Survived']].groupby(['CategoricalFare'], as_index=False).mean())
###### out
CategoricalFare Survived
0 (-0.001, 7.775] 0.205128
1 (7.775, 8.662] 0.190789
2 (8.662, 14.454] 0.366906
3 (14.454, 26.0] 0.436242
4 (26.0, 52.369] 0.417808
5 (52.369, 512.329] 0.697987
可以看出对连续型特征Fare离散化处理后,各个票价阶段的存活率还是有差异的,所以可以选取CategoricalFare作为最终模型的一个特征。此时分为了6个等样本数阶段。
8.Embarked
Embarked是终点城市,字符串型特征值,889 non-null object对于891个数据记录来说,缺失数极小,所以这里考虑使用该属性最多的值填充。
print (train['Embarked'].value_counts(sort=False).sort_index())
###### out
C 168
Q 77
S 644
Name: Embarked, dtype: int64
#### 填充和探索Embarked对Survived的影响
for data in full_data:
data['Embarked'] = data['Embarked'].fillna('S')
print (train['Embarked'].value_counts(sort=False).sort_index())
print (train[['Embarked', 'Survived']].groupby(['Embarked'], as_index=False).mean())
###### out1
C 168
Q 77
S 646
Name: Embarked, dtype: int64
Embarked Survived
0 C 0.553571
1 Q 0.389610
2 S 0.339009
可以看出不同的Embarked类型对存活率的影响有差异,所以可以选择该列作为最终模型的特征,由于该属性的值是字符型,还需要进行映射处理或者one-hot处理。
9.Name
Name为姓名,字符型特征值,没有缺失值,需要对字符型特征值进行处理。但是观察到Name的取值都是不相同,但其中发现Name的title name是存在类别的关系的。于是可以对Name进行提取出称呼这一类别title name.
import re
def get_title_name(name):
title_s = re.search(' ([A-Za-z]+)\.', name)
if title_s:
return title_s.group(1)
return ""
for dataset in full_data:
dataset['TitleName'] = dataset['Name'].apply(get_title_name)
print(pd.crosstab(train['TitleName'],train['Sex']))
###### out
Sex female male
TitleName
Capt 0 1
Col 0 2
Countess 1 0
Don 0 1
Dr 1 6
Jonkheer 0 1
Lady 1 0
Major 0 2
Master 0 40
Miss 182 0
Mlle 2 0
Mme 1 0
Mr 0 517
Mrs 125 0
Ms 1 0
Rev 0 6
Sir 0 1
####可以看出不同的titlename中男女还是有区别的。进一步探索titlename对Survived的影响。
####看出上面的离散取值范围还是比较多,所以可以将较少的几类归为一个类别。
train['TitleName'] = train['TitleName'].replace('Mme', 'Mrs')
train['TitleName'] = train['TitleName'].replace('Mlle', 'Miss')
train['TitleName'] = train['TitleName'].replace('Ms', 'Miss')
train['TitleName'] = train['TitleName'].replace(['Lady', 'Countess','Capt', 'Col',\
'Don', 'Dr', 'Major', 'Rev', 'Sir', 'Jonkheer', 'Dona'], 'Other')
print (train[['TitleName', 'Survived']].groupby(['TitleName'], as_index=False).mean())
###### out1
TitleName Survived
0 Master 0.575000
1 Miss 0.702703
2 Mr 0.156673
3 Mrs 0.793651
4 Other 0.347826
可以看出TitleName对存活率还是有影响差异的,TitleName总共为了5个类别:Mrs,Miss,Master,Mr,Other。
3.3赛题的特征提取总结
此赛题是计算每一个属性与响应变量label的影响(存活率)来查看是否选择该属性作为最后模型的输入特征。最后选取出的模型输入特征有Pclass,Sex,CategoricalAge,FamilySize,Parch,SibSp,IsAlone,CategoricalFare,Embarked,TitleName。
最后对上述分析进行统一的数据清洗,将train.csv和test.csv统一进行处理,得出新的模型训练样本集。
4XGBoost模型训练
4.1数据清洗和特征选择
此步骤主要是根据3中的数据分析来进行编写的。着重点Age的缺失值使用了两种方式进行填充。均值和通过其他清洗的数据特征使用随机森林预测缺失值两种方式。
def data_feature_engineering(full_data,age_default_avg=True,one_hot=True):
"""
:param full_data:全部数据集包括train,test
:param age_default_avg:age默认填充方式,是否使用平均值进行填充
:param one_hot: Embarked字符处理是否是one_hot编码还是映射处理
:return: 处理好的数据集
"""
for dataset in full_data:
# Pclass、Parch、SibSp不需要处理
# sex 0,1
dataset['Sex'] = dataset['Sex'].map(Passenger_sex).astype(int)
# FamilySize
dataset['FamilySize'] = dataset['SibSp'] + dataset['Parch'] + 1
# IsAlone
dataset['IsAlone'] = 0
isAlone_mask = dataset['FamilySize'] == 1
dataset.loc[isAlone_mask, 'IsAlone'] = 1
# Fare 离散化处理,6个阶段
fare_median = dataset['Fare'].median()
dataset['CategoricalFare'] = dataset['Fare'].fillna(fare_median)
dataset['CategoricalFare'] = pd.qcut(dataset['CategoricalFare'],6,labels=[0,1,2,3,4,5])
# Embarked映射处理,one-hot编码,极少部分缺失值处理
dataset['Embarked'] = dataset['Embarked'].fillna('S')
dataset['Embarked'] = dataset['Embarked'].astype(str)
if one_hot:
# 因为OneHotEncoder只能编码数值型,所以此处使用LabelBinarizer进行独热编码
Embarked_arr = LabelBinarizer().fit_transform(dataset['Embarked'])
dataset['Embarked_0'] = Embarked_arr[:, 0]
dataset['Embarked_1'] = Embarked_arr[:, 1]
dataset['Embarked_2'] = Embarked_arr[:, 2]
dataset.drop('Embarked',axis=1,inplace=True)
else:
# 字符串映射处理
dataset['Embarked'] = dataset['Embarked'].map(Passenger_Embarked).astype(int)
# Name选取称呼Title_name
dataset['TitleName'] = dataset['Name'].apply(get_title_name)
dataset['TitleName'] = dataset['TitleName'].replace('Mme', 'Mrs')
dataset['TitleName'] = dataset['TitleName'].replace('Mlle', 'Miss')
dataset['TitleName'] = dataset['TitleName'].replace('Ms', 'Miss')
dataset['TitleName'] = dataset['TitleName'].replace(['Lady', 'Countess', 'Capt', 'Col', \
'Don', 'Dr', 'Major', 'Rev', 'Sir', 'Jonkheer', 'Dona'],
'Other')
dataset['TitleName'] = dataset['TitleName'].map(Passenger_TitleName).astype(int)
# age —— 缺失值,分段处理
if age_default_avg:
# 缺失值使用avg处理
age_avg = dataset['Age'].mean()
age_std = dataset['Age'].std()
age_null_count = dataset['Age'].isnull().sum()
age_default_list = np.random.randint(low=age_avg - age_std, high=age_avg + age_std, size=age_null_count)
dataset.loc[np.isnan(dataset['Age']), 'Age'] = age_default_list
dataset['Age'] = dataset['Age'].astype(int)
else:
# 将age作为label,预测缺失的age
# 特征为 TitleName,Sex,pclass,SibSP,Parch,IsAlone,CategoricalFare,FamileSize,Embarked
feature_list = ['TitleName', 'Sex', 'Pclass', 'SibSp', 'Parch', 'IsAlone','CategoricalFare',
'FamilySize', 'Embarked','Age']
if one_hot:
feature_list.append('Embarked_0')
feature_list.append('Embarked_1')
feature_list.append('Embarked_2')
feature_list.remove('Embarked')
Age_data = dataset.loc[:,feature_list]
un_Age_mask = np.isnan(Age_data['Age'])
Age_train = Age_data[~un_Age_mask] #要训练的Age
# print(Age_train.shape)
feature_list.remove('Age')
rf0 = RandomForestRegressor(n_estimators=60,oob_score=True,min_samples_split=10,min_samples_leaf=2,
max_depth=7,random_state=10)
rf0.fit(Age_train[feature_list],Age_train['Age'])
def set_default_age(age):
if np.isnan(age['Age']):
# print(age['PassengerId'])
# print age.loc[feature_list]
data_x = np.array(age.loc[feature_list]).reshape(1,-1)
# print data_x
age_v = round(rf0.predict(data_x))
# print('pred:',age_v)
# age['Age'] = age_v
return age_v
# print age
return age['Age']
dataset['Age'] = dataset.apply(set_default_age, axis=1)
# print(dataset.tail())
#
# data_age_no_full = dataset[dataset['Age'].]
# pd.cut与pd.qcut的区别,前者是根据取值范围来均匀划分,
# 后者是根据取值范围的各个取值的频率来换分,划分后的某个区间的频率数相同
# print(dataset.tail())
dataset['CategoricalAge'] = pd.cut(dataset['Age'], 5,labels=[0,1,2,3,4])
return full_data
##特征选择
def data_feature_select(full_data):
"""
:param full_data:全部数据集
:return:
"""
for data_set in full_data:
drop_list = ['PassengerId','Name','Age','Fare','Ticket','Cabin']
data_set.drop(drop_list,axis=1,inplace=True)
train_y = np.array(full_data[0]['Survived'])
train = full_data[0].drop('Survived',axis=1,inplace=False)
# print(train.head())
train_X = np.array(train)
test_X = np.array(full_data[1])
return train_X,train_y,test_X
4.2XGBoost参数介绍
要熟练的使用XGBoost库一方面需要对XGBoost原理的了解,另一方面需要对XGBoost库的API参数的了解。此处参考了别人的博客。
4.2.1通用参数
booster,基分类器的模型gbtree和gbliner
nthread,线程数
4.2.2booster参数(gbtree提升树对应的参数)
learning_rate,梯度下降的学习率,一般为0.01~0.2
min_child_weight,最小叶子节点样本权重和,用于避免过拟合,一般为1
max_depth,决策树的最大深度,默认为6
max_leaf_nodes,树上最大的叶子数量
gamma,节点分裂时候和损失函数变化相关,具体可参考XGBoost中决策树节点分裂时的代价函数的公式
subsample和colsample_bytree,随机森林中的两种随机,也是XGBoost中的trick,用于防止过拟合,值为0.5~1,随机采样所占比例,随机列采样比例。
lambda,L2正则化项,可调参实现。
scale_pos_weight,在各类别样本十分不平衡时,把这个参数设定为一个正值,可以使算法更快收敛。
4.2.3学习目标函数
objective,指定分类回归问题。如binary:logistic
eval_metric,评价指标
seeds随机数种子,调整参数时,随机取同样的样本集。
4.3XGBoost调参
主要是五个步骤,按照参数的重要性依次调整。
step1 确定学习速率和迭代次数n_estimators,即集分类器的数量
setp2 调试的参数是min_child_weight以及max_depth
step3 gamma参数调优
step4 调整subsample 和 colsample_bytree 参数
step5 正则化参数调优
def xgboost_change_param(train_X,train_y):
# Xgboost 调参
# step1 确定学习速率和迭代次数n_estimators,即集分类器的数量
xgb1 = XGBClassifier(learning_rate=0.1,
booster='gbtree',
n_estimators=300,
max_depth=4,
min_child_weight=1,
gamma=0,
subsample=0.8,
colsample_bytree=0.8,
objective='binary:logistic',
nthread=2,
scale_pos_weight=1,
seed=10
)
#最佳 n_estimators = 59 ,learning_rate=0.1
modelfit(xgb1,train_X,train_y,early_stopping_rounds=45)
# setp2 调试的参数是min_child_weight以及max_depth
param_test1 = {
'max_depth': range(3,8,1),
'min_child_weight':range(1,6,2)
}
gsearch1 = GridSearchCV(estimator=XGBClassifier(learning_rate=0.1,n_estimators=59,
max_depth=4,min_child_weight=1,gamma=0,
subsample=0.8,colsample_bytree=0.8,
objective='binary:logistic',nthread=2,
scale_pos_weight=1,seed=10
),
param_grid=param_test1,
scoring='roc_auc',n_jobs=1,cv=5)
gsearch1.fit(train_X,train_y)
print gsearch1.best_params_,gsearch1.best_score_
# 最佳 max_depth = 7 ,min_child_weight=3
# modelfit(gsearch1.best_estimator_) 最佳模型为:gsearch1.best_estimator_
# step3 gamma参数调优
param_test2 = {
'gamma': [i/10.0 for i in range(0,5)]
}
gsearch2 = GridSearchCV(estimator=XGBClassifier(learning_rate=0.1,n_estimators=59,
max_depth=7,min_child_weight=3,gamma=0,
subsample=0.8,colsample_bytree=0.8,
objective='binary:logistic',nthread=2,
scale_pos_weight=1,seed=10),
param_grid=param_test2,
scoring='roc_auc',
cv=5
)
gsearch2.fit(train_X, train_y)
print gsearch2.best_params_, gsearch2.best_score_
# 最佳 gamma=0.3
# modelfit(gsearch2.best_estimator_)
#step4 调整subsample 和 colsample_bytree 参数
param_test3 = {
'subsample': [i / 10.0 for i in range(6, 10)],
'colsample_bytree': [i / 10.0 for i in range(6, 10)]
}
gsearch3 = GridSearchCV(estimator=XGBClassifier(learning_rate=0.1,n_estimators=59,
max_depth=7,min_child_weight=3,gamma=0.3,
subsample=0.8,colsample_bytree=0.8,
objective='binary:logistic',nthread=2,
scale_pos_weight=1,seed=10),
param_grid=param_test3,
scoring='roc_auc',
cv=5
)
gsearch3.fit(train_X, train_y)
print gsearch3.best_params_, gsearch3.best_score_
# 最佳'subsample': 0.8, 'colsample_bytree': 0.6
# step5 正则化参数调优
4.4XGBoost训练
待XGBoost调参结束后选择合适的参数,训练模型。
train = pd.read_csv(train_file)
test = pd.read_csv(test_file)
test_y = pd.read_csv(test_result_file)
full_data = [train,test]
# train.apply(axis=0)
full_data = data_feature_engineering(full_data,age_default_avg=True,one_hot=False)
train_X, train_y, test_X = data_feature_select(full_data)
# XGBoost调参
# xgboost_change_param(train_X,train_y)
xgb1 = XGBClassifier(learning_rate=0.1,n_estimators=59,
max_depth=7,min_child_weight=3,
gamma=0.3,subsample=0.8,
colsample_bytree=0.6,objective='binary:logistic',
nthread=2,scale_pos_weight=1,seed=10)
xgb1.fit(train_X,train_y)
y_test_pre = xgb1.predict(test_X)
y_test_true = np.array(test_y['Survived'])
print ("the xgboost model Accuracy : %.4g" % metrics.accuracy_score(y_pred=y_test_pre, y_true=y_test_true))
5实践总结
1.离散型特征进行one-hot编码的要求,OneHotEncoder只能对数值型特征进行独热编码,对字符型特征可以使用LabelBinarizer。
2.Pandas中的apply函数是作用在(axis=1)行Series上的,(axis==0)列Series上的。apply中的func需要返回值,并且return的值重新组合成一个Series作为最后的apply函数的返回。
3.字符型特征处理,有两种处理方式,第一种,直接映射到数值上,第二种进行独热编码LabelBinarizer。
4.缺失值处理,当某个属性列的值缺失极多,则可考虑放弃该列,如果部分缺失,可以使用该列统计的信息如平均值,中位数等进行填充,或者可以采用利用其它列作为特征,没有缺失的数作为label训练模型来预测缺失值的label。如果该属性列缺失极少的话,可以采用取值最多的数进行填充。
6参考链接
Titanic数据集的特征选择
机器学习系列(12)_XGBoost参数调优完全指南