数据结构之通用树结构的实现
之前我们讲了树的定义和操作,这节我们讲一下如何实现这些操作。既然要考虑如何实现,那就得说说树的存储结构。
大家都知道树是非线性数据结构,显然我们无法用数组来表示树的逻辑结构。那我们应该怎么办呢?通过什么来表示呢?其实可
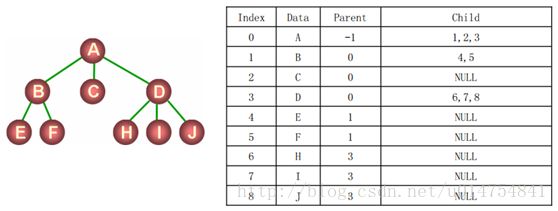
以设计结构体数组对结点间的关系进行表述。如下图所示:
从上图发现,将根结点的双亲定义为-1,表示其没有双亲;将根的孩子结点的双亲定义为0,表示其双亲是根结点;将根结点孩
子1的孩子结点的双亲定义为1,表示其双亲是根结点的孩子结点1;还有双亲定义为根结点孩子3,以此类推就会有4、5、6、7...
等等双亲。通过Child来存放其孩子结点的在结构体数组中下标,这样根据双亲Parent和孩子结点Child就能轻松的访问树结构里
所有元素了。
接下来我们考虑两个现实的问题:1.树结构需要添加删除结点,数组存储是否足够灵活?2.每个结点的子结点可以有多个,如何
存储?到此是不是感觉到很头疼呢?既然要实现树结构的操作,当然希望是一个通用的树结构的操作,可以任意插入结点、删除
结点等。那我们到底应该怎么办呢?
大家都知道,之前我们学习线性表时说过,链表是可以无限扩展,任意插入的,不限长度的,这里我们是否可以也用链表代替这
个结构数组呢?
Of course!我们当然可以利用链表组织树中的各个结点,链表中的前后关系不代表结点间的逻辑关系,结点的逻辑关系由child数
据域描述,child数据域保存其他结点的存储地址。既然提到链表,来我们这里就得复用之前已经实现的链表代码,参考线性表之
单链表。
这里我们的定义两个结构体,链表结点结构体和树结点结构体。如下图:
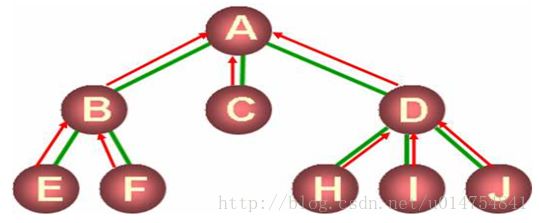
树中每一个结点包含一个指向父结点的指针(如下图红色箭头所示)。
树中每一个结点都是同一个链表中的数据元素,根结点是链表的首元素,根结点的孩子结点从左往右分别是链表的第二个、第三
个。。。等元素,根结点的孩子结点的孩子结点紧跟在链表后面。但是要注意:树结点在链表中的位置不代表树的任何逻辑关
系。
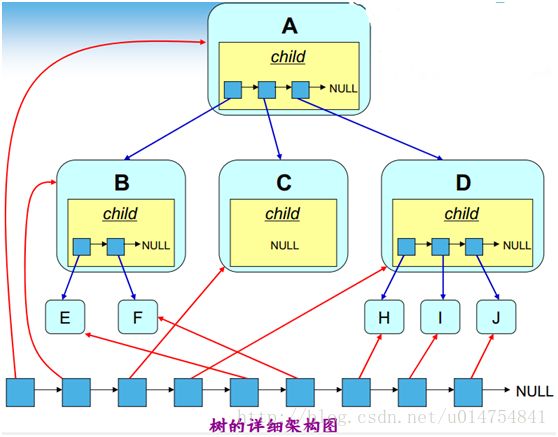
下面我们来看一下树的详细架构图:
由上图我们发现要实现树结构的操作,势必需要两个链表,一个用于记录树所有元素,我们这里称为组织链表、另一个是孩子链
表用来描述树结构的逻辑关系。
说了这么多,我们接下来一步一步的来实现上一节描述的那些操作。
1.创建树
// 创建树
GTree* GTree_Create()
{
return LinkList_Create(); // 调用链表创建函数,定义一个空组织链表,并返回
}这里没啥好说的,不明白的小伙伴可以参考之前的章节。
2.销毁树和清空树
// 销毁树
void GTree_Destroy(GTree* tree)
{
GTree_Clear(tree);
LinkList_Destroy(tree);
}
// 清空树
void GTree_Clear(GTree* tree)
{
GTree_Delete(tree, 0);
}销毁树就是将所有的树结构清空,并且释放所有申请内存,代表着这个东西不存在了,清空树就是将树变成空树,也就是将其从
根结点删除。
3.插入数据
根据结构图我们知道,树中的一个元素不仅要在组织链表中,还要在其组织链表的孩子链表中,这就需要申明两个链表结点结构
体内存来用于插入链表(比如结构图中的成员B不仅在组织链表中,而且还包含在A成员的孩子链表中),实现方法如下:
首先定义插入所需要的树结点结构体变量,用于处理插入元素,接着进行入口参数合法性检查,如果不合法,直接返回NULL;
如果合法,开始插入元素:
1.定义存放树结点、孩子结点和插入元素结点结构体变量,并且分别为其定义的结构体申请内存,同时获取当前插入位置双亲的
元素地址;
2.对申请内存合法性进行检查;
2.1.内存申请成功:
2.1.1.处理插入元素,保存插入元素数据、初始化插入元素双亲(默认为NULL,无双亲)、创建孩子结点链表;
2.1.2.将树结点和孩子结点地址指向插入元素结点地址,并在树结点链表(组织链表)尾部插入树结点元素;
2.1.3.检查一下插入位置是否合法,合法,将插入元素的双亲指向当前元素(双亲)的结点地址,在树孩子结点链表(孩子
链表)尾部插入孩子结点元素,否则,释放申请的孩子结点内存,退出插入操作;
2.2.内存申请失败,释放内存,退出插入操作;
实现代码如下:
// 在树结构指定的位置pPos插入元素data
// pPos:要插入元素的双亲的位置,即在那个双亲下插入
int GTree_Insert(GTree* tree, GTreeData* data, int pPos)
{
// 定义链表结点结构体
LinkList* list = (LinkList*)tree;
// 定义返回变量,并且检查参数合法性
int ret = (list != NULL) && (data != NULL) && (pPos < LinkList_Length(list));
// 合法性OK
if( ret )
{
TLNode* trNode = (TLNode*)malloc(sizeof(TLNode)); // 定义链表结点结构体,并申请内存,存放树结点链表成员
TLNode* cldNode = (TLNode*)malloc(sizeof(TLNode)); // 定义链表结点结构体,并申请内存,存放孩子结点链表成员
TLNode* pNode = (TLNode*)LinkList_Get(list, pPos); // 定义链表结点结构体,保存pPos位置的元素
GTreeNode* cNode = (GTreeNode*)malloc(sizeof(GTreeNode)); // 定义树结点结构体,并申请内存,存放要插入元素内容
// 内存申请合法性检查
ret = (trNode != NULL) && (cldNode != NULL) && (cNode != NULL);
// 内存申请成功
if( ret )
{
cNode->data = data; // 保存要插入的元素地址
cNode->parent = NULL; // 双亲地址指向NULL
cNode->child = LinkList_Create(); // 创建孩子链表
trNode->node = cNode; // 树结点指向要插入元素结点地址
cldNode->node = cNode; // 树孩子结点指向要插入元素结点地址
// 在树结点链表(组织链表)尾部插入树结点元素
LinkList_Insert(list, (LinkListNode*)trNode, LinkList_Length(list));
// 要插入的位置合法,不是根结点
if( pNode != NULL )
{
cNode->parent = pNode->node; // 将要插入元素的双亲指向当前元素的结点地址
// 在树孩子结点链表(孩子链表)尾部插入孩子结点元素
LinkList_Insert(pNode->node->child, (LinkListNode*)cldNode, LinkList_Length(pNode->node->child));
}
else
{
free(cldNode);
}
}
// 内存申请不成功,释放内存
else
{
free(trNode);
free(cldNode);
free(cNode);
}
}
return ret;
}4.打印树结构
上面我们讲解了树结构插入的操作,但是因为树结构是非线性的,所有我们也不知道是否操作的正确,就算查看地址也因为非线
性不连续的而行不通,所以我们应该写一个显示函数,可以将插入树结构的数据按照层次(自定义格式)打印出来。
树结构的显示,归根结底就是遍历树成员,将其打印出来。由于树的定义是非线性、采用递归的形式的,所以树结构的显示必然
也需要递归来实现。实现的思路如下:
首先先打印根结点,然后遍历根结点的孩子结点,遍历的过程中打印孩子结点,打印孩子结点时就会遍历该孩子结点的孩子结
点,直至遍历结束,所需的树结构也就打印出来了。
实现代码如下:
// 按指定格式显示树结构,使用文本形式,缩放的方式
// pFunc 显示方式式函数的地址
// 孩子结点显示空格增量
// 孩子结点显示格式'-'
/* eg:pFunc:%c gap = 2 div = '-'
A
--B
----E
----F
--C
--D
----H
----I
----J
*/
void GTree_Display(GTree* tree, GTree_Printf* pFunc, int gap, char div)
{
// 定义树结点结构体,用于存放获取的根结点成员,即组织链表的首元素
TLNode* trNode = (TLNode*)LinkList_Get(tree, 0);
// 获取根结构成员成功,入口参数合法,调用显示递归函数
if( (trNode != NULL) && (pFunc != NULL) )
{
recursive_display(trNode->node, pFunc, 0, gap, div);
}
}
显然,我们递归时直接调用GTree_Display()函数是实现不了打印树结构的,所以我们单独定义了一个实现递归函数。实现代码
如下:
// 显示树结构递归函数
static void recursive_display(GTreeNode* node, GTree_Printf* pFunc, int format, int gap, char div)
{
int i = 0;
// 合法性检查
if( (node != NULL) && (pFunc != NULL) )
{
// 循环打印缩进格式
for(i=0; idata);
// 空行
printf("\n");
// 遍历孩子链表,打印孩子链表成员数据
for(i=0; ichild); i++)
{
// 获取每一个链表元素,用于递归打印
TLNode* trNode = (TLNode*)LinkList_Get(node->child, i);
// 调用递归函数,按格式打印孩子结点数据
recursive_display(trNode->node, pFunc, format + gap, gap, div);
}
}
} 遍历孩子结点时调用显示递归函数,这里还有一个pFunc可能大家感到迷茫,莫名其妙,其实这是自定义的一个函数类型,用于
定义打印内容的格式(字符、字符串、整数等),代码如下:
typedef void (GTree_Printf)(GTreeData*);
void printf_data(GTreeData* data)
{
printf("%c", (int)data);
}打印的结果如下图:
5.删除结点
通过上面插入结点的操作,我们知道树结构的插入分两步,第一步往组织链表里插入结点、第二步向孩子链表中插入结点,所以
树结构是链表中嵌套着链表分层次、不确定元素个数和要删除结点的性质的(可能是分支结点、也可能是叶结点,还有可能直接
就是根结点)。如果是分子节点,那么它的孩子结点可能还不止一个,同时还可能有子孙结点,所以我们就得依次一个一个、一
层一层的删除,确保要删除结点、其孩子结点和子孙结点全部被删除。也就是说删除也要分两步,首先删除组织链表里的结点,
再将组织链表里结点的孩子结点也要删除,然后用上递归的思想继续删除子孙结点,直至删除完毕为止。实现方法如下:
首先要从组织链表中找到要删除的结点地址,然后保存要删除的结点数据,最后调用删除递归函数。实现代码如下:
// 删除树结构指定位置pos的元素
GTreeData* GTree_Delete(GTree* tree, int pos)
{
// 定义树结点结构体变量,获取要删除结点当前位置的元素地址
TLNode* trNode = (TLNode*)LinkList_Get(tree, pos);
// 定义返回变量
GTreeData* ret = NULL;
// 要删除结点的位置元素合法
if( trNode != NULL )
{
ret = trNode->node->data; // 保存当前位置元素数据地址,用于函数返回
recursive_delete(tree, trNode->node); // 调用递归,删除结点
}
return ret;
}递归删除函数实现方法如下:
1.合法性检查;
2.找到要删除结点的双亲指针;
3.从组织链表中删除结点;
3.1.遍历链表,寻找要删除的结点;
3.1.1.找到后就删除该结点;
3.1.2.释放该结点内存;
3.1.3.标记已经找到删除结点,并跳出遍历链表操作;
3.2.找不到要删除的元素直接进行后面的操作;
4.从孩子链表中删除孩子结点及其子孙结点;
4.1.遍历链表,寻找要删除的结点;
4.1.1.找到后就删除该结点;
4.1.2.释放该结点内存;
4.1.3.标记已经找到删除结点,并跳出遍历链表操作;
4.2.找不到要删除的元素直接进行后面的操作;
5.如果存在子孙结点,调用递归函数删除所有的子孙结点。
实现代码如下:
// 结点删除递归函数
// list:要删除的树结构
// node:要删除的结点
static void recursive_delete(LinkList* list, GTreeNode* node)
{
// 入口参数合法性检查OK
if( (list != NULL) && (node != NULL) )
{
// 定义一个树结点结构体变量,存放要删除位置的双亲地址
GTreeNode* parent = node->parent;
int index = -1; // 查找变量
int i = 0; // 循环变量
// 遍历树结构组织链表,找到要删除结点的位置
for(i=0; inode == node )
{
LinkList_Delete(list, i); // 删除该位置的树结构成员
free(trNode); // 释放内存,防止内存泄漏
index = i; // 标记要删除结点在组织链表中的位置
break; // 跳出遍历树结构操作
}
}
// 删除位置真实存在
if( index >= 0 )
{
// 有双亲
if( parent != NULL )
{
// 遍历孩子结点链表,将其从双亲的孩子结点中删除
for(i=0; ichild); i++)
{
// 定义结点链表结构体变量,存放遍历的双亲的孩子结点链表成员
TLNode* trNode = (TLNode*)LinkList_Get(parent->child, i);
// 找到要删除的孩子结点
if( trNode->node == node )
{
// 将其从双亲的孩子链表中删除
LinkList_Delete(parent->child, i);
// 释放内存,防止内存泄漏
free(trNode);
// 跳出遍历孩子结点链表操作
break;
}
}
}
// 如果存在子孙结点,递归删除其他结点
while( LinkList_Length(node->child) > 0 )
{
// 获取子孙结点链表首元素
TLNode* trNode = (TLNode*)LinkList_Get(node->child, 0);
// 调用递归函数,继续删除
recursive_delete(list, trNode->node);
}
// 销毁子孙结点链表
LinkList_Destroy(node->child);
// 释放内存,防止内存泄漏
free(node);
}
}
} 6.获取指定的结点
实现代码如下:
// 获取树结构指定位置pos的元素
GTreeData* GTree_Get(GTree* tree, int pos)
{
// 定义树结点结构体变量,存放要获取结点当前位置的元素地址
TLNode* trNode = (TLNode*)LinkList_Get(tree, pos);
GTreeData* ret = NULL;
// 要获取的结点的位置元素合法,返回该结点成员数据
if( trNode != NULL )
{
ret = trNode->node->data;
}
return ret;
}从上面代码上可以发现,获取结点有点类似删除结点,就是少了删除的操作。
7.获取根结点
获取根结点其实就是获取树结构的首元素,实现代码如下:
// 获取树结构的根结点元素
GTreeData* GTree_Root(GTree* tree)
{
return GTree_Get(tree, 0); // 调用获取树结点函数
}8.获取树结构的高度
获取树结构的高度,我们可以这样考虑,先求出根结点的子结点的高度,然后找到最大值后再加上1不就是整个树的高度了;但
是有一个问题就是,子结点还会有子结点,那怎么办呢?好办呀,按照如上的方法、利用递归的思想,一层层的求子结点的高
度,最后返回的结果就是整个树的高度了,实现代码如下:
// 获取树结构的高度
int GTree_Height(GTree* tree)
{
// 定义树结点结构体变量,存放子树结点
TLNode* trNode = (TLNode*)LinkList_Get(tree, 0);
int ret = 0;
// 根结点合法,调用获取树结构高度递归函数,返回高度
if( trNode != NULL )
{
ret = recursive_height(trNode->node);
}
return ret;
}递归函数实现代码如下:
// 获取树结构高度递归函数
static int recursive_height(GTreeNode* node)
{
int ret = 0;
// 结点合法
if( node != NULL )
{
int subHeight = 0; // 子结点
int i = 0; // 循环变量
// 遍历子树的孩子结点链表
for(i=0; ichild); i++)
{
// 依次取出子树结点的孩子结点
TLNode* trNode = (TLNode*)LinkList_Get(node->child, i);
// 调用求高度递归函数,计算子结点
subHeight = recursive_height(trNode->node);
// 求计算结果的最大值,边计算边找最大值
if( ret < subHeight )
{
ret = subHeight;
}
}
// 计算结果加1就是整个树的高度
ret = ret + 1;
}
return ret;
} 9.获取树结构的全体成员数量
获取树结构的全体成员数量也就是获取整个组织链表的长度,实现代码如下:
// 获取树结构的元素数量
int GTree_Count(GTree* tree)
{
return LinkList_Length(tree);
}10.获取树结构的度
获取树结构的度的实现方法和获取树结构的高度的实现思想差不多,也是先将根结点的度求出来,然后找求根结点所有子树结点
的度,然后找出最大值,就是树的度数了,还是要利用递归的思想。实现代码如下:
// 获取树结构的度
int GTree_Degree(GTree* tree)
{
// 定义树结点结构体变量,存放子树结点
TLNode* trNode = (TLNode*)LinkList_Get(tree, 0);
int ret = -1;
// 根结点合法,调用获取树结构度递归函数,返回高度
if( trNode != NULL )
{
ret = recursive_degree(trNode->node);
}
return ret;
}递归函数代码实现如下:
// 获取树结构度递归函数
static int recursive_degree(GTreeNode* node)
{
int ret = -1;
// 结点合法
if( node != NULL )
{
int subDegree = 0; // 子结点度
int i = 0;
// 获取子结点的长度,即度
ret = LinkList_Length(node->child);
// 变量子树孩子结点的成员
for(i=0; ichild); i++)
{
// 依次取出子树结点的孩子结点
TLNode* trNode = (TLNode*)LinkList_Get(node->child, i);
// 调用求度递归函数,计算子结点度
subDegree = recursive_degree(trNode->node);
// 求计算结果的最大值
if( ret < subDegree )
{
ret = subDegree;
}
}
}
return ret;
} 本节中的树结构是一种通用的数据结构。
利用链表组织树结点优点:能够便利的存取结点。
利用链表组织树结点缺点:链表的维护具有一定复杂性。
树结构的非线性特性和递归定义的特性是树结构实现难度较大的根本原因。
至此,有关树结构的基本操作已经实现了,因是初学,有描述不妥的地方还清大神加以指正。
通用树结构C代码实现