OpenGL学习笔记与水面波纹实例

一、OpenGL

1.简介

简单来说，OpenGL是一个图形程序的接口，可用于图形程序开发和游戏开发。如果你是使用C／C++语言编写有关图像界面、图像操作的程序，使用OpenGL是一个不错的选择。

2.环境配置

使用OpenGL，需要配置相关的环境。这里我列出有关mac os下是如何进行OpenGL的环境配置，至于其他系统下的配置方法，我将在本文末附上一个链接，大家可以参考之。
对于Mac，OpenGL的环境配置十分简单，这是因为XCode上已经有相关的包，我们只需要在对应的project加把这些包添加进去即可。具体步骤如下：
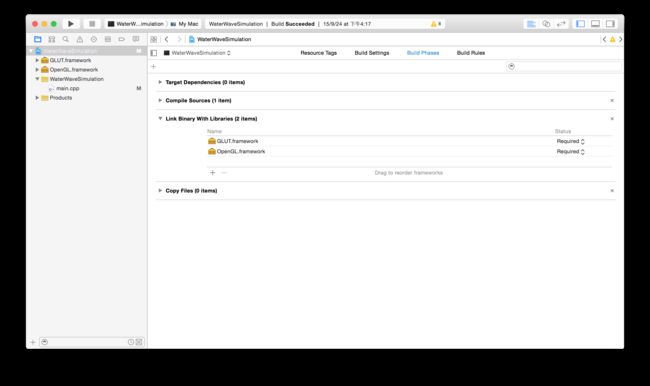
1）创建好project之后，在Xcode左侧项目导航区点击我们创建的project（注意是点击项目，而不是点击项目下的子目录文件），将在中间出现一个新界面；
2）点击界面中的“Bulid Phases”；
3）点击“Link Binary With Libraries”；
4）点击“＋”，找到“GLUT.framework”、“OpenGL.framework”这两个包，添加即可。

附上截图：

以上就是mac上配置OpenGL的方法，相比其他系统是相当简单的。

这里有两点需要额外提出：

1）我使用的版本为XCode 7，其他版本的相关界面、操作可能有所区别，但关键就是找到“Bulid Phases”这个选项；
2）由于XCode其实是用来写Object－C的，虽然也可以写C++，但是有可能在写C++的时候会出现一些奇奇怪怪的问题。在实现水面波纹绘制的编程过程，我就遇到一个神奇的问题，在这里拿出来跟大家分享一下。

问题：

代码编写好后build and run， 能够成功build，但是run就没反应，在程序某处会自动被打上断点，可执行程序一直是未响应；但是如果我在成功build完后直接去到可执行文件的目录下手动打开，却是可以执行。

解决：

将.cpp文件的后缀改成.m后，问题解决。
（具体的原理和问题所在我也不太清楚，）

3.OpenGL函数

这里我分享一下OpenGL的函数的一些特色，了解这些特色后，看这些函数就会容易很多。我将OpenGL的函数名分成五部分，分别是：库类型、函数功能、维数、参数类型、向量标记。
以glVertex2fv为例：
1）gl：指的是所用的库类型。OpenGL中有基础库、实用库、实用工具库、辅助库、X窗口扩充库，其前缀分别是：gl、glu、glut、aux、glux。其中，gl提供了最基本的3D函数，glu是对gl的补充，而glut是对应于glu和gl的，是一个跨平台的图形窗口界面。
2）Vertex：表明函数的功能与点(vertex)有关，其实就是画出给定坐标的点，不过需要配合glBegin、glEnd使用。再举一例：glRotated，由Rotated很容易知道此函数用于旋转变换。
3）2:指的是维数，在本函数中表明画出的点的坐标是二维坐标。注意有些函数是没有的，如glRotated。
4）f：指的是参数的数据类型为浮点型，如果是d的话就指的是double的类型，i同理。同样，请注意有些函数是没有的。
5）v：表明该函数参数可以由一个向量（数组）给出。如，我可以给glVertex2f传入｛2.0，3.0｝定义出一个坐标为（2.0，3.0）的点。同上，请注意有些函数是没有的。

4.OpenGL设计框架

此框架是对于编写一个简单的图形程序而言，分别是定义一个窗口、清屏操作、在窗口中展示内容、窗口大小的重定义以及事件的无限循环。如下图所示：

0）初始化glut库。使用glutInit函数，该函数接受来自main函数的参数，应在其他OpenGl函数、glut函数之前调用
1）定义窗口。包括定义初始窗口模式、窗口大小位置、创建一个窗口等。
2）清屏。使用的函数是glClearColor和glColor3f，将窗口清为黑色。
3）在窗口中展示内容。使用glutDisplayFunc，传入自定义的display函数。
4）窗口大小的重定义。使用glutReshapeFunc，传入自定义的reshape函数。可以使拉伸窗口时，投影区域随之增大缩小，动态改变点的显示范围，与之相关的函数是glOrtho。
5）事件的无限循环。使用glMainLoop，让与事件有关的函数无限循环，进行不断的刷新。

代码如下：

int main(int argc, char ** argv) {
    glutInit(&argc, argv);
    glutInitDisplayMode(GLUT_SINGLE|GLUT_RGBA);
    glutInitWindowSize(640, 480);
    glutInitWindowPosition(100, 100);
    glutCreateWindow("WaterWaveSimulation");
    init();
    glutDisplayFunc(display);
    glutReshapeFunc(reshape);
    glutMainLoop();
    return 0;
}

二、水面波纹实例

1、实验思路

1）主体思路

对OpenGL程序框架中的glutDisplayFunc方法传入自定义的函数display，在该函数中实现水面波纹的仿真。

2）细节实现

关于水面波纹的实现，主要就是利用傅立叶原理——自然界中任何一种波可以由若干不同角频率的正余弦函数叠加而来。通过不同正余弦函数的组合，就可以模拟出比较接近真实的水面波纹了。但是，这样还只停留在二维，还需要将其扩展到三维，成为真正的一个面。在这里，我想到到两种方法。
一是利用贝塞尔曲面，先得出可以反映曲面起伏若干点，然后将其视作控制点画出一个贝塞尔曲面；第二种方法是将二维中的仿真波纹函数的每一个旋转360度，旋转的过程记下运动轨迹。
这两种想法我都有实现，而且结果各异，至于具体情况，将在实验过程设计中阐述。

2、实验过程设计

1）基本设计

首先是一些窗口环境的初始化设置，如显示模式、窗口位置大小以及创建窗口等，从而定义了一个窗口，这些直接调用OpenGL基础库、实用库函数即可。
然后是一个窗口内清屏，将窗口清为黑色。
对于两种方法的初始化设置，在用贝塞尔曲面的方法中还需要对曲面进行定义、启动以及后续的关闭。

2）核心设计

a）贝塞尔曲面方法：

getWave函数用来获取控制点。首先通过f(x)求出八个点，这八个点需要反映到函数的起伏情况；然后将这八个点分三组赋值给控制点数组，其中x、y坐标分别为这八点的横纵坐标，每一组的z坐标均相同，三组间的z坐标各不相同。在display方法中用glEvalCoord2f方法画出曲面。

b）旋转方法：

getWave函数画出曲面。一共两层循环，第一层循环在xy平面画出一个点，然后在第二层循环内绕y轴旋转360度，每旋转1度把当前点画出。注意，OpenGL中的glRotated只是一个旋转变换，并不能通过这个函数获得三维图像。

3）后续设计

设计窗口形状重定函数，参数指针指向函数reshape，它的两个参数就是窗口的新宽度和新高度。然后用glViewport(0, 0, w, h)重定视口，并且在新视口内重新定义投影矩阵。glutMainLoop()，让与“事件”有关的函数调用无限循环，程序中是让display、reshape无限循环。

3、实验关键代码

1）贝塞尔方法

//曲面的启动与关闭
void myinit(void){
    glClearColor (0.0, 0.0, 0.0, 1.0);
    glMap2f(GL_MAP2_VERTEX_3, 0, 1, 3, 8, 0, 1, 24, 3, &ctrlpoints[0][0][0]);
    glEnable(GL_MAP2_VERTEX_3);
    glMapGrid2f(20, 0.0, 1.0, 20, 0.0, 1.0);
    glEnable(GL_DEPTH_TEST);
}

//控制点的获取
GLfloat v[8][3];
GLfloat ctrlpoints[3][8][3];

void getWave() {

    float x=0;
    int m = 0;

    for(;x<4.0;x+=0.5) {
        double func = exp(-x) * cos(2*3.14159265*x);
        //GLdouble func = sin(x*2);
        //glVertex2d(A*x+B,C*func+D);
        //glVertex3d(x, func, 0.0);
        v[m][0] = 1.6*x;
        v[m][1] = 2.4*func;
        v[m][2] = 0;
        m++;
    }
    int i, j, z, zi;
    zi = -2.0;
    for (i = 0; i < 3; i++) {
        for (j = 0; j < 8; j++) {
            for (z = 0; z < 2; z++) {
                ctrlpoints[i][j][z] = v[j][z];
            }
            ctrlpoints[i][j][z] = zi;
        }
        zi += 2.0;
    }
}

//绘制曲面
void CALLBACK display(void){
    int i, j;
    glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
    glColor3f(0.3, 0.6, 0.9);
    glPushMatrix ();
    glRotatef(45.0, 1.0, 1.0, 1.0);

    for (j = 0; j <= 8; j++){
        glBegin(GL_LINE_STRIP);
        for (i = 0; i <= 30; i++)
            glEvalCoord2f((GLfloat)i/30.0, (GLfloat)j/8.0);
        glEnd();
        glBegin(GL_LINE_STRIP);
        for (i = 0; i <= 30; i++)
            glEvalCoord2f((GLfloat)j/8.0, (GLfloat)i/30.0);
        glEnd();
    }
    DrawPoints();
    DrawAxis();
    glPopMatrix ();
    glFlush();
}

2）旋转方法

void getWave() {
    float x = 0;
    glBegin(GL_POINTS);
    for (; x < 4.0; x += 0.005) {
        double y = exp(-x)*cos(2*PI*x);
        glVertex3d(x, y, 0.0);
        int a = 0;
        double xr, zr, z = 0.0;
        for (; a < 360; a += 1) {
            xr = x*cos(a)+z*sin(a);
            zr = z*cos(a)-x*sin(a);
            glVertex3d(xr, y, zr);
        }
    }
    glEnd();
｝

4、实验结果

1）贝塞尔方法

2）旋转方法

附：
参考资料：
OpenGL基础图形编程：
http://blog.chinaunix.net/uid-20638550-id-1909183.html
nehe的OpenGL教程–on mac ：
http://blog.csdn.net/dinko321/article/details/41351725
OpenGL超级宝典笔记——贝塞尔曲线和曲面：
http://m.oschina.net/blog/183721
OpenGL_Qt学习笔记之_03(平面图形的着色和旋转)：
http://www.cnblogs.com/tornadomeet/archive/2012/08/23/2653305.html
OpenGL3.3+教程：
http://www.opengl-tutorial.org/zh-hans/
bezier曲线和bezier曲面：
http://blog.csdn.net/psophia/article/details/6000710