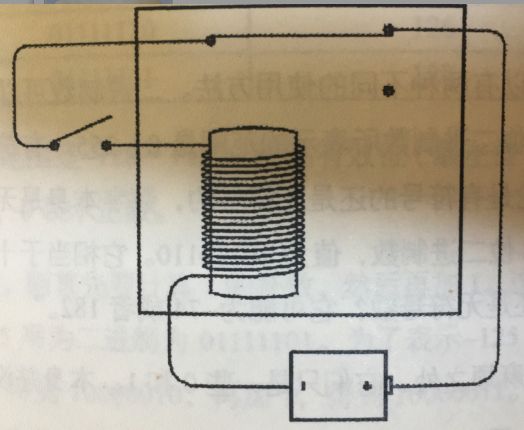
电可以让物体运动,下面我们来看下这么一个器件:
这个器件中,当开关闭合电时候,磁铁线圈通电,磁化。吸引了上面的开关断开,上面的开关断开后,没有了电流,就不能磁化了,然后开关又折回去。以此反复。
这就是蜂鸣器的组成原理。
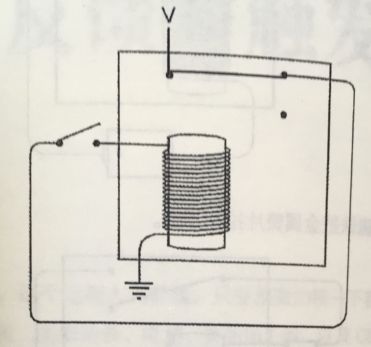
那么如何让我们一直研究的继电器,变成蜂鸣器呢?连接图如下:
原理是一样的,连接方法不同而已。
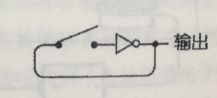
这种图的逻辑是不是跟反向器的逻辑是一样的?电路简化如下:
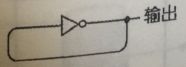
将开关移除,反向器就可以一直反复的工作了:
反向器的输出与输入是相反的,但关键的是,输出同时又是输入。反向器本质上就是一个继电器,而继电器将状态取反得到另外一个状态是需要一点点时间的。
那么电路的输出是什么呢?其实就是要么提供电压,要么不提供电压,在两者之间切换。也就是说,输出结果要么是0,要么是1
这种电路我们称做为震荡器,它不需要人为的干预,完全可以自发的工作。
单片机的晶振工作模式跟这个很类似,在电路组成的自动控制系统中,类似这种振荡器是必须要有的。
一个初始状态一段时间后又回到先前初始状态的这么一个过程,叫做周期。一秒钟的循环次数叫做赫兹(Hz)
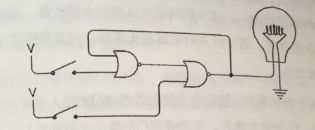
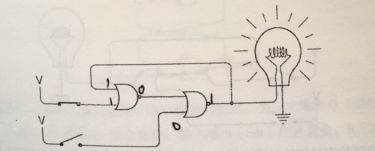
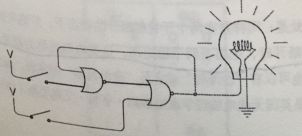
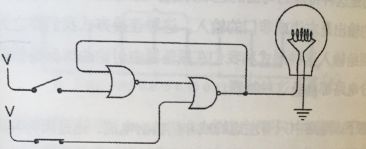
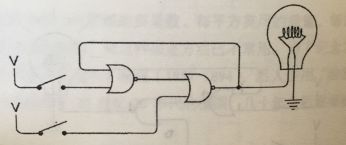
下面我们来看看另外一个电路
左边或非门的输出是右边或非门的输入,而右边或非门的输出是左边或非门的输入。这种连接方式我们称之为 反馈
初始状态下,电路中只有左边的或非门输出电流,这是因为其两个输入均为0.
然后我们闭合上面的开关,左边或非门将立刻输出0,而右边或非门的输出会随之变为1,灯泡将被点亮。
有趣的是,这时你一旦关闭上边的开关,灯泡依然闪闪发光。这时由于左边或非门的输出中有一个为1,所以左边或非门一直输出0,因而左边的或非门输出不便,所以灯泡仍然亮着。
我们现在发现,电路的开关跟初始状态是一样的,只是灯泡居然是亮了。且无论上面的开关怎么变化,灯泡的状态都是不变的。
如果我们闭合下面的开关,灯泡就会熄灭:
再去断开下面开关,灯泡仍旧是不亮。现在这个状态跟初始状态是一样的。
我们将情况总结一下:
1、接通上面的开关,灯泡被点亮,断开此开关,灯泡仍然亮着。
2、接通下面的开关,灯泡被熄灭,断开此开关,灯泡仍然不亮。
当两个开关都断开时,电路有两个稳定状态,这类电路统称为触发器(Flip-Flop)。
触发器电路可以保持信息,它可以“记住”某些信息。对于本章讲的,它可以记住最近一次是哪个开关先闭合:如果灯泡是亮的,你就可以推出最后一次连通的是上面的开关,如果灯泡不亮则可以推测出最后一次连通的是下面的开关。
触发器是一种必不可少的工具,它们可以让电路“记住”之前发生的事情。想象一下,如果你没有了记忆力,该如何去数数,我们不记得刚刚数过的数,当然也就无法确定下一个数是什么。
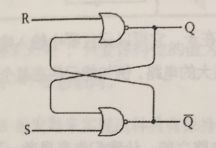
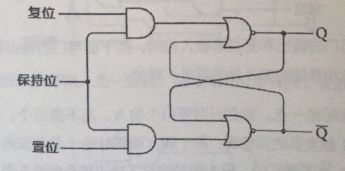
触发器种类繁多,先前所讲述的是最简单的一种R-S(Reset-Set,复位/置位)触发器。我们通常把两个非或门绘制成另一种形式,加上标识符号就得到下面这张图
我们通常用Q来表示用于点亮灯泡的输出状态。另一个Q反是对Q的取反。Q是0,Q反就是1,反之亦然。输入端S(Set)用来置位,R(Reset)用来复位。
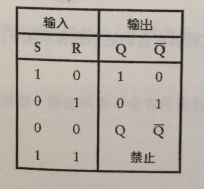
你可以把“置位”理解为把Q设为1,而“复位”是把Q设为0.当状态S为1时(对应先前触发器中上面的开关闭合的情况),此时Q变为1而Q反变为0;当R状态为1时(对应前面图中闭合下面的开关的情况),此时Q变为0而Q反变为1.当S和R均为0时,输出保持Q原来的状态不变。总结的结论如下:
这类表称为功能表、逻辑表或真值表。它表达了不同输入组合所对应的不同输出结果。因为R-S触发器仅有两个输入端,所以不同的输入组合共有4中,分别对应表中的4行。
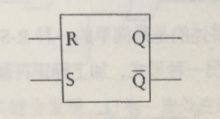
R-S简化图如下
R-S触发器最突出的特点在于,它可以记住哪个输入端的最终状态为1。但是有时候我们需要一种记忆能力更加强大的电路,能记住某个特定时间点上的信号时0还是1.
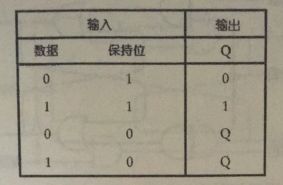
真值表如下:
保持位为1,输入与输出相同,保持位为0的时候,输出端Q与前一个状态保持一致。且不再受输入数据位的影响。
简化如下:
改造R-S,我们需要输入端增加两个与门
复位和置位都需要保持位,否则与门输出都为0.
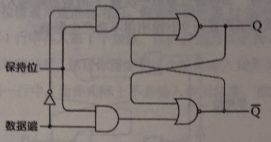
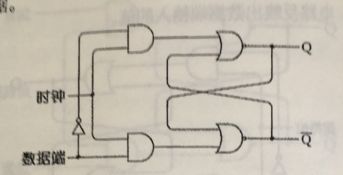
我们只想要两个输入,而不是三个。两个输入端同时为1是非法的,而两个输入端同时为0是无意义的,因为那种情况下,会保持输出不变。所以我们只要将保持位设置为0,就完全可以实现相同的功能。如果把数据端信号看做置位信号,把它取反后的值看做复位端信号,如下图:
这个电路称为电平触发的D型触发器,D(Data)表示数据端输入。所谓的电平触发是指当保持位输入为某一特定电平(本例中为“1”)时,触发器才保存数据端的输入值。
通常情况下,保持位被标记为时钟,当然这种信号不是真正的时钟,但是某些情况下,它却具有类似时钟的属性,即它可以在0和1之间有规律的来回变化。但是现在时钟仅仅用来指示什么时候保存数据。
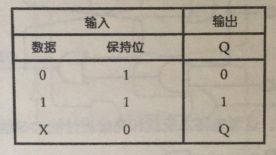
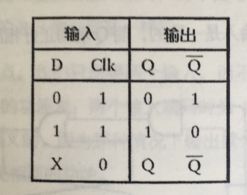
通常把数据端简写为D,时钟端简写为Clk,功能表如下:
这个电路也就是所谓的电平触发的D型锁存器,它表示电路锁存住一位数据并保持它。这个电路也可以被称为1位存储器。
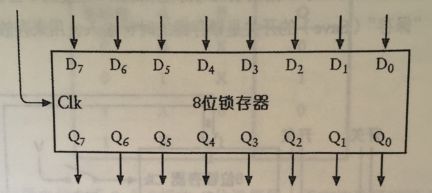
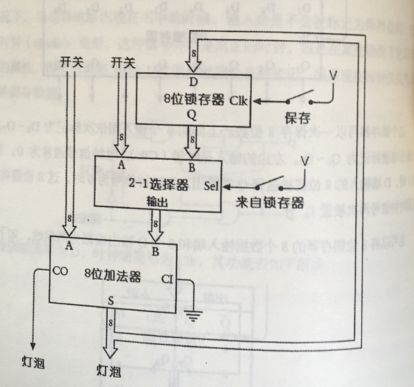
我们在一个小盒子里布置8个锁存器,所有连接如下图:
简化如下:
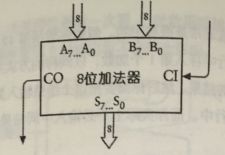
我们先回忆下8位加法器
然后我们组合如下
标记位“保存”的是锁存器的时钟输入,用来存放加法器的运算结果。
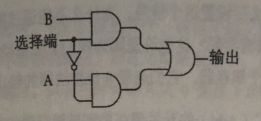
2-1选择器的方块就是让你用一个开关来选择加法器的B端输入是取自第2排开关还是取自锁存器的Q端输出。开关闭合时,就选择了用8位锁存器的输出作为B端输入。2-1选择器使用了8个如下所示的电路:
可以慢慢体会下选择端开关闭合和打开的情况。
改进后的加法器包含了8个这样的1位选择器,所有选择端的输入信号都是连在一起的。
对于加法器来说,一个更好的改进方法是去掉一整排8个开关。但是首先要对D触发器做一些修改,为它加一个或门和一个称为清零(Clear)的输入信号。清零信号通常为0,但当它为1时,Q输出为0,如下图所示:
无论其他信号是什么,清零信号总是强制的使Q输出为0,以达到使触发器清零的目的。
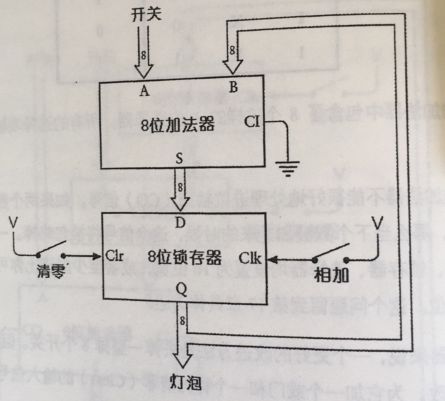
或许你会觉得把时钟端置1,把数据端置0更加方便的清零。因为我们无法精确的控制数据端的输入信息,一组8个锁存器,连接着8位加法器的输出端。
上面这图的设计精妙之处在于可连续运算加法,首先,按下清零开关,清零。A端开关输入第一个加数,然后闭合“相加”开关(时钟),第一个数被保存到8位锁存器中,然后输入第二个数,再次闭合“相加”开关,可以再次相加保存到寄存器上。以此反复。
对于某些应用来说,电平触发时钟输入已经足够用了,但是对另外一些应用来说,边沿触发(edge-triggered)时钟输入则更有效。对于边沿触发器而言,只有当时钟从0跳变到1时,才会引起输出的改变。再时钟输入从0到1的瞬间,数据端的输入才会影响边沿触发器的输出。
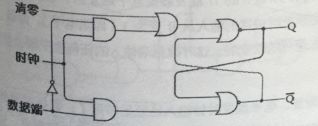
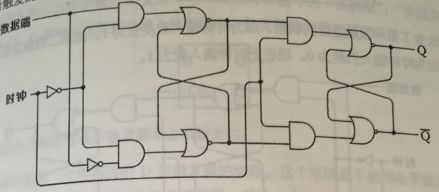
边沿触发的D型触发器是由两级R-S触发器按如下方式连接而成的。
大家可以仔细看看,会发现只有时钟从0变成1的时候,数据端输入才会被保存下来。
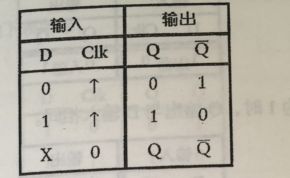
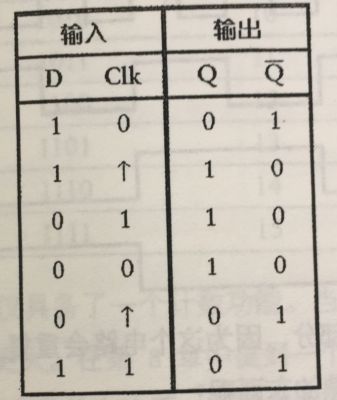
真值表如下:
向上箭头表示从0到1的瞬间变化。也叫做“正跳变”,“负跳变”相反。
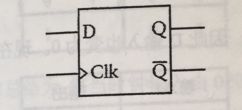
触发器符号如下图:
图中小三角符号表示触发器时边沿触发。
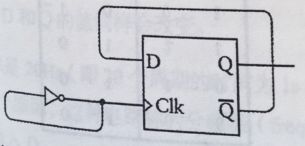
下面我们来看一个示例电路
一个振荡器连接着我们的边沿触发器。触发器的输出同时又是自己的输入,反馈紧接着反馈!(实际上,这种构造可能有问题,其他的继电器不一定能跟得上振荡器的速度。我们假设振荡器中的继电器,比其他电路中的继电器速度要慢得多)变化如下:
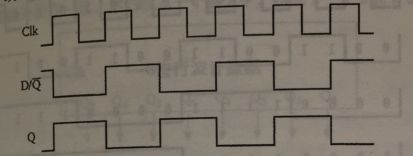
以上发生的现象可以归纳为:每当时钟输入从0变为1时,Q端输出就发生变化,变化从0到1或者从1到0.如下的时序图:
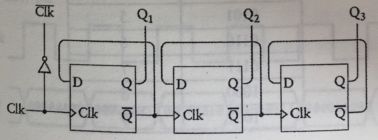
如果这个振荡器的频率时20Hz,那么Q的输出频率是10Hz,由于这个原因,这种电路被称为分频器(frequency divider),它的Q反输出反馈到触发器的数据端输入。也能多个分频器相连,继续分频:
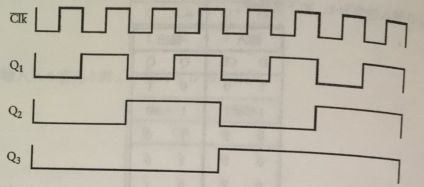
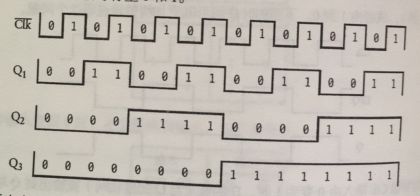
变化规律如下:
我们把这些信号标上0和1:
如果我们垂直来看这些数字,你会发现:
| 二进制 | 十进制 |
| 0000 | 0 |
| 0001 | 1 |
| 0010 | 2 |
| 0011 | 3 |
| 0100 | 4 |
| 0101 | 5 |
| 0110 | 6 |
| 0111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | 10 |
| 1011 | 11 |
| 1100 | 12 |
| 1101 | 13 |
| 1110 | 14 |
| 1111 | 15 |
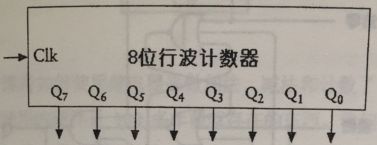
可以看出,这个电路具备了一个计数功能,把八个这样的触发器连在一起,然后放入一个盒子中,构成了一个8位计数器。
这个计数器称为“8位行波计数器”,因为每一个触发器的输出都是下一个触发器的时钟输入。变化再触发器中一级一级的顺序传递,最后一级的触发器变化必定有一些延迟,更先进的计数器是“并行(同步)计数器”,这种哦那个计数器的所有输出是在同一时刻改变的。
将它们的输出分别表示出来,做一个整体,如下图:
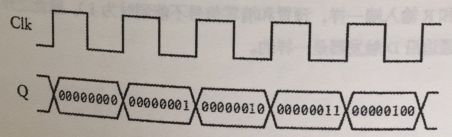
如果把一个振荡器连接到8位计数器的时钟输入端上,那么这个计数器会显示出振荡器经过的循环次数。当计数器总数达到11111111,它又会返回00000000.当这个时候我们记下时间,就是振荡器循环256次所需要的时间,假设这个时间为10s,则振荡器的频率是256÷10,即25.6Hz。
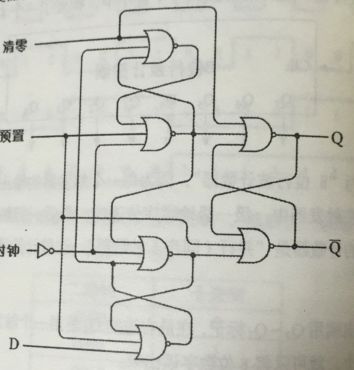
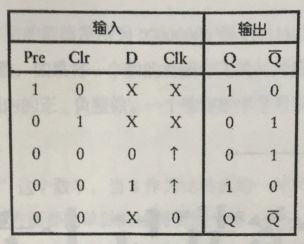
随着触发器功能的增加,它的结构也变得更加复杂。下面是一个带预置和清零功能的边沿型D触发器:
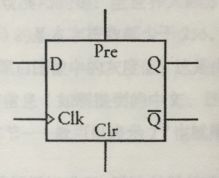
通常情况下,预置和清零信号输入会覆盖时钟和数据端输入,且两个输入都为0,当预置信号为1时,Q变为1,Q反变为0.当清零信号为1,Q变为0,Q反变为1(和R-S触发器中的S和R一样,预置和清零信号不能同时为1)。除此之外,该触发器的工作原理是和普通边沿D触发器是一样的。
电路符号可以简单的用下图来表示:
现在我们所示例用的硬件是100多年前就存在丢东西,我们还有更多东西需要探索。