【数据挖掘】朴素贝叶斯算法计算ROC曲线的面积

题记：

         近来关于数据挖掘学习过程中，学习到朴素贝叶斯运算ROC曲线。也是本节实验课题，roc曲线的计算原理以及如果统计TP、FP、TN、FN、TPR、FPR、ROC面积等等。往往运用ROC面积评估模型准确率，一般认为越接近0.5，模型准确率越低，最好状态接近1，完全正确的模型面积为1.下面进行展开介绍：

---

 

ROC曲线的面积计算原理

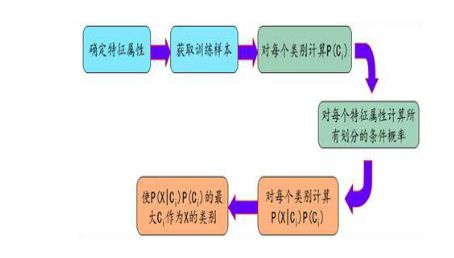
一、朴素贝叶斯法的工作过程框架图

             

二、利用weka工具，找到训练的预处理数据          

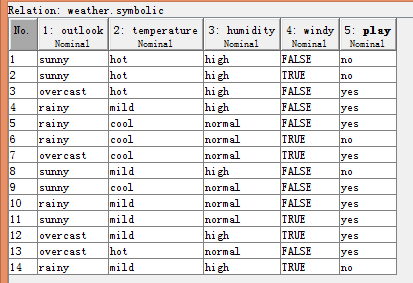
1、利用朴素贝叶斯算法对weather.nominal.arff文件进行处理，然后选择temperature打开，选择编辑找到预处理数据如图1-1所示：

 

图1-1 完整天气数据信息图

2、根据上面的训练元组计算每个类的先验概率，公式为P(C)

     2.1、计算先验概率

            P(play=yes)=9/14=0.643

            P(play=no)=5/14=0.357

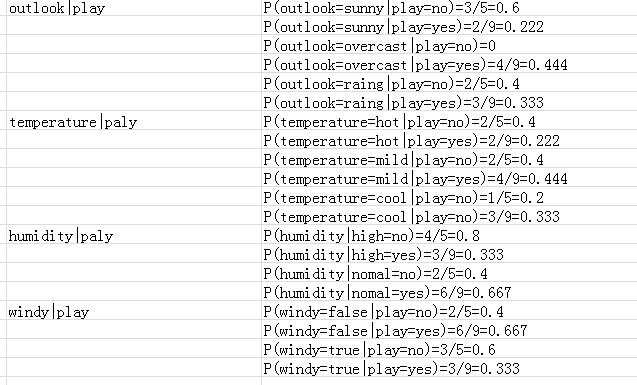
     2.2、 计算条件概率，根据公式P(X|C)

 

3、再根据公式（展示其中一个元组进行概率分类X= (outlook=sunny,temperature=mid,humidity=yes,windy=sunny)）代入上述数据：

      3.1、 P(X|paly=yes)=P(outlook=sunny|play=yes)* P(temperature=mid|play=yes)* P(humidity=yes|play=yes)* P (outlook=sunny|play=yes)）

                同理计算：P(X|paly=no)

       3.2、通过结果比较，得出元组play

       3.3、然后进行概率的计算

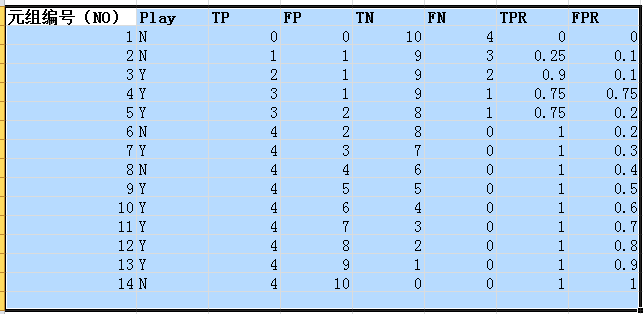
4、再引用《数据挖掘概念与技术》中P244页方法，如图1-2所示：

 

图1-2 返回数据样例

 

如上图为样例非真实数据：因为根据3.3可以计算每个元组的概率，利用概率大小进行类的排序。再根据先验概率进行TP、FP、TN、FN的真实数据，并且不难算出TPR和FPR的数据

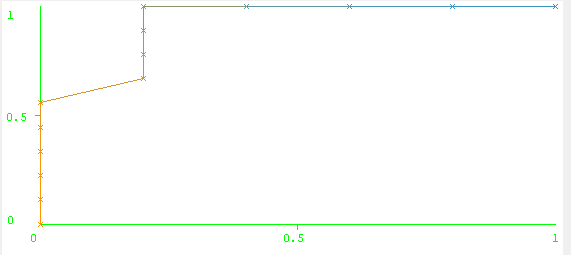
5、再引用《数据挖掘概念与技术》中P245页知识，以FPR作为x轴，TPR作为Y轴，绘制数据的ROC曲线，将4中的数据分别代入进去，得到如图1-3所示：

 

 

图1-3 返回数据图

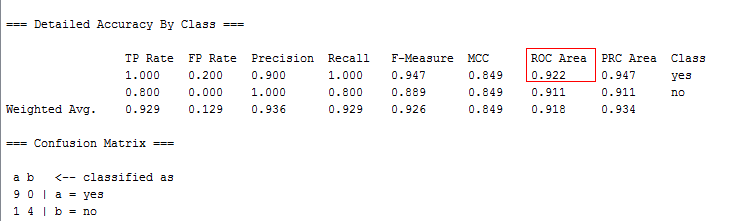
根据以上图形，利用数学方法得到ROC曲线面积为0.9222.然后再利用weka查看工具数据，如图1-4所示：

 

图1-4 weka返回数据

 

。

参考资料：

[1]  使用Weka进行数据挖掘（http://www.cnblogs.com/bluewelkin/p/3538599.html）

[2]  WEKA使用（基础配置+垃圾邮件过滤+聚类分析+关联挖掘） （http://www.cnblogs.com/bitpeach/p/3770606.html）

[3] ROC曲线下面积的计算方法（http://wenku.baidu.com/view/3d2ac9202f60ddccda38a07a.html?re=view）

[4] 韩家炜，数据挖掘概念与技术，P243-P245。

[5] 分类（数据挖掘） （http://wenku.baidu.com/link?url=EdT7Xxs-a_423oM-48ih-KxtTEPrXeejci0-XSM1yk9xbkZGTvWqyiZNpZwUA8a-dlf-kReHlS63u9PXXXuDJFCsdmbpZ2kex5BhwTysWHe&qq-pf-to=pcqq.c2c）