Ternary weight networks 论文笔记

前言

    就目前而言，深度神经网络的层数和训练时间变得越来越多。一方面，人们想要在处理器上面下功夫，但是处理器的处理速度也十分有限。造成目前一个比较深的神经网络的训练时间有时候往往需要一到两周，基于目前的困难，就有人提出了解决方式。
    首先，在神经网络训练的整个训练过程中，最占用时间的无疑是乘法操作。是浮点型数据的乘法尤其消耗计算量，往往需要很多个Clock。那么，如果把所有全连接的权值全部变成1，或者-1的话，乘法运算就变成了简单的加减法，这无疑是非常节约计算时间的。目前的权值简化策略大概分为两种，Binary和Ternary。Binary是把权值简化为1和-1，而Ternary是把权值简化为1，-1,0两者的区别是什么呢？Binary在比较简单的库表现比较好比如说MNIST, CIFAR-10，但是在比较复杂的库比如说ImageNet上表现相对于Ternary有差距。

0 摘要

    我们引入三元权重网络（TWN），这个神经网络的权重被限制为+1，0和-1。 通过最小化全精度（浮点或者双精度）的权重与三元权重之间的欧几里得距离。这种基于阈值的三元函数可以很容易并且快速地被优化，获得近似解。TWN和最近提出的二元权重网络相比有更强的表达能力，而且比后者更有效。相比于全精度权重网络，三元权重网络实现了16×或32×的模型压缩率，而且需要的乘法运算也更少。在MNIST，CIFAR-10和大规模ImageNet数据集的测试表明，TWN的性能仅略差于全精度权重网络，但优于二元权重网络。

1 介绍

     深度神经网络在计算机视觉任务中取得了显著的效果。这激发了将这种最先进的DNN模型部署到智能手机或嵌入式设备等实际应用的兴趣。然而，这些模型通常需要相当大的内存和计算能力，很容易使得小型嵌入式设备的内存，电池电量和计算能力负担过重。 因此，部署它仍然是一项挑战。

1.1 二元权重网络和模型压缩

    为了解决内存和计算能力的问题，一些方法试图在DNN模型中对权重或激活值进行二值化。BinaryConnect 使用符号函数对权重进行二进制化。 XNOR-NET采用相同的二值化函数，但增加了一个额外的比例因子。基于这种二值化方法的扩展BinaryNet和XNOR-NET，它们的权重和激活值都是二元值。这些模型消除了前向传播和后向传播中大部分乘法。因此，用于深度学习的专用硬件可以从中受益。另外，二元权重网络实现高达32×或64×模型压缩率。
     除了采用二值技术，另一些压缩方法的重点在于用更少的参数。通过以有损压缩的方式来保持准确性。 SqueezeNet是一个比AlexNet 参数少50倍的模型，但在ImageNet上保持同AlexNet级别的精度。 深度压缩是另一种最近提出的使用修剪，量化和霍夫曼编码来压缩神经网络的方法。 它将AlexNet和VGG-16的存储需求分别减少了35倍和49倍，而不会降低准确性。

2 三元权值网络（TWN）

     我们通过引入三元权重网络（TWN）来解决有限的内存和有限的计算资源问题。它将权重限制为三值：+1,0和-1。 TWNs试图在全精度权重网络和二元权值网络之间取得平衡。详细的叙述如下：
表达能力：在VGG，GoogLeNet 和残留网络等最新的网络体系结构中，最常用的卷积滤波器大小为3×3。 使用二值权重，有 23×3=512 2 3 × 3 = 512 个模板。 然而，具有相同尺寸的三值权重拥有 33×3=19683 3 3 × 3 = 19683 个模板，其表现能力比二值权重增强了38倍。
模型压缩：在TWN中，每一个权重单元需要2字节的存储空间。 因此，与浮点（32位）或双精度（64位）精度相比，TWN实现了高达16倍或32倍的模型压缩率。 以VGG-19为例，该模型的全浮点权重版本需要约500M的存储需求，三元权值可降至约32M。 因此，虽然三元权值网络的压缩率比二元权值网络的压缩率低2倍，但仍然可以压缩大多数现有的最先进的DNN模型。
计算要求：与二元权值网络相比，TWN拥有额外的0值。 但是，0值不增加任何的乘法运算。 因此，TWN中的乘法累加操作次数与二元权值网络相比保持不变。 而且，它对于专用DL硬件来训练大规模网络也具有友好性。
在下面的部分中，我们将详细描述三元权重网络的问题和一个近似但有效的解决方案。 之后，介绍了一种简单的误差反向传播的训练算法，最后描述了运行时间的使用情况。

2.1 公式

    为了提高三元权值网络的性能，我们最小化全精度权值 W W 和三元权值 Wt W t 之间的欧氏距离。公式如下：

{α∗,Wt∗=argminα,WtJ(α,Wt)=||W−αWt||22s.t.α≥0,Wti∈{−1,0,1},i=1,2,...,n(1) { α ∗ , W t ∗ = a r g m i n α , W t J ( α , W t ) = | | W − α W t | | 2 2 s . t . α ≥ 0 , W i t ∈ { − 1 , 0 , 1 } , i = 1 , 2 , . . . , n ( 1 )

其中，n是卷积核的数量，权重估计 W≈αWt W ≈ α W t 。三元权值网络的前向传播如下：

{Z=X×W≈X×(αWt)=(αX)⨁WtXnext=g(Z)(2) { Z = X × W ≈ X × ( α W t ) = ( α X ) ⨁ W t X n e x t = g ( Z ) ( 2 )

其中， X X 是输入的矩阵块； × × 是卷积运算或内积运算； g g 是非线性激活函数； ⨁ ⨁ 内积或卷积运算，无任何乘法； Xnext X n e x t 是输出的矩阵块。

2.2 三元函数的近似解决方案

    这个算法的核心是只在前向和后向过程中使用使用权值简化，但是在参数更新仍然是使用连续的权值。
    简单的说就是先利用公式计算出三值网络中的阈值：
Δ∗≈0.7×E(|W|)=0.7n∑ni=1|Wi| Δ ∗ ≈ 0.7 × E ( | W | ) = 0.7 n ∑ i = 1 n | W i |
也就是说，将每一层的权值绝对值求平均值乘以0.7算出一个 Δ Δ 作为三值网络离散权值的阈值，具体的离散过程如下：

Wti=ft(Wi|Δ)=⎧⎩⎨+1,0,−1,ifWi>Δif|Wi|≤ΔifWi<−Δ W i t = f t ( W i | Δ ) = { + 1 , i f W i > Δ 0 , i f | W i | ≤ Δ − 1 , i f W i < − Δ

这样，我们就可以把连续的权值变成离散的（1,0，-1），那么，接下来我们还需要一个 α α 参数，具体干什么用后面会说：这个参数的计算方式如下：
α∗Δ=1IΔ∑i∈IΔ|Wi| α Δ ∗ = 1 I Δ ∑ i ∈ I Δ | W i |
|IΔ| | I Δ | 这个参数指的是权值的绝对值大于 Δ Δ 的权值个数，计算出这个参数我们就可以简化前向计算了，具体简化过程如下：

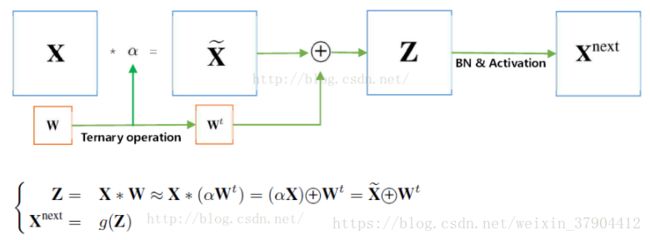
可以看到，在把 α α 乘到前面以后，我们把复杂的乘法运算变成了简单的加法运算，从而加快了整个的训练速度。

2.3 SGD训练

    我们使用随机梯度下降（SGD）方法来训练TWN。 我们在前向传播和反向传播期间使用三值权重，但不在参数更新期间使用。 此外，还采用了两个有用的技巧：批量标准化和学习率衰减。 我们也使用动量。

2.4 模型压缩和运行时间

    运行时达到16倍或32倍模型压缩率。

3 实验

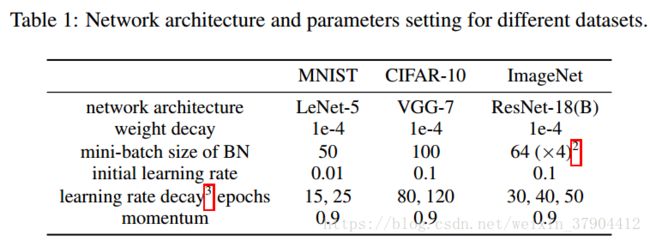
不同数据集上，网络结构和参数如下表：


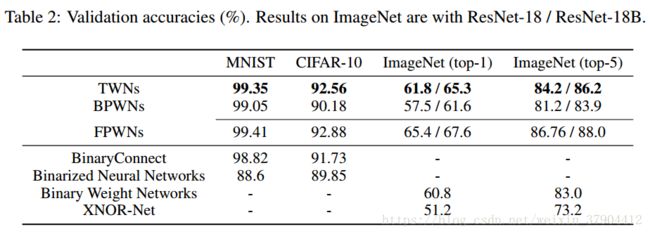
可以看到，其实三值网络在ImageNet这种库上面，虽然效果好于二值网络但是还是不够准确，实际的工作中我们可以考虑在准确率到达一定程度后，再去使用简化权值网络达到加快训练时间同时保护识别精度的效果。