机器学习sklearn之贝叶斯网络实战（一）

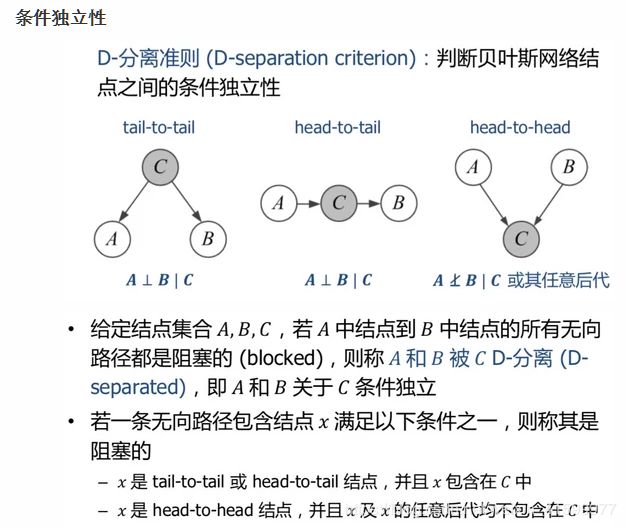
贝叶斯网络

贝叶斯网络、信念网络、贝叶斯模型或概率定向无环图形模型是一种概率图形模型 (一种统计模型), 通过有向无环图 (DAG)表示一组随机变量及其条件依赖关系。

当我们想要表示随机变量之间的因果关系时, 主要使用贝叶斯网络。

贝叶斯网络使用条件概率分布 (CPD) 进行参数化。
网络中的每个节点都使用 $P(node|Pa(node))$, 其中 $Pa(node)$ 表示网络中节点的父节点。

下面绘制网络结构图的时候会有一些无关紧要的警告，很烦人，我给忽略了

import warnings 
warnings.filterwarnings("ignore")

建立一个贝叶斯网络模型需要两个参数：网络模型及概率分布

在 pgmpy 中, 定义一个贝叶斯网的流程一般是先建立网络结构, 然后填入相关参数.

from pgmpy.models import BayesianModel
from pgmpy.factors.discrete import TabularCPD
import networkx as nx
from matplotlib import pyplot as plt
%matplotlib inline

# 构建一个网络模型
model = BayesianModel([('D', 'G'),   # 一条有向边，D ---> G
                       ('I', 'G'),   # I ---> G
                       ('G', 'L'),   # G ---> L
                       ('I', 'S')])  # I ---> S

# 设置CPD参数

# variable='D'：节点名为 D，
# variable_card=2：有两种可能的情况，
# values=[[0.6, 0.4]]：概率分别是0.6和0.4
cpd_d = TabularCPD(variable='D', variable_card=2, values=[[0.6, 0.4]])  

# variable='I'：节点名为I
# variable_card=2：有两种可能的情况，
# values=[[0.7, 0.3]]：概率分别是0.7和0.3
cpd_i = TabularCPD(variable='I', variable_card=2, values=[[0.7, 0.3]])

# In pgmpy the colums are the evidences and rows are the states of the variable.
# 在设置G节点时，结构与上图显示的有点不同，这里，列：evidence 行：state，设置参数时，结构如下表：
#    +---------+---------+---------+---------+---------+
#    | diff    | intel_0 | intel_0 | intel_1 | intel_1 |
#    +---------+---------+---------+---------+---------+
#    | intel   | diff_0  | diff_1  | diff_0  | diff_1  |
#    +---------+---------+---------+---------+---------+
#    | grade_0 | 0.3     | 0.05    | 0.9     | 0.5     |
#    +---------+---------+---------+---------+---------+
#    | grade_1 | 0.4     | 0.25    | 0.08    | 0.3     |
#    +---------+---------+---------+---------+---------+
#    | grade_2 | 0.3     | 0.7     | 0.02    | 0.2     |
#    +---------+---------+---------+---------+---------+

# variable='G'：节点名为 G，
# variable_card=3：有两种可能的情况，
# values=[[0.3, 0.05, 0.9,  0.5],
#        [0.4, 0.25, 0.08, 0.3],
#        [0.3, 0.7,  0.02, 0.2]],：针对不同的父节点的情况组合，具有不同的概率分布，如上表
# evidence=['I', 'D']：父节点为 I 和 D，即 I 和 D 指向 G
# evidence_card=[2, 2]：父节点分别有两种可能的情况
cpd_g = TabularCPD(variable='G', variable_card=3, 
                   values=[[0.3, 0.05, 0.9,  0.5],
                           [0.4, 0.25, 0.08, 0.3],
                           [0.3, 0.7,  0.02, 0.2]],
                  evidence=['I', 'D'],
                  evidence_card=[2, 2])

cpd_l = TabularCPD(variable='L', variable_card=2, 
                   values=[[0.1, 0.4, 0.99],
                           [0.9, 0.6, 0.01]],
                   evidence=['G'],
                   evidence_card=[3])

cpd_s = TabularCPD(variable='S', variable_card=2,
                   values=[[0.95, 0.2],
                           [0.05, 0.8]],
                   evidence=['I'],
                   evidence_card=[2])

# Associating the CPDs with the network
# 将概率分布表加入到贝叶斯网络中
model.add_cpds(cpd_d, cpd_i, cpd_g, cpd_l, cpd_s)

# check_model checks for the network structure and CPDs and verifies that the CPDs are correctly 
# defined and sum to 1.
# 验证模型数据的正确性（检测节点是否定义，概率和是否为1）
model.check_model()

# 绘制网络结构图，并附上概率分布表
nx.draw(model,
        with_labels=True,
        node_size=1000,
        font_weight='bold',
        node_color='y',
        pos={"L": [4, 3], "G": [4, 5], "S": [8, 5], "D": [2, 7], "I": [6, 7]})
plt.text(2, 7, model.get_cpds("D"), fontsize=10, color='b')
plt.text(5, 6, model.get_cpds("I"), fontsize=10, color='b')
plt.text(1, 4, model.get_cpds("G"), fontsize=10, color='b')
plt.text(4.2, 2, model.get_cpds("L"), fontsize=10, color='b')
plt.text(7, 3.4, model.get_cpds("S"), fontsize=10, color='b')
plt.title('test')
plt.show()

# We can now call some methods on the BayesianModel object.
# 查看概率分布
model.get_cpds()

[,
 ,
 ,
 ,
 ]

# 显示某个节点的概率分布
print(model.get_cpds('G'))

+-----+-----+------+------+-----+
| I   | I_0 | I_0  | I_1  | I_1 |
+-----+-----+------+------+-----+
| D   | D_0 | D_1  | D_0  | D_1 |
+-----+-----+------+------+-----+
| G_0 | 0.3 | 0.05 | 0.9  | 0.5 |
+-----+-----+------+------+-----+
| G_1 | 0.4 | 0.25 | 0.08 | 0.3 |
+-----+-----+------+------+-----+
| G_2 | 0.3 | 0.7  | 0.02 | 0.2 |
+-----+-----+------+------+-----+

model.get_cardinality('G')  # G节点可能的情况有几种（基数）

3

独立性分析

从图中可以看出：

• Causal：在给定B的情况下，A,C被阻断，是独立的$ (A \perp C | B) $
• Evidential：在给定B的情况下，A,C是独立的$ (A \perp C | B) $
• Common Evidence：在B未知的情况下，A,C是独立的$ (A \perp C | B) $
• Common Cause：在给定B的情况下，A,C是独立的$ (A \perp C | B) $

import networkx as nx
from matplotlib import pyplot as plt
%matplotlib inline

model2 = BayesianModel([('A', 'B'), ('C', 'B'), ('B', 'D')])

cpd_a = TabularCPD(variable="A", variable_card=2, values=[[0.6, 0.4]])
cpd_c = TabularCPD(variable='C', variable_card=2, values=[[0.7, 0.3]])
cpd_b = TabularCPD(variable='B', variable_card=3, 
                   values=[[0.3, 0.05, 0.9,  0.5],
                           [0.4, 0.25, 0.08, 0.3],
                           [0.3, 0.7,  0.02, 0.2]],
                  evidence=['A', 'C'],
                  evidence_card=[2, 2])
cpd_d = TabularCPD(variable='D', variable_card=2, 
                   values=[[0.1, 0.4, 0.99],
                           [0.9, 0.6, 0.01]],
                   evidence=['B'],
                   evidence_card=[3])

model2.add_cpds(cpd_a, cpd_b, cpd_c, cpd_d)

# 绘制网络结构图
nx.draw(model2,
        with_labels=True,
        node_size=1000,
        font_weight='bold',
        node_color='y',
        pos={"A": [4.9, 4.7], "C": [5.1, 4.7], "B": [5, 4.5], "D": [5, 4.3]})

plt.show()

print("检测模型的正确性：", model2.check_model())

检测模型的正确性： True

print("独立性分析：\n", model2.local_independencies(['D']))
print(model2.local_independencies('B'))  # 没有输出，B与其他节点都相关
print(model2.local_independencies('A'))
print(model2.local_independencies('C'))

独立性分析：
 (D _|_ C, A | B)

(A _|_ C)
(C _|_ A)

第一个案例里的贝叶斯网络的独立性分析

model.local_independencies('G')

(G _|_ S | D, I)

model.local_independencies(['D', 'I', 'S', 'G', 'L'])

(D _|_ I, S)
(I _|_ D)
(S _|_ L, D, G | I)
(G _|_ S | D, I)
(L _|_ D, I, S | G)

# Active trail: For any two variables A and B in a network if any change in A influences the values of B then we say
#               that there is an active trail between A and B.
# In pgmpy active_trail_nodes gives a set of nodes which are affected by any change in the node passed in the argument.
model.active_trail_nodes('D')  # 当 D 节点发生变化时，受影响的节点

{'D': {'D', 'G', 'L'}}

model.active_trail_nodes('D', observed='G')  # 当 D 节点发生变化时且 G 节点已知，受影响的节点

{'D': {'D', 'I', 'S'}}

联合概率

Till now we just have been considering that the Bayesian Network can represent the Joint Distribution without any proof. Now let’s see how to compute the Joint Distribution from the Bayesian Network.

From the chain rule of probabiliy we know that:联合概率的求解公式如下：
$$P(A,B)=P(A|B)\ast P(B)$$

Now in this case:在本次案例中，计算所有贝叶斯网络的联合概率
$$P(D,I,G,L,S)=P(L|S,G,D,I)\ast P(S|G,D,I)\ast P(G|D,I)\ast P(D|I)\ast P(I)$$

Applying the local independence conditions in the above equation we will get:使用上述分子的局部独立条件，得到的联合概率公式为：
$$P(D,I,G,L,S)=P(L|G)\ast P(S|I)\ast P(G|D,I)\ast P(D)\ast P(I)$$
总结：在贝叶斯网络里计算联合概率：一个节点的所有父亲节点作为条件的条件概率相乘：

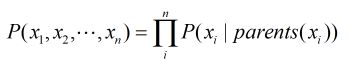
From the above equation we can clearly see that the Joint Distribution over all the variables is just the product of all the CPDs in the network. Hence encoding the independencies in the Joint Distribution in a graph structure helped us in reducing the number of parameters that we need to store.

贝叶斯模型的推断

Till now we discussed just about representing Bayesian Networks. Now let’s see how we can do inference in a Bayesian Model and use it to predict values over new data points for machine learning tasks. In this section we will consider that we already have our model. We will talk about constructing the models from data in later parts of this tutorial.

In inference we try to answer probability queries（概率查询） over the network given some other variables. So, we might want to know the probable grade of an intelligent student in a difficult class given that he scored good in SAT. So for computing these values from a Joint Distribution we will have to reduce over the given variables that is $I=1$, $D=1$, $S=1$ and then marginalize over the other variables that is $L$ to get $P(G|I=1,D=1,S=1)$. But carrying on marginalize and reduce operation on the complete Joint Distribution is computationaly expensive since we need to iterate over the whole table for each operation and the table is exponential is size to the number of variables. But in Graphical Models we exploit the independencies to break these operations in smaller parts making it much faster.

One of the very basic methods of inference in Graphical Models is Variable Elimination.
Variable Elimination

由贝叶斯的联合概率：
$P(D,I,G,L,S)=P(L|G)\ast P(S|I)\ast P(G|D,I)\ast P(D)\ast P(I)$

计算G的概率，我们需要边缘化所有其他变量
$P(G)={\sum }_{D,I,L,S}P(D,I,G,L,S)$ 说明：在知道所有其他变量D、I、L、S的联合概率不就是G的概率吗？

带入上式的联合概率得：
$P(G)={\sum }_{D,I,L,S}P(L|G)\ast P(S|I)\ast P(G|D,I)\ast P(D)\ast P(I)$

由局部独立条件化简得：
$P(G)={\sum }_D{\sum }_I{\sum }_L{\sum }_{S}P(L|G)\ast P(S|I)\ast P(G|D,I)\ast P(D)\ast P(I)$

Now since not all the conditional distributions depend on all the variables we can push the summations inside:
由于并不是所有的条件分布都依赖于所有变量，所以可以变换一下：
$P(G)={\sum }_D{\sum }_I{\sum }_L{\sum }_{S}P(L|G)\ast P(S|I)\ast P(G|D,I)\ast P(D)\ast P(I)$

最后将求和推到里面，可以简化大量的计算
$P(G)={\sum }_{D}P(D){\sum }_{I}P(G|D,I)\ast P(I){\sum }_{S}P(S|I){\sum }_{L}P(L|G)$

from pgmpy.inference import VariableElimination
infer = VariableElimination(model)
print(infer.query(['G'])['G'])

+-----+----------+
| G   |   phi(G) |
+=====+==========+
| G_0 |   0.3620 |
+-----+----------+
| G_1 |   0.2884 |
+-----+----------+
| G_2 |   0.3496 |
+-----+----------+

计算条件分布： $P(G|D=0,I=1)$.

$P(G|D=0,I=1)={\sum }_L{\sum }_{S}P(L|G)\ast P(S|I=1)\ast P(G|D=0,I=1)\ast P(D=0)\ast P(I=1)$

$P(G|D=0,I=1)=P(D=0)\ast P(I=1)\ast P(G|D=0,I=1)\ast {\sum }_{L}P(L|G)\ast {\sum }_{S}P(S|I=1)$

在pgmpy 中，只需要传递一个额外的参数evidence。

print(infer.query(['G'], evidence={'D': 0, 'I': 1})['G'])

+-----+----------+
| G   |   phi(G) |
+=====+==========+
| G_0 |   0.9000 |
+-----+----------+
| G_1 |   0.0800 |
+-----+----------+
| G_2 |   0.0200 |
+-----+----------+

Predicting values from new data points

Predicting values from new data points is quite similar to computing the conditional probabilities. We need to query for the variable that we need to predict given all the other features. The only difference is that rather than getting the probabilitiy distribution we are interested in getting the most probable state of the variable.

当预测新数据时，在给定所有其他特征的基础下，预测的是一个状态值，而不是概率分布

在pympy中，使用map_query()进行预测

infer.map_query(['G'])

{'G': 0}

infer.map_query(['G'], evidence={'D': 0, 'I': 1})

{'G': 0}

infer.map_query(['G'], evidence={'D': 0, 'I': 1, 'L': 1, 'S': 1})

{'G': 0}

print(infer.query(['G'], evidence={'D': 0, 'I': 1, 'L': 1, 'S': 1})['G'])
infer.map_query(['G'], evidence={'D': 0, 'I': 1, 'L': 1, 'S': 1})

+-----+----------+
| G   |   phi(G) |
+=====+==========+
| G_0 |   0.9438 |
+-----+----------+
| G_1 |   0.0559 |
+-----+----------+
| G_2 |   0.0002 |
+-----+----------+

{'G': 0}