数据结构:手撕二分搜索树
文章目录
- 1. 树结构基础
- 2. 创建二分搜索树
- 3. 二分搜索树的添加
- 4. 二分搜索树的查询
- 4.1 前序遍历
- 4.2 中序遍历
- 4.3 后序遍历
- 4.4 层序遍历
- 5.二叉搜索树的删除
- 5.1 查询最小/最大值
- 5.2 删除最小/大值
- 5.3 删除任意节点
- 6. 向上取整(floor)和向下取整(ceil)
- 7. 排名(rank)
- 8. 选择(select)
- 9. 使用BST实现Set集合
- 10. 二叉搜索树的复杂度分析
- 11. 使用二分搜索树实现Map
1. 树结构基础
树和链表一样是属于动态数据结构。
二叉树(二分树)的本意就是对于每个节点最多有左右两个节点,这就是分成二叉。当然也有三叉,四叉等多叉树。
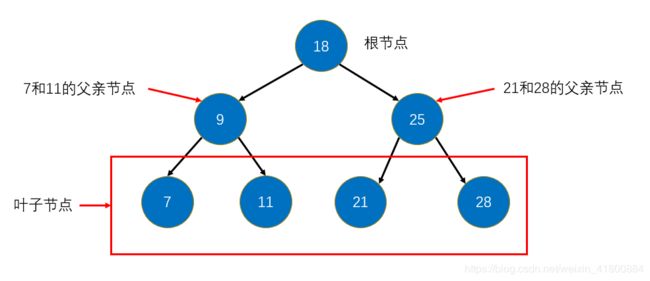
二叉树的特点:
- 具有唯一一个根节点。
- 每个节点最多有左右两个节点(孩子)。
- 每个节点最多只有一个父亲节点,除了根节点。
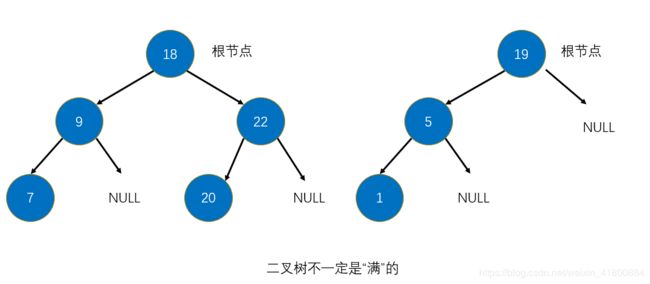
- 除最后一层无任何子节点外,每一层上的所有节点都有两个子节点的二叉树叫做满二叉树。下图就是一个满二叉树。
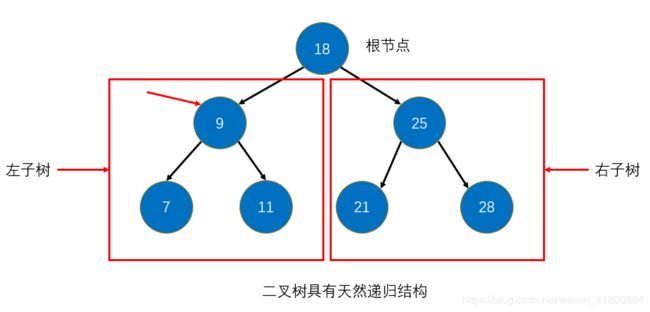
- 每个节点的左节点那一分支的子树其实也是一棵二叉树,叫做左子树,右节点也是,叫做右子树。
二分搜索树(Binary Search Tree)是二叉树,它要求每个节点的值(value):
- 大于其左子树的所有节点的值。
- 小于其右子树的所有节点的值。
- 每个节点的值具有可比较性(Comparable)。
2. 创建二分搜索树
先来看看节点的结构,它需要一个来存储值的变量,还需要左右两个节点:
class Node {
private E e;
private Node left, right;
public Node(E e) {
this.e = e;
this.left = null;
this.right = null;
}
}
那么对于树来说,需要有一个根节点,额外的还可以定义一个size来记录一颗树有多少个节点。把Node封装到二分搜索树中:
/**
* 存储的值具有可比较性,所以需要指定传入的值是Comparable子类
* @param
*/
public class BST<E extends Comparable<E>> {
private class Node {
private E e;
private Node left, right;
public Node(E e) {
this.e = e;
this.left = null;
this.right = null;
}
}
private Node root;
private int size;
public BST() {
root = null;
size = 0;
}
public int getSize() {
return size;
}
public boolean isEmpty() {
return size == 0;
}
}
3. 二分搜索树的添加
注意:根据定义,该二分搜索树是不包含重复元素的。所以如果想包含重复元素,则需要修改定义:左子树小于等于节点;或右子树小于等于节点。
最直观的写法如下:
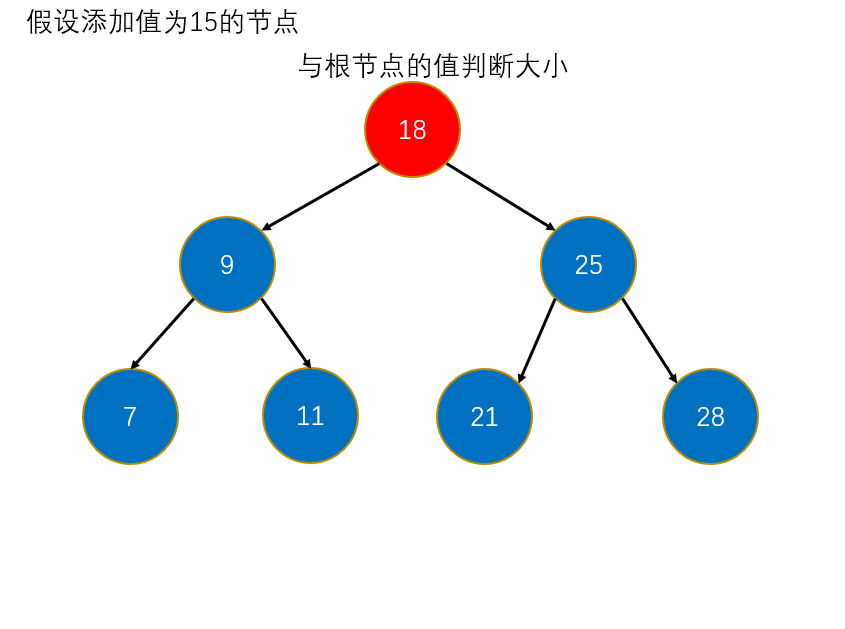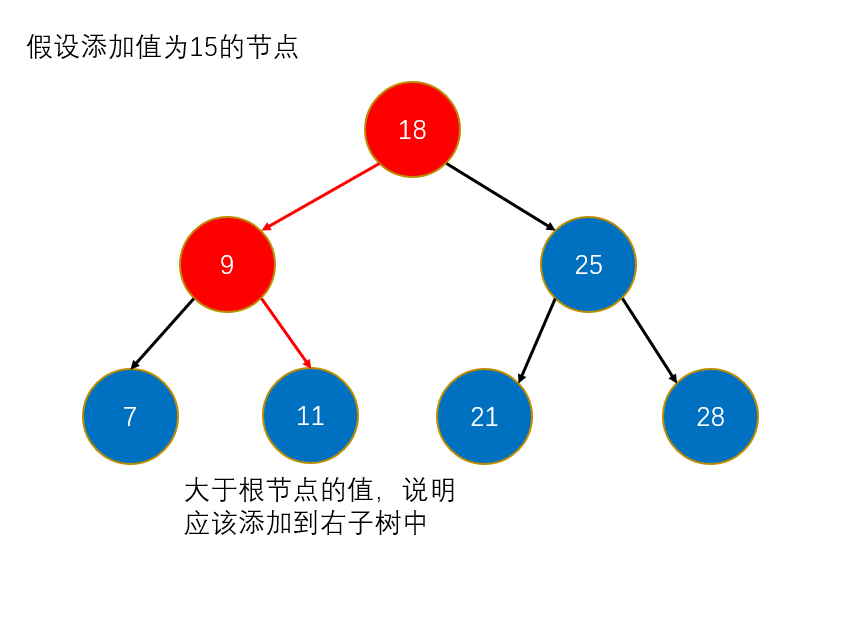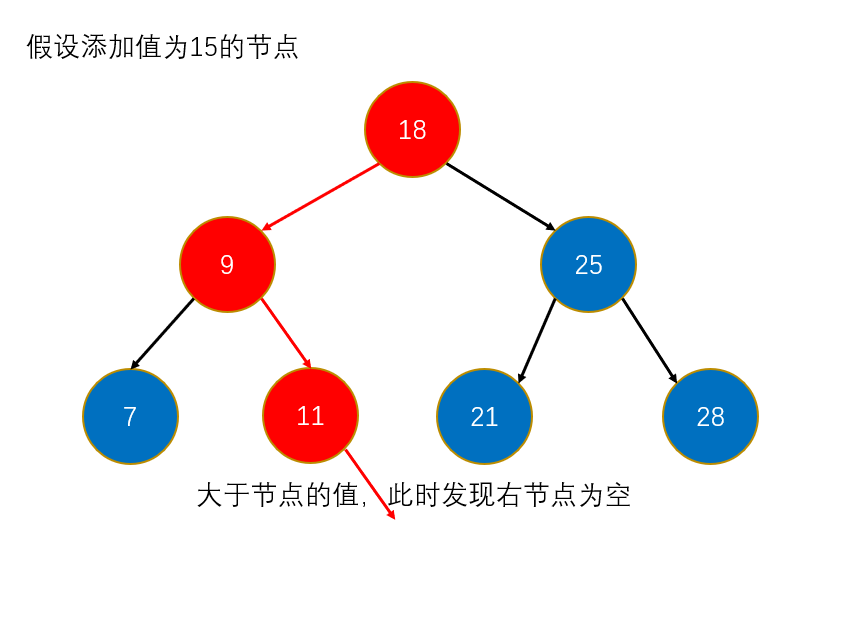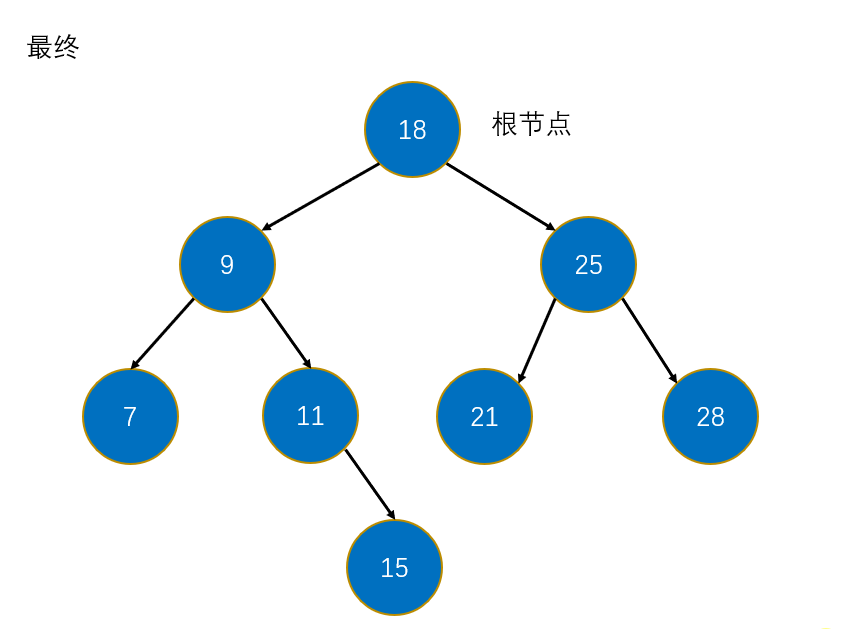
- 先判断根节点,如果为空,直接new一个新的节点。
- 否则,新插入的值就与根节点的值判断大小,如果大于根节点的值,则新插入的值肯定是在右子树,此时判断根节点的右节点是否为null,如果为null,说明新值可以插入到该位置,那么就可以结束了添加操作。如果小于根节点的值,则新插入的值肯定是在左子树,此时判断根节点的左节点是否为null,如果为null,说明新值可以插入到该位置,那么就可以结束了添加操作。如果遇到的值与根节点的值相等,那么不操作,直接结束添加操作。(递归终止条件)
- 如果第二步不成立,那么说明新插入的值得在根节点的左子树或右子树中。此时还得判断新插入的值与根节点的值判断大小,如果小于该根节点的值,则新插入的值肯定在左子树,那么递归跳转到左子树中,否则肯定在右子树插入。
public void add(E e) {
if(root == null) {
root = new Node(e);
size++;
return;
} else {
add(root, e);
}
}
private void add(Node node, E e) {
// 终止条件
// 每次递归,跟根节点的值比较
if(e.compareTo(node.e) == 0) {
return;
} else if(e.compareTo(node.e) < 0 && node.left == null) {
// 如果根节点的值小于e
// 加到左子节点
node.left = new Node(e);
size++;
return;
} else if(e.compareTo(node.e) > 0 && node.right == null) {
// 如果根节点的值大于e
// 加到右子节点
node.right = new Node(e);
size++;
return;
}
if(e.compareTo(node.e) < 0) {
// 如果根节点的值小于e
// 跳转到左子树
add(node.left, e);
} else {
// 如果根节点的值大于e
// 跳转到右子树
add(node.right, e);
}
现在看看上面的写法,是非常清晰的,但是对于代码量还可以再优化,上面冗余的地方就是递归的终止条件,每次递归一次就要先进行三次判断。通过跳转子树的语句可以发现,最终会递到新值插入的位置,也就是递归一直递到树底,那么此时树底肯定是null,供我们插入新的节点,所以可以这样修改:
public void add(E e) {
root = add(root, e);
}
/**
* 每次递归会返回一颗新树
* 直接递归到树底,此时该位置就是新插入的节点的最终位置
* 因为每次递归时,会把当前的根节点的值和要插入的值比较:
* 1. 如果大于根节点,那么新插入的值肯定是要插入到根节点的右子树中
* 2. 如果小于根节点,那么新插入的值肯定是要插入到根节点的左子树中
*
* 因为新插入的节点会改变原先树的结构,因为相比原先多了个节点嘛
* 所以必须维护把旧树替换成新的树
* @param root
* @param e
* @return 返回新节点插入后新树的根
*/
private Node add(Node node, E e) {
// 一个null也可以看成一个节点,也可以看成一颗树
// 递归到底部,直到遇到null就创建节点,把它当成一棵树,然后就返回该树的根
if(node == null) {
size++;
return new Node(e);
}
if(e.compareTo(node.e) < 0) {
// 如果是左子树,add返回新插入节点后的新左子树的根,那么替换掉旧树
node.left = add(node.left, e);
} else if(e.compareTo(node.e) > 0) {
// 如果是右子树,add返回新插入节点后的新右子树的根,那么替换掉旧树
node.right = add(node.right, e);
}
// 返回根
return node;
}
图解:
4. 二分搜索树的查询
对于节点的查询需要结合键值对,以键来查值,后续讲。
打印整颗二分搜索树有4种方式:前序遍历,中序遍历,后续遍历,层序遍历。
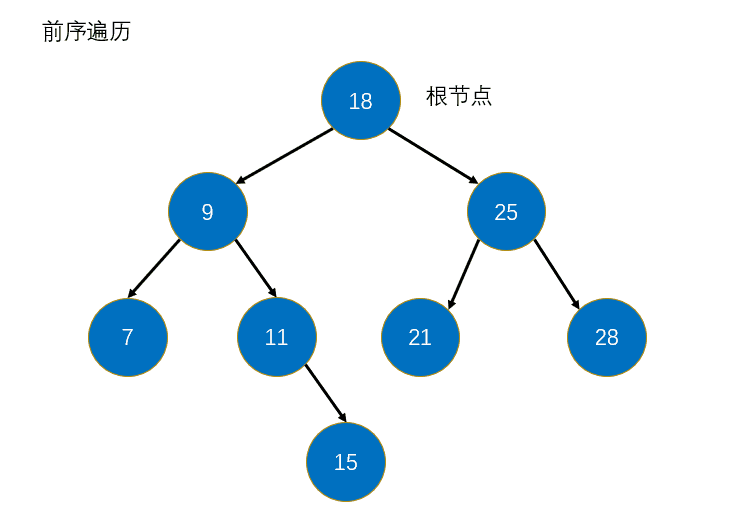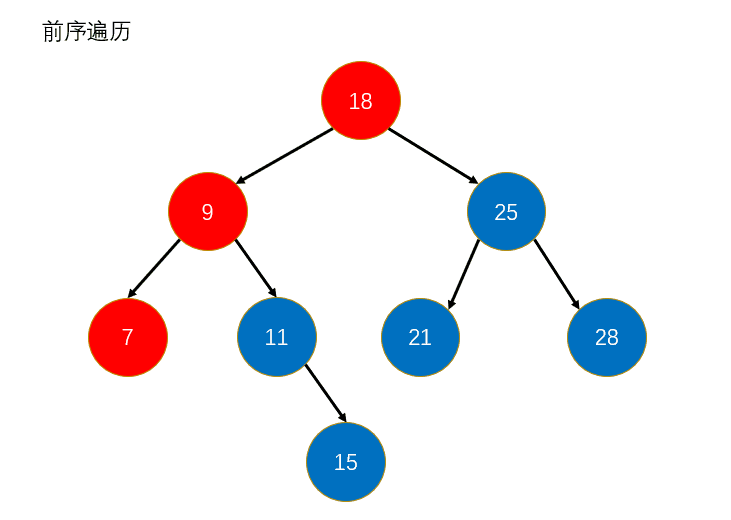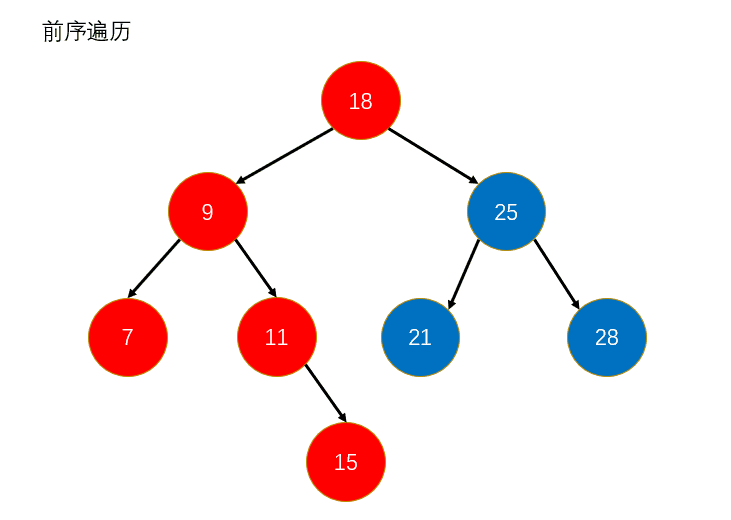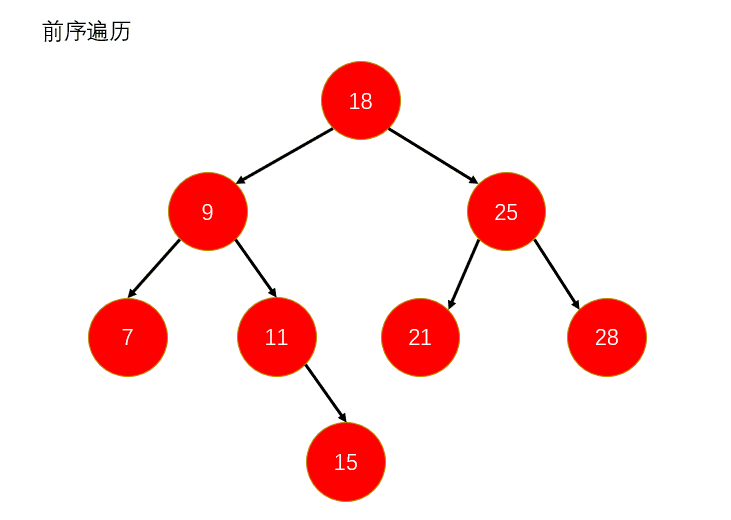
4.1 前序遍历
说白了就是先访问根节点,再去访问左节点,然后去访问右结点。
/**
* 前序遍历
*/
public void preOrder() {
preOrder(root);
}
private void preOrder(Node node) {
if(node != null) {
System.out.println(node.e);
preOrder(node.left);
preOrder(node.right);
}
}
非递归写法:
/**
* 非递归的前序遍历
* 借助栈,注意是先压入右节点再压入左节点
* 这样左节点就在栈顶,下次就先取出左节点
*/
public void preOrderNB() {
Stack<Node> stack = new Stack<>();
stack.push(root);
while(!stack.isEmpty()) {
Node node = stack.pop();
System.out.println(node);
// 先压入右节点
if(node.right != null) {
stack.push(node.right);
}
// 再压入左节点
if(node.left != null) {
stack.push(node.left);
}
}
}
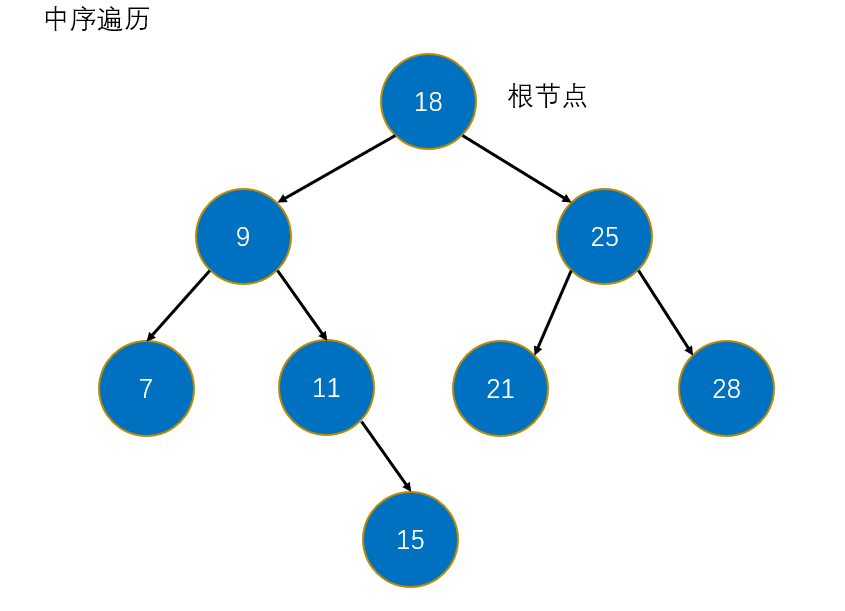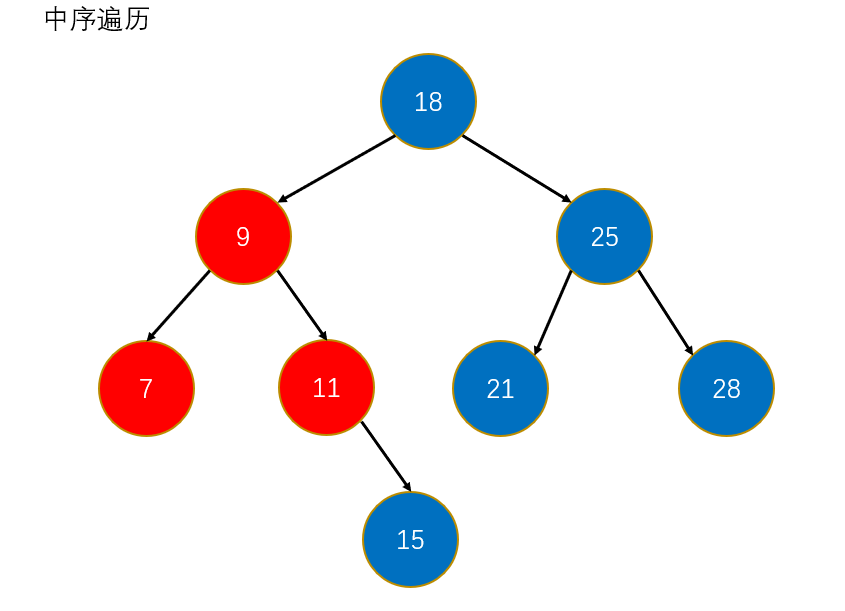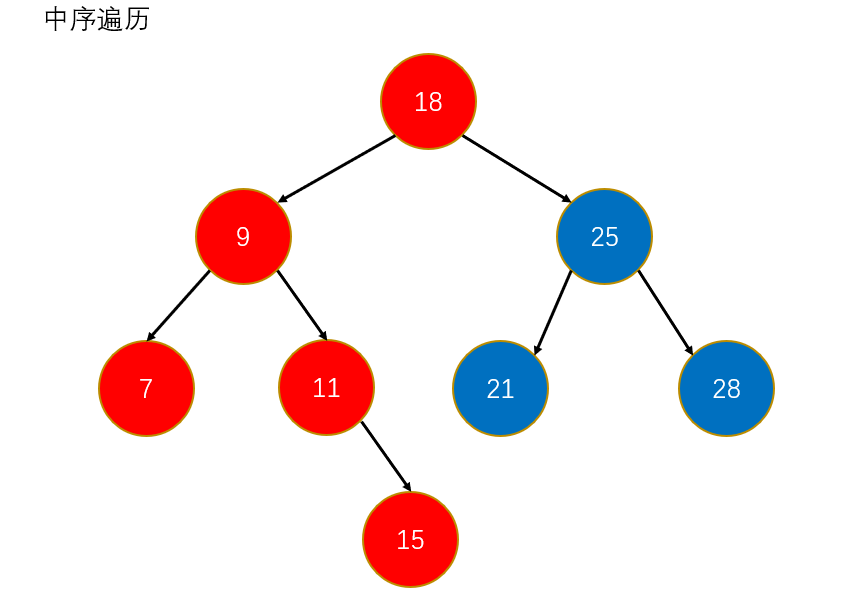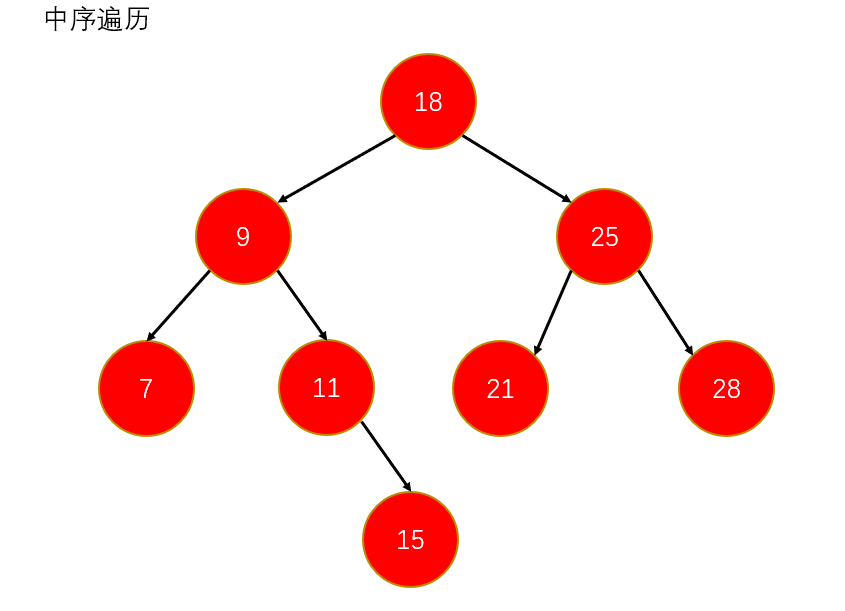
4.2 中序遍历
先访问左节点,然后去访问根节点,再去访问右结点。**中序遍历的结果其实树中所有值排序后的结果。**因为左子树的所有值小于根节点,根节点小于右子树所有值。
/**
* 中序遍历
*/
public void inOrder() {
inOrder(root);
}
private void inOrder(Node node) {
if(node == null) {
return;
}
inOrder(node.left);
System.out.println(node.e);
inOrder(node.right);
}
中序遍历的非递归实现:
/**
* 中序遍历非递归写法
* 还是借助栈,但这次我们是先打印左节点。
* 1. 因为是要先打印根节点的左节点,那么第一个打印的肯定是树中的最小值,即左下角的节点,当然提前是存在左节点。
* 2. 那么我们可以先把根节点的全部左节点压入栈,然后再弹出。
* 3. 对于根节点的右节点有两种情况:
* - 如果根节点的右节点存在,则重复上面的操作。
* - 如果根节点的右节点不存在,则结束。
* 4. 当栈为空时结束。
*/
public void inOrderNR() {
inOrder(root);
}
private void inOrderNR(Node node) {
Stack<Node> stack = new Stack<>();
Node cur = node;
while(!stack.isEmpty()) {
// 以cur为根的树,先把它的全部左节点先压入栈
while(cur != null) {
stack.push(cur);
cur = cur.left;
}
// 栈顶弹出
cur = stack.pop();
// 打印左节点
System.out.println(cur.e);
// 跳到刚刚打印左节点的右子节点中
// 不用判断存不存在,因为根据上面的逻辑,如果不存着右节点,则栈会弹出上一个左节点。
cur = cur.right;
}
}
4.3 后序遍历
先访问左节点,然后去访问右结点,再去访问根节点。
后序遍历的一个应用是:为二分搜索树释放内存。java中是自动释放内存的。C++就可能需要手动释放。
/**
* 后序遍历
*/
public void postOrder() {
postOrder(root);
}
private void postOrder(Node node) {
if(node != null) {
postOrder(node.left);
postOrder(node.right);
System.out.println(node.e);
}
}
后序遍历的非递归实现更复杂。后序遍历的复杂地方就是:必须保证根节点的左子树和右子树被访问后才可以打印根节点。所以需要一个标记位pos,来保存右节点已经被访问的情况。
/**
* 后序遍历非递归写法
* 后序遍历的复杂地方就是:必须保证根节点的左子树和右子树被访问后才可以打印根节点
* 访问根节点的可能有两种情况:根节点的右节点为空,或者右节点已经被访问过
* 所以需要一个标记位pos,来保存右节点已经被访问的情况
*/
public void postOrderNR() {
postOrderNR(root);
}
private void postOrderNR(Node node) {
Stack<Node> stack = new Stack<>();
Node cur = node;
Node pos = null;
while(cur != null || !stack.isEmpty()) {
// 以cur为根的树,先把它的全部左节点先压入栈
while(cur != null) {
stack.push(cur);
cur = cur.left;
}
// 查看栈顶,这里得申请一个临时变量,如果使用cur来存储,那么当打印根节点时,下次循环的cur不为空会出错
Node temp = stack.peek();
// 如果根节点的右节点为空,或者右节点已经被访问过
if(temp.right == null || temp.right == pos) {
// 打印根节点
System.out.println(temp.e);
// 保存已经被访问过的点
pos = stack.pop();
} else {
cur = temp.right;
}
}
}
还是不懂的建议拿个例子试试,我也有图解,但是图片太多了发在这占太多空间,可以下载我写的PPT:蓝奏云
也可以看B站视频,我不小心看到的,虽然跟我的写法有点不一样,但是思路一样的:点我跳转
4.4 层序遍历
把数分层,然后一层一层地打印。
/**
* 层序遍历/广度遍历
*
* queue:
* 1. offer 添加元素,队列满则返回false,poll 移除队头且返回队头,队列为空返回true
* 2. add 添加元素,队列满则抛出一个IIIegaISlabEepeplian异常, remove 移除队头且返回队头,队列为空则抛出一个NoSuchElementException异常
*/
public void levelOrder() {
Queue<Node> queue = new LinkedList<>();
queue.add(root);
while(!queue.isEmpty()) {
Node cur = queue.remove();
System.out.println(cur.e);
if(cur.left != null) {
queue.add(cur.left);
}
if(cur.right != null) {
queue.add(cur.right);
}
}
}
5.二叉搜索树的删除
因为要删除任意节点有点复杂,那么先来说说如何查询最小/大值,然后再引入删除最小/大值,最后再来删除任意节点就比较好理解。
5.1 查询最小/最大值
- 二叉搜索树的最小值一定是在树的左下角。所以要查询时,一直往树的左节点找,直到左节点的下一个左节点为null,说明此时的左节点就是最小值。
- 而最大值一定在树的右下角。查询一直往树的右节点找,直到右节点的下一个右节点为null,说明此时的右节点就是最大值。
/**
* 查询二叉搜索树的最小值
* 一直向左节点走,直到左节点的下一个左节点为null,说明该左节点就是最小值
* @return
*/
public E minimun() {
if(size == 0) {
throw new IllegalArgumentException("Tree is empty.");
}
return minimun(root).e;
}
private Node minimun(Node node) {
if(node.left == null) {
return node;
} else {
return minimun(node.left);
}
}
/**
* 查询二叉搜索树的最大值
* 一直向右节点走,直到右节点的下一个右节点为null,说明该右节点就是最大值
* @return
*/
public E minimax() {
if(size == 0) {
throw new IllegalArgumentException("Tree is empty.");
}
return minimax(root).e;
}
private Node minimax(Node node) {
if(node.right == null) {
return node;
} else {
return minimax(node.right);
}
}
5.2 删除最小/大值
知道了如何查询最小/大值,那么要删除就容易了,但是要注意:
- 对于删除最小值,删除后还要注意删除的节点有没有右节点,如果有,那得把右节点接到原树中,以免数据丢失,至于怎么接,可以把要删除的节点替换成要删除的节点的右节点。这一步也间接地处理了对于要删除的节点没有左右节点的情况,因为对于这种情况我们得把要删除的节点的父亲节点的left指向null,表示删除。
- 对于删除最大值也如此,如果要删除的节点有左节点,那么必须把左节点接回树中。
/**
* 按照常规的,删除后返回删除的元素,
* 1. 先把要删除的最小值查出来
* 2. 然后就删除,因为删除后会改变树的结构,所以得更新root
* 删除细节:删除最小元素,注意要删除的节点有右节点的情况,因为如果删除的节点不把右节点接到树中,会丢失数据。
* @return
*/
public E removeMin() {
E ret = minimun();
root = removeMin(root);
return ret;
}
/**
* 删除最小值
* @param node
* @return 删除后返回以node为根的树
*/
private Node removeMin(Node node) {
if(node.left == null) {
// 此时把要删除的节点的右节点保存起来,不用管有没有
Node rightNode = node.right;
// 这里断开要删除的右节点,防止成环
node.right = null;
size--;
// 然后把要删除的右节点返回,替换掉要删除的节点,这就成功删除了
return rightNode;
}
// 在最后一步,removeMin会把要删除的节点的右节点返回到这,把node.left替换掉,完成删除
// 因为此时是改变左子树的结构,所以要把新树的根返回给左子树
node.left = removeMin(node.left);
return node;
}
/**
* 按照常规的,删除后返回删除的元素,
* 1. 先把要删除的最大值查出来
* 2. 然后就删除,因为删除后会改变树的结构,所以得更新root
* 删除细节:删除最大元素,注意要删除的节点有左节点的情况,因为如果删除的节点不把左节点接到树中,会丢失数据。
* @return
*/
public E removeMax() {
E ret = minimax();
root = removeMax(root);
return ret;
}
/**
* 删除最大值
* @param node
* @return 删除后返回以node为根的树
*/
private Node removeMax(Node node) {
if(node.right == null) {
// 此时把要删除的节点的左节点保存起来,不用管有没有
Node leftNode = node.left;
// 这里断开要删除的左节点,防止成环
node.left = null;
size--;
// 然后把要删除的左节点返回,替换掉要删除的节点,这就成功删除了
return leftNode;
}
// 在最后一步,removeMin会把要删除的节点的左节点返回到这,把node.right替换掉,完成删除
// 因为此时是改变右子树的结构,所以要把新树的根返回给右子树
node.right = removeMax(node.right);
return node;
}
删除最小值图解:
删除最大值的图解相反,不放了。
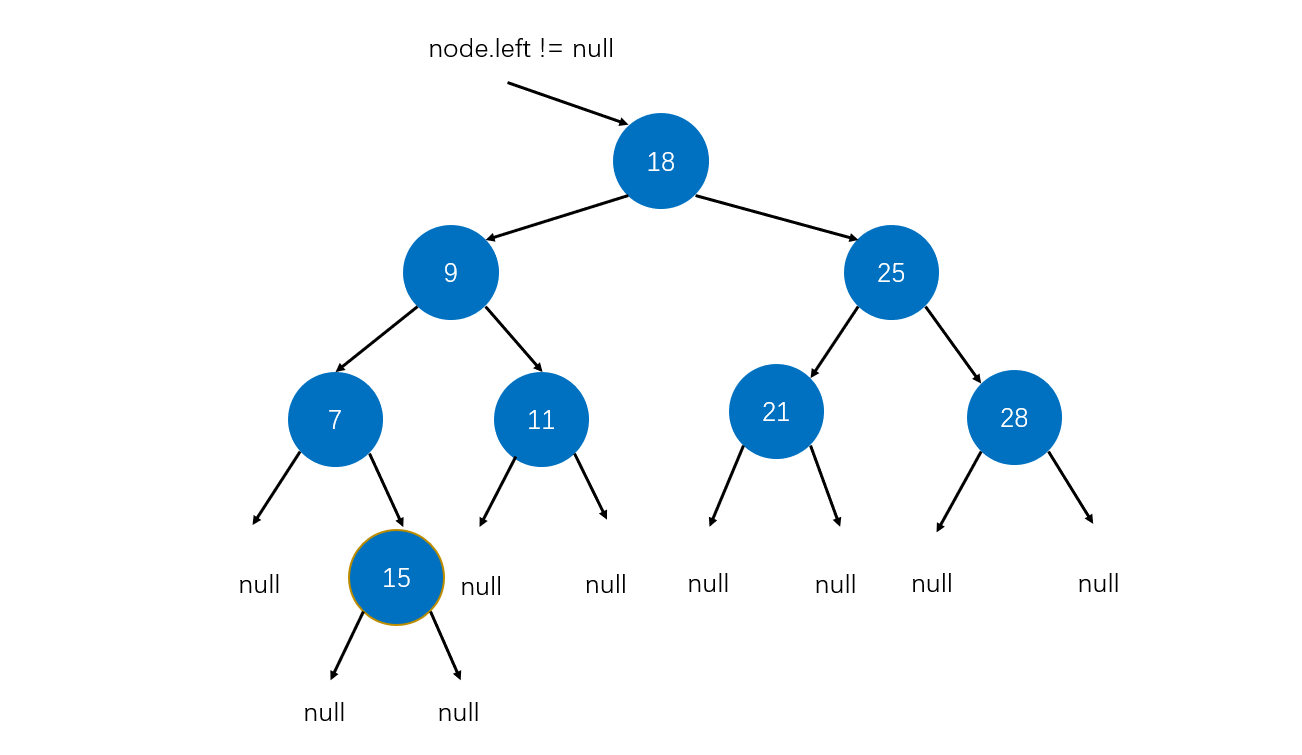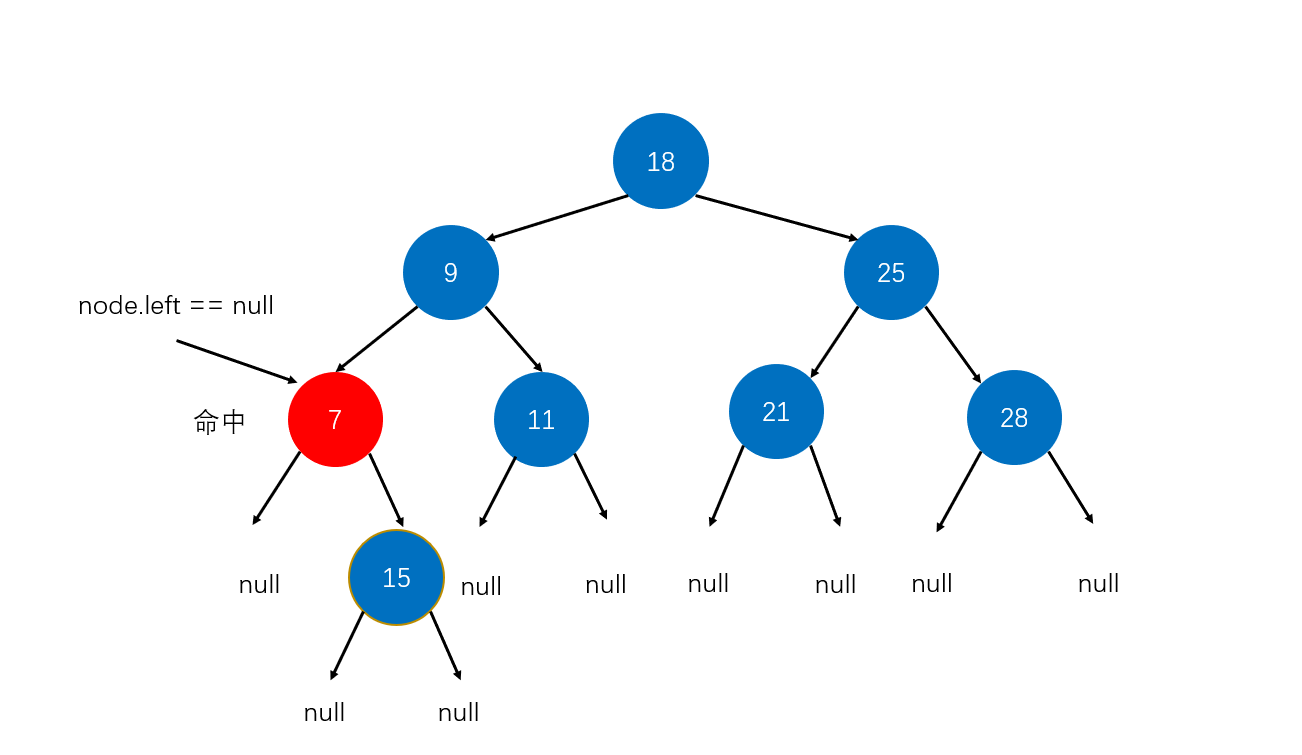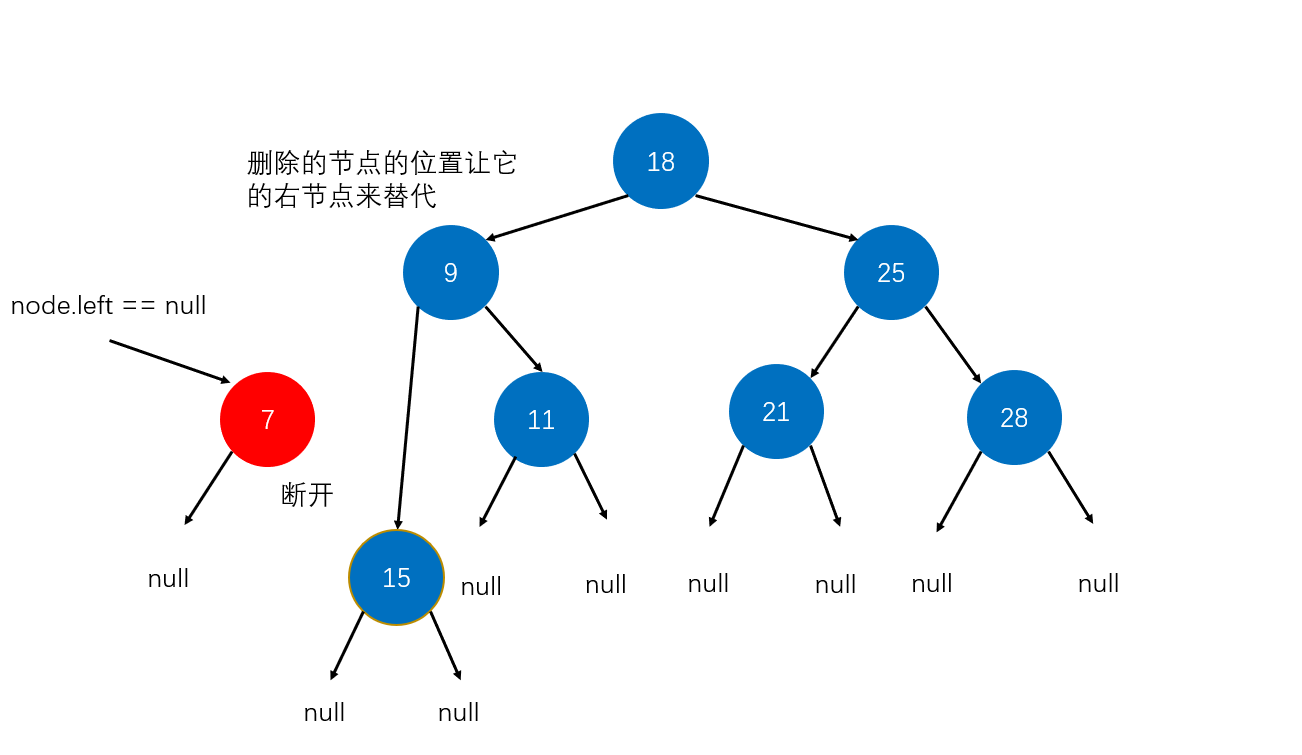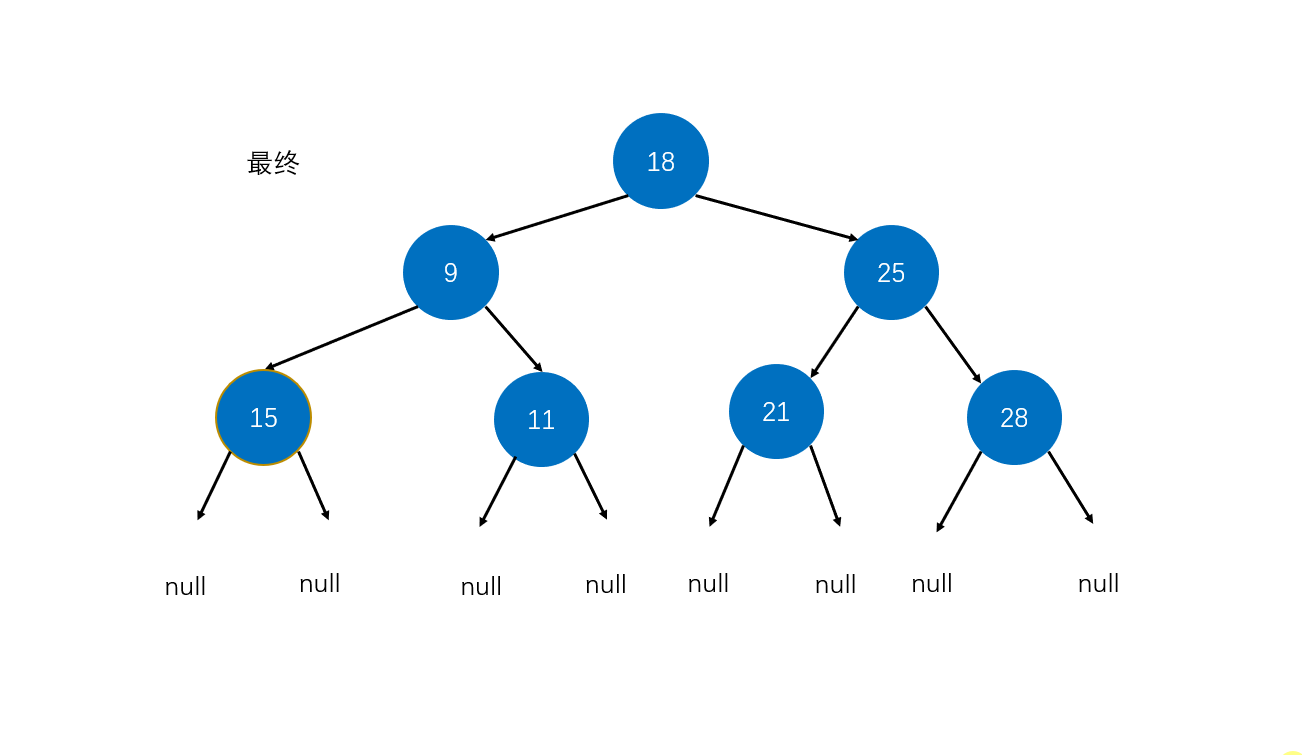
5.3 删除任意节点
删除任意节点,其实有三种情况,即要删除的节点有左右节点,或者有左右节点之一,或者没有左右节点。对于有左右节点之一和没有左右节点的这两种情况可以一起处理,用替换法,上面删除最小值也有说了。
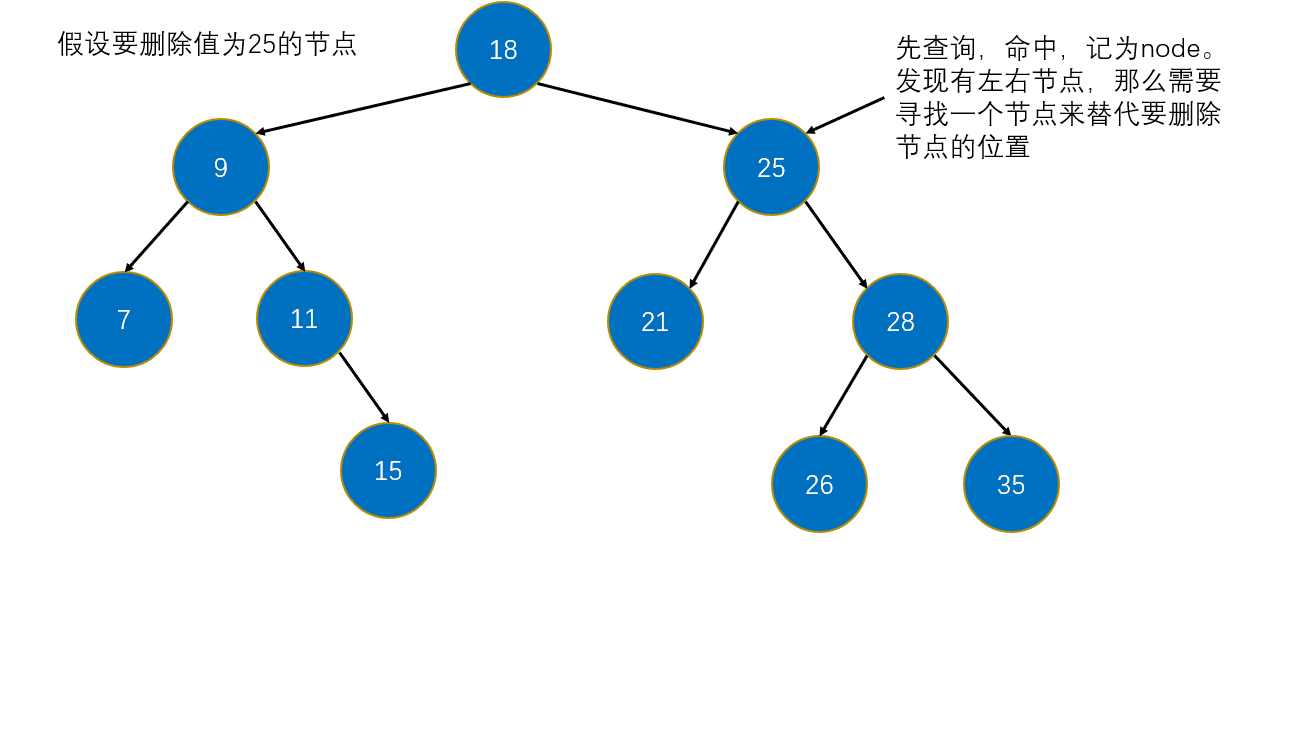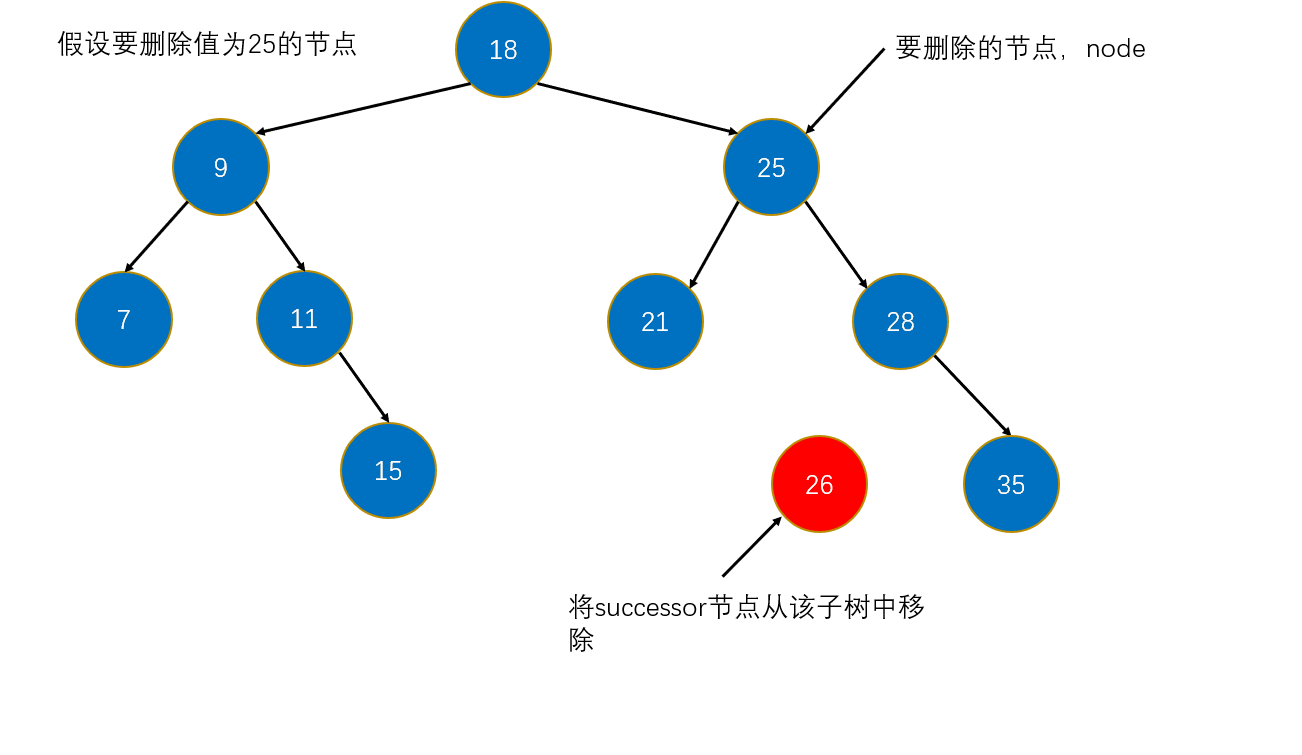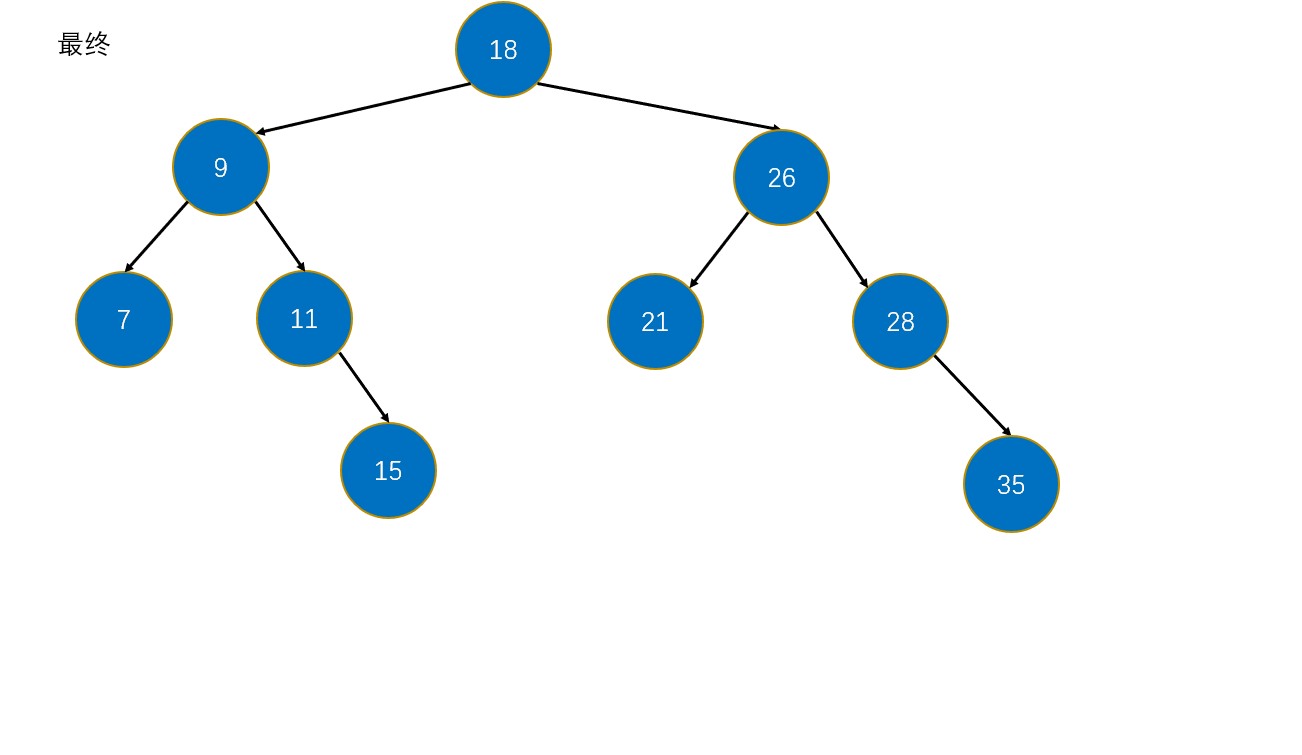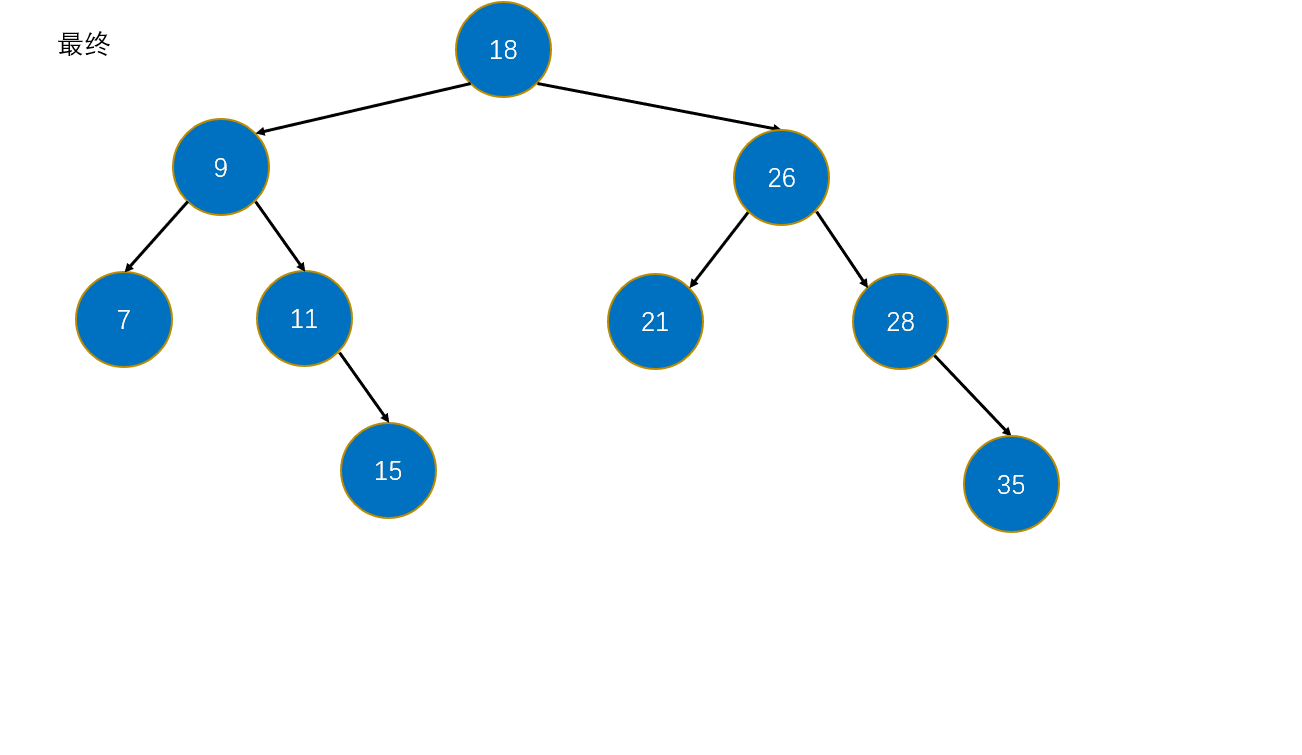
主要是要删除的节点有左右节点,因为对于这种情况,删除后还要去处理删除的节点的左右节点如何接上原树中。借助二叉搜索树的定义,我们可以找一个节点来做删除节点的左右子树的根节点,该节点的元素必须满足大于左子树中任意元素和小于右子树中任意元素。而且节点是要在这左右子树中找到,不是自己随便创个新的。如此一想,那么只能找到要删除的节点的右子树中的最小值。因为右子树的最小值满足:大于要删除的节点的左子树中的任意元素,并且也小于右子树的任意元素啊。这个可以画图试试。
(寻找的节点可称为要删除的节点的后驱节点,即要删除的节点的右子树中的最小值。其实,找到要删除的节点的左子树中的最大值也是可以的,称为前驱节点)
小结:要删除的节点有左右节点的删除步骤:
- 找到要删除的节点,记为d
- 在d的右子树中查找最小值,运用上面写的方法:minimin(d.right),并保存,记为s
- 那么此时要从d的右子树中删除最小值,运用上面写的方法:removeMin(d.right)
- 此时让s来替换掉d,即把d的左右子树都给s
- 最后返回以s为根的新树
(第一种写法:寻找的节点可称为要删除的节点的后驱节点,即要删除的节点的右子树中的最小值)
/**
* 删除任意元素
* @param e
*/
public void remove(E e) {
// 删除后会改变树结构,所以要更新原先的树
root = remove(root, e);
}
private Node remove(Node node, E e) {
if(node == null) {
return null;
}
// 当e小于根节点时,从左子树找
if(e.compareTo(node.e) < 0) {
// 可能改变左子树的结构
node.left = remove(node.left, e);
} else if(e.compareTo(node.e) > 0) { // 当e大于根节点时,从右子树找
node.right = remove(node.right, e);
} else { // 命中
// 删除只有右子树的节点的情况,不管右子树有没有,有也没影响
if(node.left == null) {
// 步骤跟删除最小值一样
Node rightNode = node.right;
node.right = null;
size--;
return rightNode;
}
// 删除只有左子树的节点的情况,不管左子树有没有
if(node.right == null) {
// 步骤跟删除最大值一样
Node leftNode = node.left;
node.left = null;
size--;
return leftNode;
}
// 对于有左右子树的节点
// 在要删除的节点的右子树中查询最小值
Node successor = minimun(node.right);
// 让要删除的节点的左右子树指向successor,,并移除右子树中的最小值
successor.left = node.left;
successor.right = removeMin(node.right);
// 注意小陷阱:此时还需要size--吗?想想,调用removeMin做了什么,删了一个节点,那么该方法会size--,虽然删除的不是我们要删除的节点
// 在删除后,我们可以先size++,当真正删除要删除的节点时,在size--。所以抵消了。
// 删除
node.left = null;
node.right = null;
return successor;
}
return node;
}
(第二种写法:找到要删除的节点的左子树中的最大值也是可以的,称为前驱节点)
private Node remove(Node node, E e) {
if(node == null) {
return null;
}
// 当e小于根节点时,从左子树找
if(e.compareTo(node.e) < 0) {
// 可能改变左子树的结构
node.left = remove(node.left, e);
} else if(e.compareTo(node.e) > 0) { // 当e大于根节点时,从右子树找
node.right = remove(node.right, e);
} else { // 命中
// 删除只有右子树的节点的情况,不管右子树有没有,有也没影响
if(node.left == null) {
// 步骤跟删除最小值一样
Node rightNode = node.right;
node.right = null;
size--;
return rightNode;
}
// 删除只有左子树的节点的情况,不管左子树有没有
if(node.right == null) {
// 步骤跟删除最大值一样
Node leftNode = node.left;
node.left = null;
size--;
return leftNode;
}
// 对于有左右子树的节点
// 在要删除的节点的左子树中查询最大值
Node predecessor = minimun(node.left);
// 让要删除的节点的左右子树指向predecessor,,并移除右子树中的最小值
predecessor.left = removeMax(node.left);
predecessor.right = node.right;
// 注意小陷阱:此时还需要size--吗?想想,调用removeMin做了什么,删了一个节点,那么该方法会size--,虽然删除的不是我们要删除的节点
// 在删除后,我们可以先size++,当真正删除要删除的节点时,在size--。所以抵消了。
// 删除
node.left = null;
node.right = null;
return predecessor;
}
return node;
}
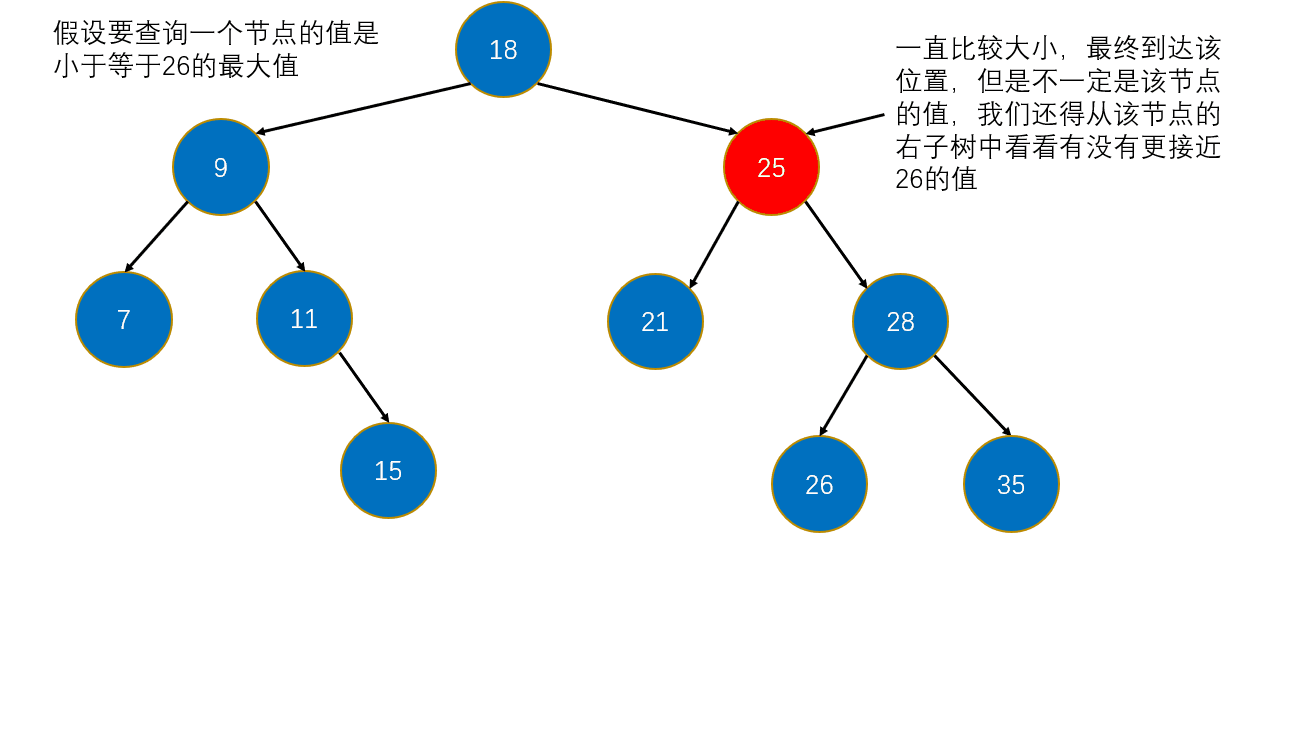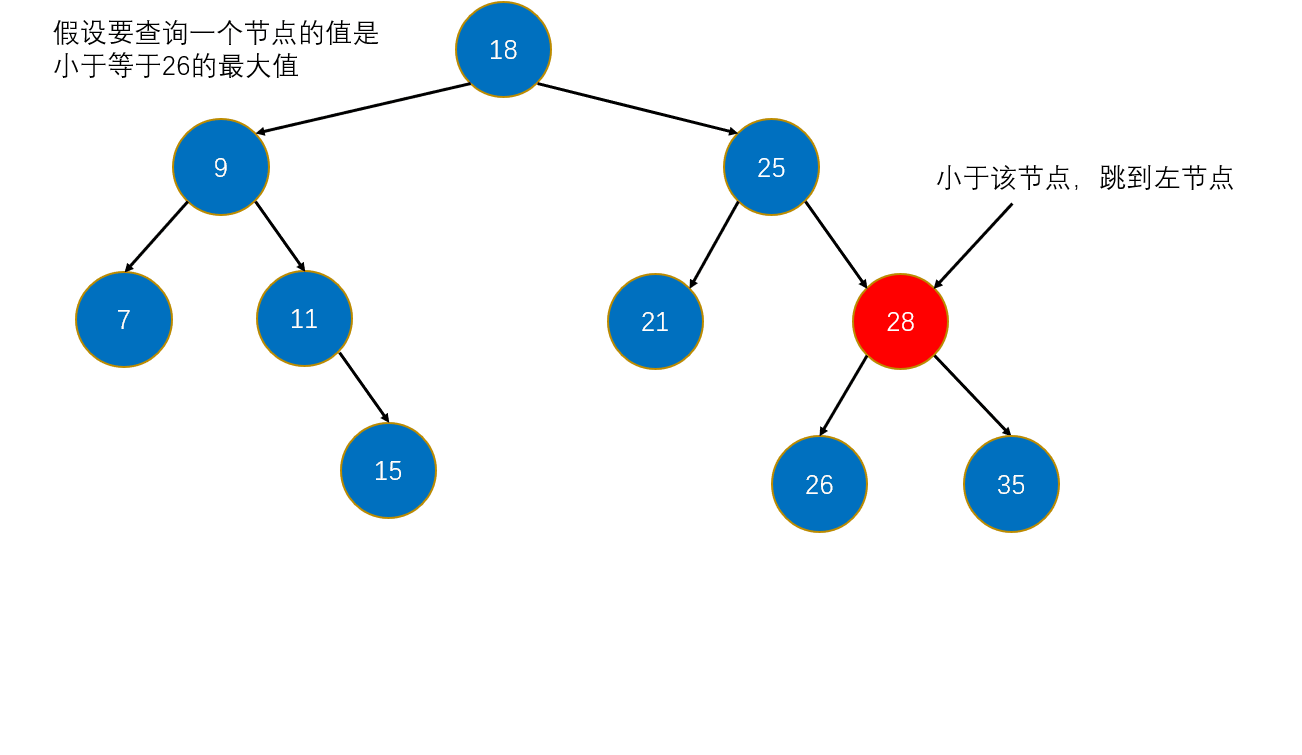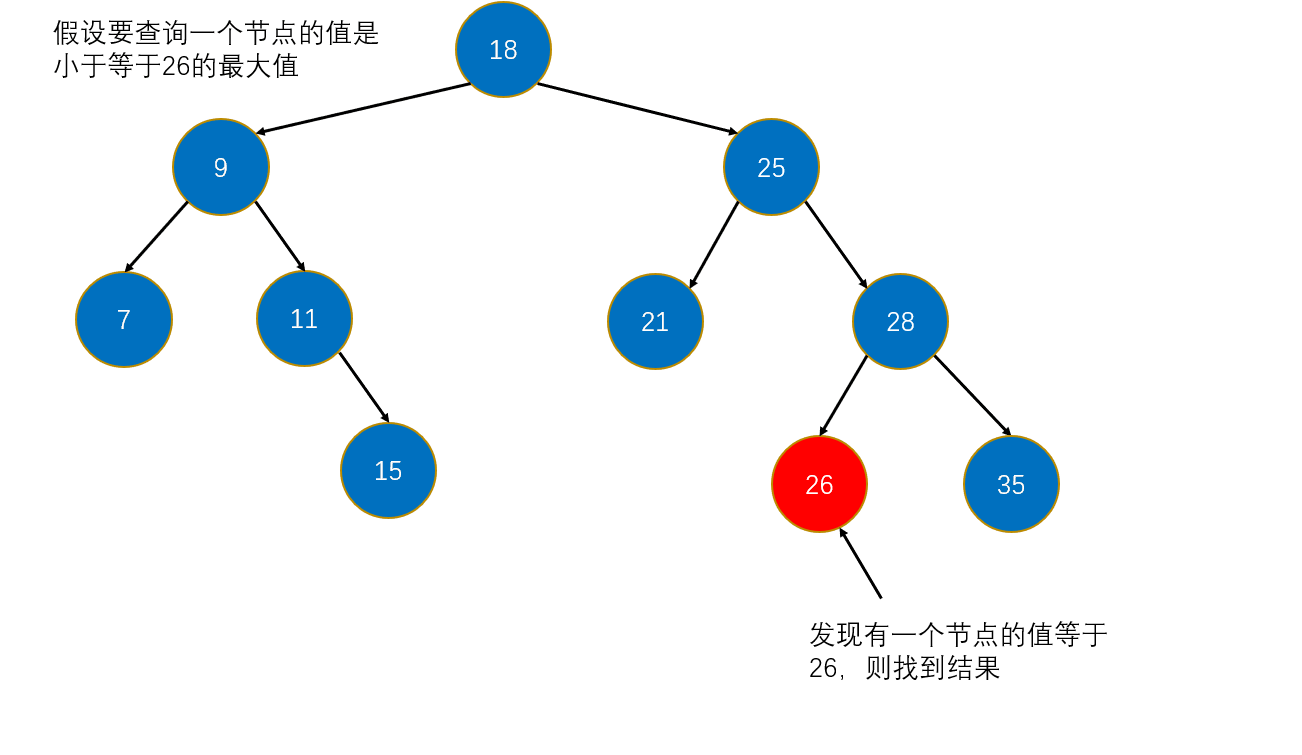
6. 向上取整(floor)和向下取整(ceil)
floor(e): 小于等于e的最大值,简单讲就是最接近于e且小于或等于e的值。
思路,有三种情况:
- 如果e等于根节点的值,那么直接返回;
- 如果e小于根节点的值,那么寻找的节点肯定在左子树中;
- 如果e大于根节点的值,那么寻找的节点可能根节点,也有可能在根节点的右子树中,所以还需要去根节点的右子树寻找。
/**
* 小于等于e的最大值(e可以不用在树中存在)
* 如果不存在返回null
* @param e
* @return
*/
public E floor(E e) {
Node node = floor(root, e);
return node != null ? node.e : null;
}
public Node floor(Node node, E e) {
if(node == null) {
return null;
}
// 如果等于根节点,则返回
if(e.compareTo(node.e) == 0) {
return node;
}
// 如果e小于根节点,则小于等于e的节点一定在根节点的左子树
if(e.compareTo(node.e) < 0) {
return floor(node.left, e);
}
// 否则,e大于根节点,那么要寻找的节点有可能就是当前的节点,也有可能在当前节点的右子树中
Node rightTree = floor(node.right, e);
if(rightTree != null) {
return rightTree;
} else {
// 找不到就返回根节点
return node;
}
}
图解:
ceil(e): 大于等于e的最大值,简单讲就是最接近于e且大于或等于e的值。
思路,有三种情况:
- 如果e等于根节点的值,那么直接返回;
- 如果e大于根节点的值,那么寻找的节点肯定在右子树中;
- 如果e小于根节点的值,那么寻找的节点可能根节点,也有可能在根节点的左子树中,所以还需要去根节点的左子树寻找。
/**
* 大于等于e的最小值(e可以不用在树中存在)
* 如果不存在返回null
* @param e
* @return
*/
public E ceil(E e) {
Node node = ceil(root, e);
return node != null ? node.e : null;
}
public Node ceil(Node node, E e) {
if(node == null) {
return null;
}
if(e.compareTo(node.e) == 0) {
return node;
}
// 如果e大于根节点,那么寻找的节点一定在右子树
if(e.compareTo(node.e) > 0) {
return ceil(node.right, e);
}
// 否则,e小于根节点,那么寻找的节点可能是根节点,也可能是在根节点的左子树中
Node leftNode = ceil(node.left, e);
if(leftNode != null) {
return leftNode;
} else {
return node;
}
}
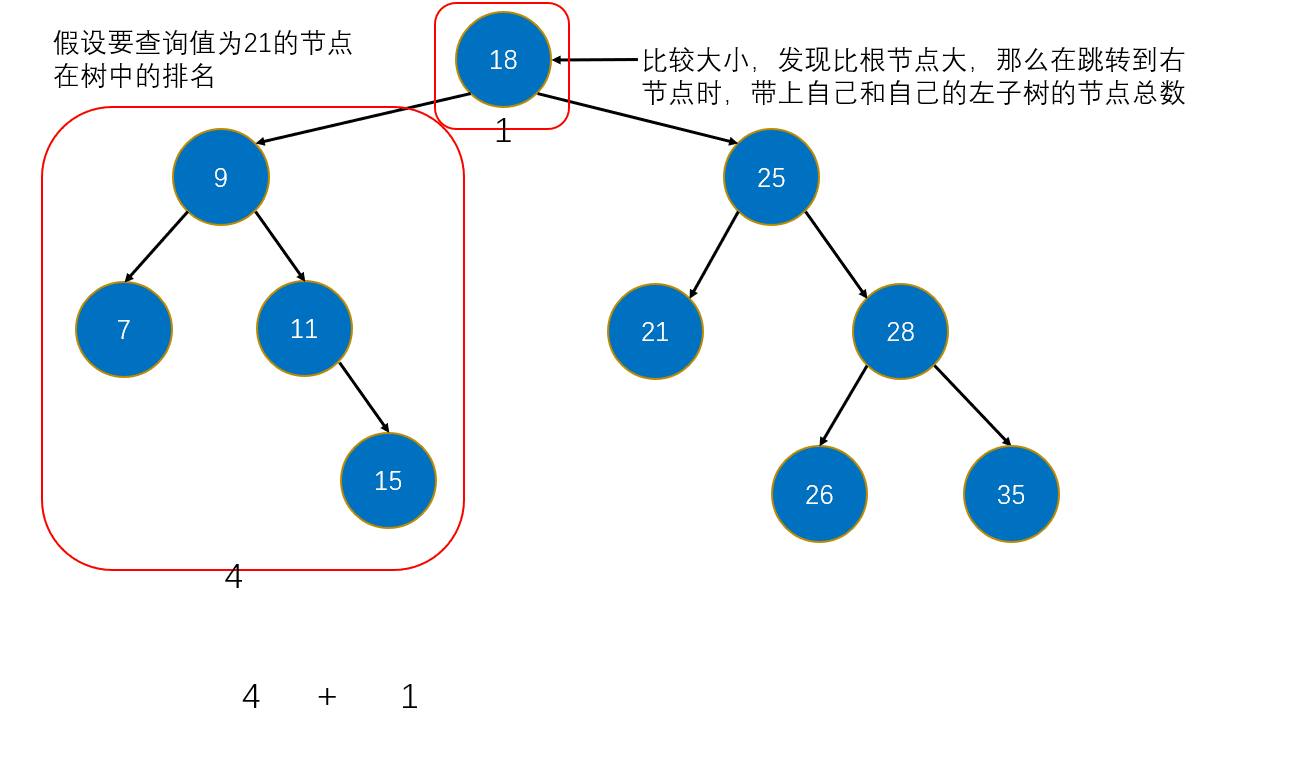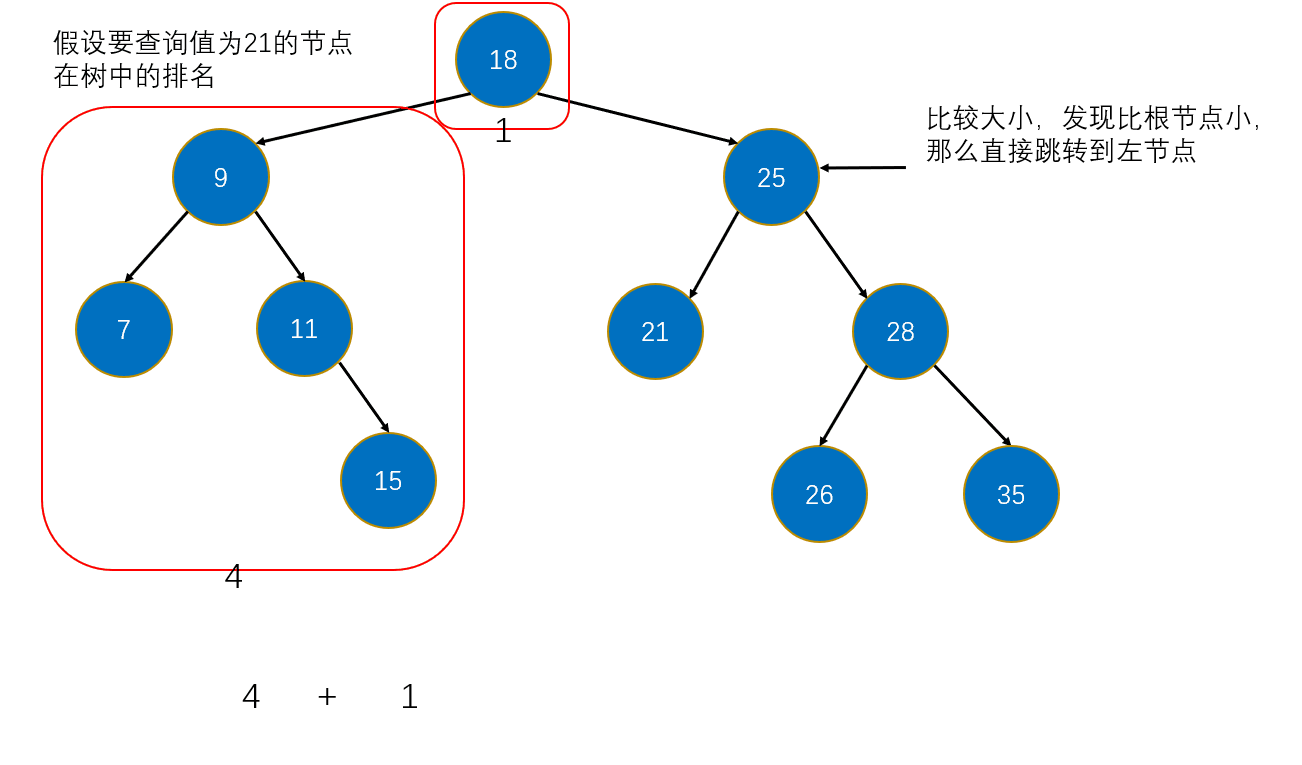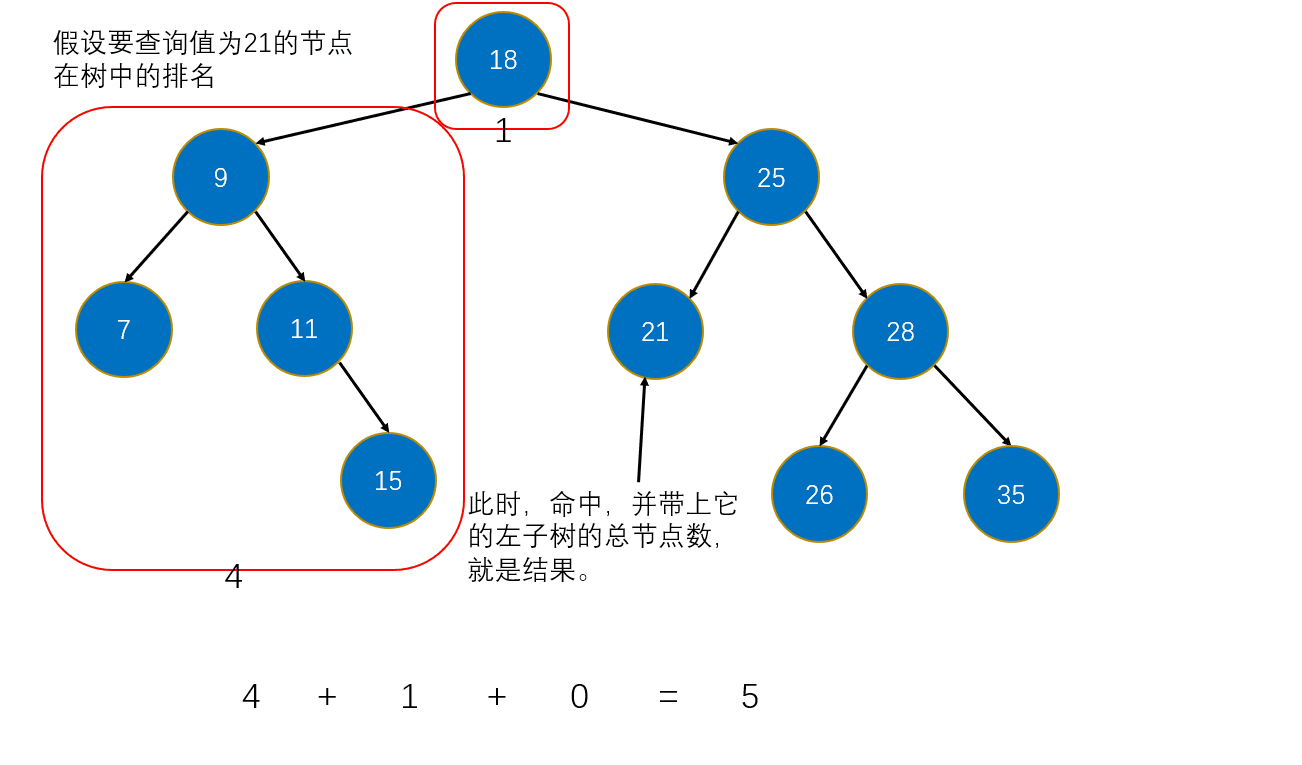
7. 排名(rank)
rank(e):e在树中的排名(小于e的元素的数量)。
思路:
- 如果e等于根节点元素,则返回:根节点的左子树的全部元素数量。
- 如果e小于根节点元素,则就跳到左子树中。
- 如果e大于根节点元素,那么需要跳到右子树中,并记录:根节点的左子树的全部元素数量 + 根节点。
/**
* e是排名第几元素
* @param e
* @return
*/
public int rank(E e) {
return rank(root, e);
}
private int rank(Node node, E e) {
if(node == null) {
return 0;
}
if(e.compareTo(node.e) == 0) {
return getNodeSize(node.left);
} else if(e.compareTo(node.e) < 0) {
return rank(node.left, e);
} else {
return rank(node.right, e) + 1 + getNodeSize(node.left);
}
}
/**
* 查询一棵树的节点数量
* @param node
* @return
*/
private int getNodeSize(Node node) {
if(node == null) {
return 0;
}
int leftSize = 0, rightSize = 0;
leftSize = getNodeSize(node.left);
rightSize = getNodeSize(node.right);
return leftSize + rightSize + 1;
}
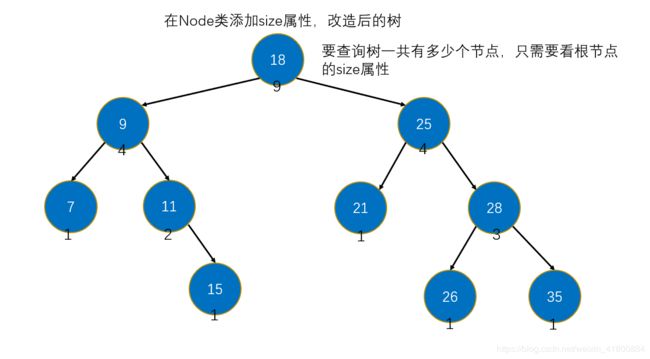
这是一种做法(不是很推荐使用,主要是还要去查节点数量),还有另一种做法,就是在Node类添加一个size的属性,该属性记录该节点的左右子树的节点数量加上自己。
相应的就需要去更改添加操作,维护每个节点的size属性。然后树中的size属性就可以不要了,因为节点已经维护了。
这个方法后续在搞,因为要改动的地方很多。
图解:
8. 选择(select)
select(e):找到排名为e的节点(即树中正好有e个小于该节点)。
后续也在搞,主要是跟键值对联合起来,通过键找值,现在树只是一个元素而已。
思路:跟排名方法的思路一样。
9. 使用BST实现Set集合
很容易:
public interface Set<E> {
void add(E e);
boolean isEmpty();
int getSize();
void remove(E e);
boolean contains(E e);
}
public class BSTSet<E extends Comparable<E>> implements Set<E> {
private BST<E> bst;
public BSTSet() {
this.bst = new BST<>();
}
@Override
public void add(E e) {
bst.add(e);
}
@Override
public boolean isEmpty() {
return bst.isEmpty();
}
@Override
public int getSize() {
return bst.getSize();
}
@Override
public void remove(E e) {
bst.remove(e);
}
@Override
public boolean contains(E e) {
return bst.contains(e);
}
}
10. 二叉搜索树的复杂度分析
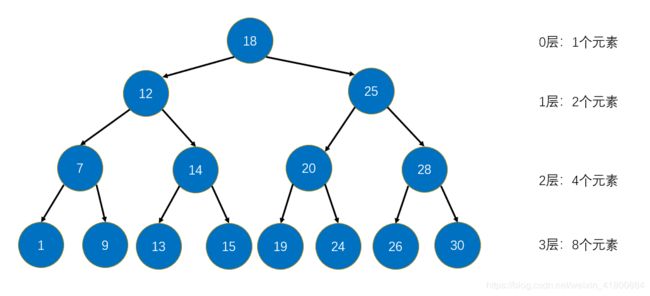
二叉搜索树中只有增删查三个操作。三个操作的时间复杂度都是一样的,因为每次都是去跟根节点比较,所以每比较一次就可以抛弃另一半子树,一直到叶子节点,可得这跟树的高度有关,设高度为h,那么时间复杂度为O(h)。
设n为元素个数,h跟n有什么关系?假设二叉树是一个满二叉树(即除叶子节点外的节点都有左右节点):
可以看出,对于第h层的元素个数有2^h。那么对于一颗满二叉树的元素个数总共有:
所以对于满二叉树的时间复杂度为O(logn),这只是平均的复杂度,因为二叉树不一定是满二叉树。
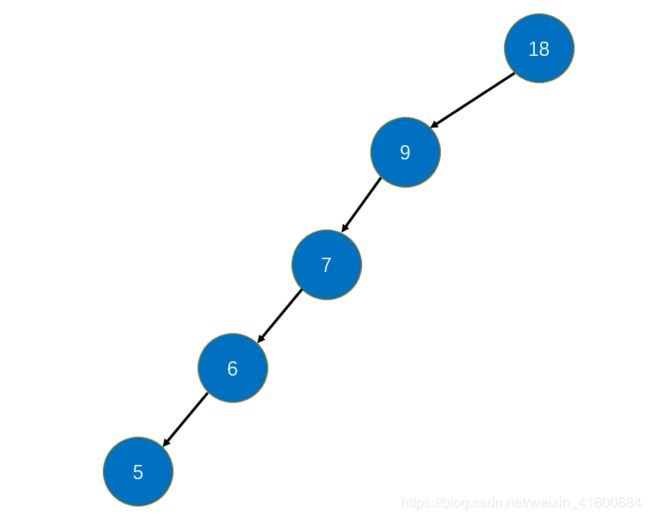
二叉树最坏的情况就是:
这种情况会退化成链表,即高度等于元素个数,最差时间复杂度为O(n)。可以发现,其实是因为顺序插入导致的原因。
后面有平衡二叉树来解决。
11. 使用二分搜索树实现Map
接口:
public interface Map<K, V> {
void add(K key, V value);
boolean isEmpty();
V remove(K key);
boolean containsKey(K key);
void set(K key, V newValue);
V get(K key);
int getSize();
}
实现:
public class BSTMap<K extends Comparable, V> implements Map<K, V> {
private class Node {
private K key;
private V value;
private Node left, right;
public Node(K key, V value) {
this.key = key;
this.value = value;
this.left = null;
this.right = null;
}
}
private Node root;
private int size;
public BSTMap() {
root = null;
size = 0;
}
/**
* 返回key所在的节点
* @param key
* @return
*/
private Node getNode(Node node, K key) {
if(node == null) {
return null;
}
if(key.compareTo(node.key) == 0) {
return node;
} else if(key.compareTo(node.key) < 0) {
return getNode(node.left, key);
} else {
return getNode(node.right, key);
}
}
/**
* 添加操作
* @param key 要添加的键
* @param value 要添加的值
*/
@Override
public void add(K key, V value) {
root = add(root, key, value);
}
private Node add(Node node, K key, V value) {
if(node == null) {
size++;
return new Node(key, value);
}
if(key.compareTo(node.key) < 0) {
// 如果是左子树,add返回新插入节点后的新左子树的根,那么替换掉旧树
node.left = add(node.left, key, value);
} else if(key.compareTo(node.key) > 0) {
// 如果是右子树,add返回新插入节点后的新右子树的根,那么替换掉旧树
node.right = add(node.right, key, value);
} else {
node.value = value;
}
// 返回根
return node;
}
/**
*
* @return 树是否为空
*/
@Override
public boolean isEmpty() {
return size == 0;
}
/**
* 查询键是否包含在树中
* @param key
* @return
*/
@Override
public boolean containsKey(K key) {
return getNode(root, key) != null;
}
/**
*
* @param key 要修改值的键
* @param newValue 新值
*/
@Override
public void set(K key, V newValue) {
Node node = getNode(root, key);
if(node == null) {
throw new IllegalArgumentException(key + " doesn't exist!");
}
node.value = newValue;
}
/**
*
* @param key
* @return 获取key的值
*/
@Override
public V get(K key) {
Node node = getNode(root, key);
return node != null ? node.value : null;
}
/**
*
* @return 树的大小
*/
@Override
public int getSize() {
return size;
}
/**
*
* @param key
* @return 移除以key的节点
*/
@Override
public V remove(K key) {
Node delNode = getNode(root, key);
if(delNode != null) {
root = remove(root, key);
return delNode.value;
}
return null;
}
/**
* 移除元素
* @param node
* @param key
* @return
*/
private Node remove(Node node, K key) {
if(node == null) {
return null;
}
if(key.compareTo(node.key) < 0) {
node.left = remove(node.left, key);
} else if(key.compareTo(node.key) > 0) {
node.right = remove(node.right, key);
} else {
if(node.left == null) {
Node rightNode = node.right;
node.right = null;
size--;
return rightNode;
}
if(node.right == null) {
Node leftNode = node.left;
node.left = null;
size--;
return leftNode;
}
// node.left != null && node.right != null
Node newNode = minimin(node.right);
// removeMin已经size--了
newNode.right = removeMin(node.right);
newNode.left = node.left;
node.left = null;
node.right = null;
return newNode;
}
return node;
}
/**
*
* @param node
* @return 要查询的最小值的节点
*/
private Node minimin(Node node) {
if(node.left == null) {
return node;
} else {
return minimin(node.left);
}
}
/**
*
* @param node
* @return 要移除的最小值的节点
*/
private Node removeMin(Node node) {
if(node.left == null) {
Node rightNode = node.right;
node.right = null;
size--;
return rightNode;
}
node.left = removeMin(node.left);
return node;
}
}
现在来修改一下,在Node类中添加size属性,并把Map中的size属性去掉:
public class BSTMap<K extends Comparable, V> implements Map<K, V> {
private class Node {
private K key;
private V value;
private Node left, right;
// 记录节点的左右子树的节点数加上当前节点的总数量
private int size;
public Node(K key, V value, int size) {
this.key = key;
this.value = value;
this.size = size;
this.left = null;
this.right = null;
}
}
private Node root;
public BSTMap() {
root = null;
}
/**
* 得到节点的左右子树的节点数加上当前节点的总数量
* @param node
* @return
*/
private int getSize(Node node) {
if(node == null) {
return 0;
} else {
return node.size;
}
}
/**
* 返回key所在的节点
* @param key
* @return
*/
private Node getNode(Node node, K key) {
if(node == null) {
return null;
}
if(key.compareTo(node.key) == 0) {
return node;
} else if(key.compareTo(node.key) < 0) {
return getNode(node.left, key);
} else {
return getNode(node.right, key);
}
}
/**
* 添加操作
* @param key 要添加的键
* @param value 要添加的值
*/
@Override
public void add(K key, V value) {
root = add(root, key, value);
}
/**
* 递归
* @param node
* @param key
* @param value
* @return
*/
private Node add(Node node, K key, V value) {
if(node == null) {
return new Node(key, value, 1);
}
if(key.compareTo(node.key) < 0) {
// 如果是左子树,add返回新插入节点后的新左子树的根,那么替换掉旧树
node.left = add(node.left, key, value);
} else if(key.compareTo(node.key) > 0) {
// 如果是右子树,add返回新插入节点后的新右子树的根,那么替换掉旧树
node.right = add(node.right, key, value);
} else {
node.value = value;
}
// 维护以node为根的节点总数
node.size = getSize(node.left) + getSize(node.right) + 1;
// 返回根
return node;
}
/**
*
* @return 树是否为空
*/
@Override
public boolean isEmpty() {
return root.size == 0;
}
/**
* 查询键是否包含在树中
* @param key
* @return
*/
@Override
public boolean containsKey(K key) {
return getNode(root, key) != null;
}
/**
*
* @param key 要修改值的键
* @param newValue 新值
*/
@Override
public void set(K key, V newValue) {
Node node = getNode(root, key);
if(node == null) {
throw new IllegalArgumentException(key + " doesn't exist!");
}
node.value = newValue;
}
/**
*
* @param key
* @return 获取key的值
*/
@Override
public V get(K key) {
Node node = getNode(root, key);
return node != null ? node.value : null;
}
/**
*
* @return 树的大小
*/
@Override
public int getSize() {
return root.size;
}
/**
*
* @param key
* @return 移除以key的节点
*/
@Override
public V remove(K key) {
Node delNode = getNode(root, key);
if(delNode != null) {
root = remove(root, key);
return delNode.value;
}
return null;
}
/**
* 移除元素
* @param node
* @param key
* @return
*/
private Node remove(Node node, K key) {
if(node == null) {
return null;
}
if(key.compareTo(node.key) < 0) {
node.left = remove(node.left, key);
} else if(key.compareTo(node.key) > 0) {
node.right = remove(node.right, key);
} else {
if(node.left == null) {
Node rightNode = node.right;
node.right = null;
return rightNode;
}
if(node.right == null) {
Node leftNode = node.left;
node.left = null;
return leftNode;
}
// node.left != null && node.right != null
Node newNode = minimin(node.right);
newNode.right = removeMin(node.right);
newNode.left = node.left;
node.left = null;
node.right = null;
return newNode;
}
node.size = getSize(node.left) + getSize(node.right) + 1;
return node;
}
/**
*
* @param node
* @return 要查询的最小值的节点
*/
private Node minimin(Node node) {
if(node.left == null) {
return node;
} else {
return minimin(node.left);
}
}
/**
*
* @param node
* @return 要移除的最小值的节点
*/
private Node removeMin(Node node) {
if(node.left == null) {
Node rightNode = node.right;
node.right = null;
return rightNode;
}
// 维护每个节点的子节点数
node.left = removeMin(node.left);
node.size = getSize(node.left) + getSize(node.right) + 1;
return node;
}
/**
* 排名
* @param key
* @return
*/
public int rank(K key) {
return rank(root, key);
}
private int rank(Node node, K key) {
if(node == null) {
return 0;
}
if(key.compareTo(node.key) == 0) {
return getSize(node.left);
} else if(key.compareTo(node.key) < 0) {
return rank(node.left, key);
} else {
return rank(node.right, key) + 1 + getSize(node.left);
}
}
/**
*
* @param rank
* @return 树中排名第几元素的键
*/
public K select(int rank) {
return select(root, rank).key;
}
private Node select(Node node, int rank) {
if(node == null) {
return null;
}
int leftSize = getSize(node.left);
if(leftSize > rank) {
return select(node.left, rank);
} else if(leftSize < rank) {
return select(node.right, rank-leftSize-1) ;
} else {
return node;
}
}
}
在Node添加了size,然后在add方法和remove方法添加:
node.size = getSize(node.left) + getSize(node.right) + 1;
该语句来维护每个节点的总节点数,我们使用的是递归写法,刚开始递(从上往下)时没有效果,因为此时树的结构还没改变,但归(从下往上),每个节点就会因为该语句而重新更新自己的总节点数。然后还实现了sank方法和select方法。
其他树结构待续。
参考:
慕课网liuyubobobo老师,突然发现网上好多教程都是参考他的,我也补充了liuyubobobo老师说的一些没有实现的方法,比如中序和后序的非递归写法,floor等。
推荐看《算法第四版》,树的知识讲得贼好。