机器学习经典算法之(十八) Linear Regression
一、线性回归简介:
在统计学中,线性回归(Linear Regression)是利用称为线性回归方程的最小平方函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析。这种函数是一个或多个称为回归系数的模型参数的线性组合。只有一个自变量的情况称为简单回归,大于一个自变量情况的叫做多元回归。
为了了解这个定义,我们先举个简单的例子:假设一个线性方程y=2x+30, x变量为体重(kg),y代表身高(cm),我们就能根据线性模型预测出 x =75时的身高;对于上面的简单的例子来说,我们可以粗略把 y =2x+30看成回归的模型;对于给予的每个人的体重都能预测出身高。
回归分析中,只包括一个自变量和一个因变量,且二者的关系可用一条直线近似表示,这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量,且因变量和自变量之间是线性关系,则称为多元线性回归分析。
线性回归是回归分析中第一种经过严格研究并在实际应用中广泛使用的类型。这是因为线性依赖于其未知参数的模型比非线性依赖于其位置参数的模型更容易拟合,而且产生的估计的统计特性也更容易确定。线性回归模型经常用最小二乘逼近来拟合,但他们也可能用别的方法来拟合,比如用最小化“拟合缺陷”在一些其他规范里(比如最小绝对误差回归),或者在桥回归中最小化最小二乘损失函数的惩罚.相反,最小二乘逼近可以用来拟合那些非线性的模型
二、线性回归实现原理(代码参考:《机器学习实战》):
import numpy as np
import matplotlib.pyplot as plt
#------------------------------------------------------------------------------
def loadDataSet(fileName):
numFeat=len(open(fileName).readline().split('\t'))-1
dataMat=[];labelMat=[]
fr=open(fileName)
for line in fr.readlines():
lineArr=[]
curLine=line.strip().split('\t')
for i in range(numFeat):
lineArr.append(float(curLine[i]))
dataMat.append(lineArr)
labelMat.append(float(curLine[-1]))
#print("dataMat=",dataMat,"type(dataMat)",type(dataMat))
#print("labelMat=",labelMat,"type(labelMat)",type(labelMat))
return dataMat,labelMat#返回样本行,特征列;labelMat是标签列。
def standRegres(xArr,yArr):
xMat=mat(xArr);yMat=mat(yArr).T
print("xMat=\n",xMat.shape,"yMat=\n",yMat.shape)
xTx=xMat.T*xMat
#2行100列数据*100行2列数据就是为了判断是否可逆。结果为:2行2列数据
if linalg.det(xTx)==0.0:
#求解对应的行列式值是否为0,如果为0,那么矩阵:不可逆。
print("This matrix issingular,cannot do inverse")
return
ws1=xTx.I*(xMat.T*yMat)
#xTx求逆矩阵;xMat.T*yMat为2行100列*100行1列=2行1列
ws2=(xTx.I*xMat.T)*yMat
ws3=linalg.solve(xTx,xMat.T*yMat)
print(ws1,ws2,ws3)
return ws1
deflwlr(testPoint,xArr,yArr,k=1.0):#加权线性回归。
xMat=mat(xArr);yMat=mat(yArr).T
m=shape(xMat)[0]
weights=mat(eye(m))
for j in range(m):
diffMat=testPoint-xMat[j,:]
weights[j,j]=exp(diffMat*diffMat.T/(-2.0*k**2))
xTx=xMat.T*(weights*xMat)
if linalg.det(xTx)==0.0:
print("This matrix issingular,cannot do inverse")
return
ws=xTx.I*(xMat.T*(weights*yMat))
return testPoint*ws
deflwlrTest(testArr,xArr,yArr,k=1.0):
m=shape(testArr)[0]
yHat=zeros(m)
for i in range(m):
yHat[i]=lwlr(testArr[i],xArr,yArr,k)
return yHat
def test2():
dataMat,labelMat=loadDataSet("d:\\ex0.txt")
ws=standRegres(dataMat,labelMat)
dataMat =mat(dataMat)
labelMat=mat(labelMat)
test(dataMat,labelMat,ws)
yHat=dataMat*ws#每一个样本都要和ws回归系数进行相乘计算结果。
print("corrcoef(yHat.T,labelMat)",corrcoef(yHat.T,labelMat)) #保证两个向量都是行向量。
三、sklearn中线性回归应用举例:
importnumpy as np
importmatplotlib.pyplot as plt
fromsklearn.datasets import load_boston
fromsklearn.linear_model import LinearRegression
boston =load_boston()
print(boston.keys())
print(boston.feature_names)
x =boston.data[:, np.newaxis, 5]
y =boston.target
lm =LinearRegression() #构建线性模型
lm.fit(x,y) #训练模型
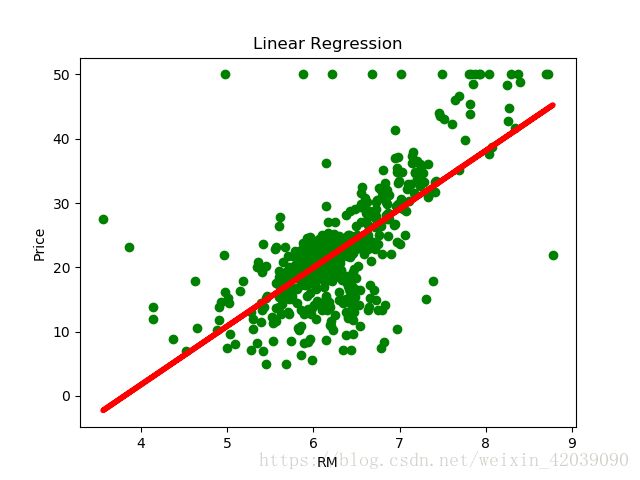
plt.scatter(x,y, color='green') #显示数据点
plt.plot(x,lm.predict(x), color='red', linewidth=4) #画出回归直线
plt.xlabel('RM')
plt.ylabel('Price')
plt.title('LinearRegression')
plt.show()
效果如下: