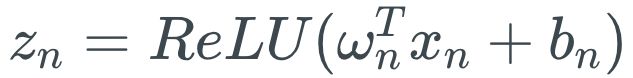深度学习 --- 优化入门三（梯度消失和激活函数ReLU）

前两篇的优化主要是针对梯度的存在的问题，如鞍点，局部最优，梯度悬崖这些问题的优化，本节将详细探讨梯度消失问题，梯度消失问题在BP的网络里详细的介绍过（兴趣有请的查看我的这篇文章），然后主要精力介绍RuLU激活函数，本篇还是根据国外的文章进行翻译，然后再此基础上补充，这样使大家更容易理解，好，那就开始了：

分布，该死的分布，还有统计学

不同于之前的机器学习方法，神经网络并不依赖关于输入数据的任何概率学或统计学假定。然而，为了确保神经网络学习良好，最重要的因素之一是传入神经网络层的数据需要具有特定的性质。

1. 数据分布应该是零中心化（zero centered）的，也就是说，分布的均值应该在零附近。不具有这一性质的数据可能导致梯度消失和训练动。

2. 最好分布的英文正态的，可能否则导致网络过拟合输入侧空间的某个区域。

3. 在训练过程中，不同批和不同网络层的激活分布，应该保持一定程度上的一致。如果不具备这一性质，那么我们说分布出现了内部协方差偏移（Internal Covariate shift），这可能拖慢训练进程。

这篇文章将讨论如何使用激活函数应对前两个问题。文末将给出一些选择激活函数的建议。

梯度消失

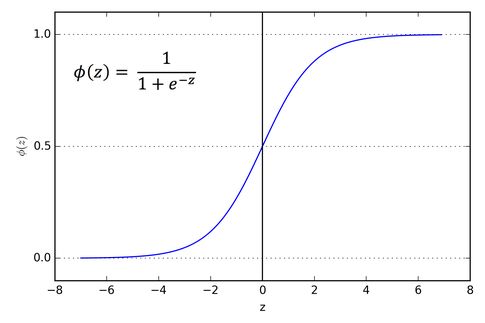
梯度消失问题在神经网络层数相对较多的时会遇到,,梯度消失原因是链式求导，导致梯度逐层递减，我们BP第一节推倒公式时就是通过链式求导把各层连接起来的，但是因为激活函数是SIGMOD函数，取值在1和-1之间，因此每次求导都会比原来小，当层次较多时，就会导致求导结果也就是梯度接近于0。具体如下所示：

        上图对应的神经网络的定义为，且  ，则表达式可为：

        又因为，因此最大值才为0.25，随着网络的加深,,总体的值越小，因此会发生梯度消失问题，一般解决方法是需要从激活函数或者网络层次着手，如激活函数考虑RELU函数代替SIGMOD函数。

与梯度消失相反的现象称为梯度爆炸，即反向传播中，每层都是大于1，导致最后累乘会很大，梯度爆炸容易解决，一般设定阈值就可以解决。

让我们做一个简单的试验。随机取样50个0到1之间的数，然后将它们相乘。  

import random

from functools import reduce

li = [random.uniform(0,1) for x in range(50)

print(reduce(lambda x,y: x*y, li))

你可以自己试验一下。我试了很多次，从来没能得到一个数量级大于10-18的数。如果这个值是神经元一个梯度的表达式中的一个因子，那么梯度几乎就等于零。这意味着，在较深的架构中，较深的神经元基本不学习，即使学习，和较浅的网络层中的神经元相比，学习的速率极低。

现象这个就是梯度消失问题，较深的神经元中的梯度变为零，或者说，消失了。这就导致神经网络中较深的层学习极为缓慢，或者，在最糟的情况下，根本不学习。

饱和神经元

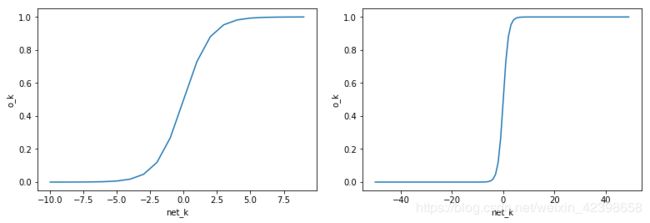
饱和神经元会导致梯度消失问题进一步恶化。假设，传入带sigmoid激活的神经元的激活前数值ωTx+ b非常大或非常小。那么，由于sigmoid在两端处的梯度几乎是0，任何梯度更新基本上都无法导致权重ω和偏置b发生变化，神经元的权重变动需要很多步才会发生。也就是说，即使梯度原本不低，由于饱和神经元的存在，最终梯度仍会趋向于零。如下图

                                                              

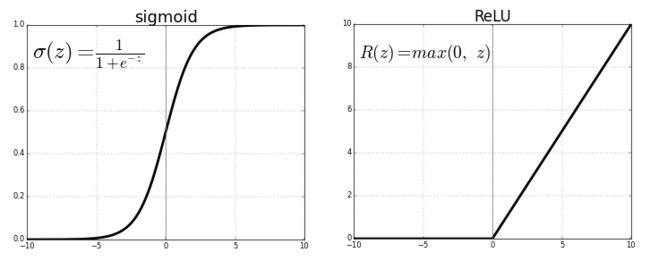
RELU救星

在普通深度网络设定下，RELU激活函数的引入是缓解梯度消失问题的首个尝试（LSTM的引入也是为了应对这一问题，不过它的应用场景是循环模型）。

当x> 0时，ReLU的梯度为1，x <0时，ReLU的梯度为0。这带来了一些好处.ReLU函数梯度乘积并不收敛于0，因为RELU的梯度要么是0，要么是1。当梯度值为1时，梯度原封不动地反向传播。当梯度值为0时，从这点往后不会进行反向传播。 

单边饱和

乙状结肠函数是双边饱和的，也就是说，正向趋于1，负向都趋向于零.ReLU则提供单边饱和。准确地说，RELU的左半部分不叫饱和，饱和的情况下，函数值变动极小，而RELU的左半部分根本不变。但两者的作用是类似的。你也许会问，单边饱和带来了什么好处？我们可以把深度网络中的神经元看成开关，这些开关专门负责检测特定特征。特征这些常常被称为概念。高层网络中的神经元也许最终会专门检测眼睛，轮胎之类的高层特征，而低层网络中的神经元最终专门检测曲线，边缘之类的低层特征。当这样的概念存在于神经网络的输入时，我们想要激活相应的神经元，而激活的数量级则可以测量概念的程度。例如，如果神经元检测到了边缘，它的数量级也许表示边缘的锐利程度。

                                                   由神经元创建的激活图学习不同的概念

然而，神经元的负值在这里就没什么意义了。用负值编码不存在的概念的程度感觉怪怪的。以检测边缘的神经元为例，相比激活值为5的神经元，激活值为10的神经元可能检测到了更锐利的边缘。但是区分激活值-5和-10的神经元就没什么意义了，因为负值表示根本不存在边缘。因此，用统一零表示概念不存在的英文很方便的.ReLU的单边饱和正符合这一点。

信息解缠和对噪声的鲁棒性

单边饱和提高了神经元对噪声的鲁棒性。为什么？假设神经元的值是无界的，也就是在两个方向上都不饱和。具有程度不同的概念的输入产生神经元正值输出的不同。由于我们想要用数量级指示信号的强度，这很好。然而，背景噪声，神经元不擅长检测的概念（例如，包含弧线的区域传入检测线条的神经元），会生成不同的神经元负值输出。这类不同可能给其他神经元带去大量无关，无用信息。这也可能导致单元间的相关性。例如，检测线条的神经元也许和检测弧线的神经元负相关。而在神经元单边饱和（负向）的场景下，噪声等造成的不同，也就是之前的负值输出数量级的不同，被激活函数的饱和元素挤压为零，从而防止噪声产生无关信号。

稀疏性

RELU函数在算力上也有优势。基于RELU的网络训练起来比较快，因为计算RELU激活的梯度不怎么需要算力，而乙状结肠梯度计算就需要指数运算.ReLU归零激活前的负值，这就隐式地给网络引入了稀疏性，同样节省了算力。

死亡RELU问题

RELU也有缺陷。虽然稀疏性在算力上有优势，但过多的稀疏性实际上会阻碍学习。激活前神经元通常也包含偏置项，如果偏置项是一个过小的负数，使得ωTx + b <0，那么ReLU激活在反向传播中的梯度就是0，使负的激活前神经元无法更新。如果学习到的权重和偏置使整个输入域上的激活前数值都是负数，那么神经元就无法学习，引起类似S形的饱和现象。称为这死亡RELU问题。

零中心化激活

不管输入是什么，RELU只输出非负激活。这可能是一个劣势。对基于RELU的神经网络而言，层网络的权重ωN的激活为

 因此，对损失函数大号而言：                                           

式上的中的英文一个指示函数，传入的RELU值为正数时输出1，否则输出0。由于RELU只输出非负值，ωN中的每项权重的梯度更新正负都一样。这里其实就是梯度了，RELU的特性的导数为1，并不影响误差的反向传播。 

这有什么问题？问题在于，由于所有神经元型态的梯度更新的符号都一样，网络层中的所有权重在一次更新中，要么全部增加，要么全部减少。然而，理想情况的梯度权重更新也许是某些权重增加，另一些权重减少.ReLU下，这做不到。假设，根据理想的权重更新，有些权重需要减少。然而，如果梯度更新是正值，这些权重可能在当前迭代中变为过大的正值。下一次迭代，梯度可能会变成较小的负值以补偿这些增加的权重，这也许会导致最终跳过需要少量负值或正值变动才能取到的权重。这可能导致搜寻时最小值出现字模式即会产生振荡，拖慢训练速度如下图所示：

Leaky ReLU和参数化ReLU

为了克服死亡ReLU问题，人们提出了Leaky ReLU（裂缝修正单元）.Leaky ReLU和普通ReLU几乎完全一样，除了x <0时有一个很小的斜率。在实践中，这个很小的斜率通常取0.01 ，Leaky ReLU的优势在于反向传播可以更新产生负的激活前值的权重，因为Leaky ReLU激活函数的负值区间的梯度是。因为负的激活值会生成负值而不是0，Leaky ReLU没有ReLU中的权重只在一个方向上更新的问题。该取多大，人们做了很多试验。有一种称为随机Leaky ReLU的方法，负值区间的斜率从均值为0，标准差为1的均匀分布中随机抽取如下：

 

原始论文提到随机的选取能得到比Leaky ReLU更好的结果，训练起来也更快，并通过经验方法得出，如果限定只使用单一的α值，那么1 / 5.5要比通常选择的0.01效果要好.Leaky ReLU奏效的原因是负值区间斜率的随机选择给负的激活前值梯度带来了随机性。在优化算法中引入的随机性，或者说噪声，有助于摆脱局部极小值和鞍点。后来人们又进一步提出，α可以看作一个参数，在网络的训练过程中学习。采用这一方法的激活函数称为参数化ReLU。

回顾下饱和

神经元饱和看起来是一件很糟的事情，但RELU中的单边饱和未必不好。尽管前面提到的一些RELU变体抑制了死亡RELU问题，但却丧失了单边饱和的益处。

指数线性单元和偏置偏移

基于上面的讨论，看起来一个完美的激活函数应该同时具备以下两个性质：

1. 产生零中心化分布，以加速训练过程。

2. 具有单边饱和，以导向更好的收敛。

Leaky ReLU和PReLU（参数化ReLU）满足第一个条件，不满足第二个条件。而原始的ReLU满足第二个条件，不满足第一个条件。

同时满足两个条件的一个激活函数是指数线性单元（ELU）。

                                                               

x> 0部分，ELU的梯度是1，x <0部分的梯度则是α×ex.ELU激活函数的负值区域趋向于-α。α是一个超参数，通常取1。

如何选择激活函数

1. 首先尝试RELU激活。尽管我们上面列出了RELU的一些问题，但很多人使用RELU取得了很好的结果。根据奥卡姆剃刀原则，先尝试更简单的方案比较好。相比RELU的有力挑战者，RELU的算力负担最轻。如果你的项目需要从头开始编程，那么RELU的实现也特别简单。

2. 如果ReLU的效果不好，我会接着尝试Leaky ReLU或ELU。我发现能够产生零中心化激活的函数一般要比不能做到这点的函数效果好得多.ELU看起来很有吸引力，但是由于负的激活前值会触发大量指数运算，基于ELU的网络训练和推理都很缓慢。如果算力资源对你而言不成问题，或者网络不是特别巨大，选择ELU，否则，选择Leaky ReLU .LReLU和ELU都增加了一个需要调整的超参数。

3. 如果算力资源很充沛，时间很充裕，你可以将上述激活函数的表现与PReLU和随机RELU做下对比。如果出现了过拟合，那么随机RELU可能会有用。参数化RELU加入了需要学习的一组参数，所以，只在具备大量训练数据的情况下才考虑选用参数化ReLU。

结语

这篇文章讨论了传入什么样的数据分布，有利于神经网络层恰当地学习。激活函数隐式地归一化这些分布，而一种称为批归一化（Batch Normalization）的技术明确地进行了这一操作。批归一化是近年来深度学习领域的主要突破之一。不过，我们要到本系列的下一篇文章才会讨论这一技术，目前而言，你可以亲自尝试下在自己的网络上使用不同的激活函数有什么效果！

 

进一步阅读

1. 爆炸梯度问题
2. 深入了解ReLU的优势
3. 关于是否仍在使用ReLU的reddit讨论，如果是，为什么？
4. ELU论文

 

原文网址：https：//blog.paperspace.com/vanishing-gradients-activation-function/（需要）

还需要添加点东西，一时想不到了，过段时间再来添加。