异常检测——Anomaly Detection

1.问题来源

概括：找和训练集不一样的数据。

2.应用

难点：异常点难以收集，无法穷举。我只能收集到正常情况的训练数据。

3.分类

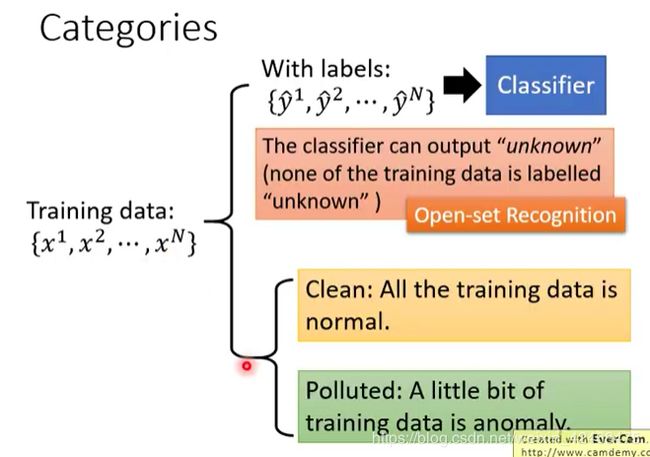
3.1 method1：With Classifier

不能被分类器 高置信地分类就当作异常点。
1.对每个非异常成员打标训练。

2.查看每一条数据 预测矢量 的最大值 c(x)，比较异常点和非异常点的c(x)值有没有明显的分界点。

但是总有一些异常点会被当作正常点

3.用 偏离集（dev set) 评估“异常检测”模型的 “异常阈值”λ ，要求偏离集有很多异常点和非异常点。

3.2 method 2：Gaussian distribution

这种情况下没有标签，从数据每一维特征的分布处理。

3.2.1 问题阐述

还是要寻找一个阈值，分布大于某一阈值为正常点，小于某一阈值为异常点。

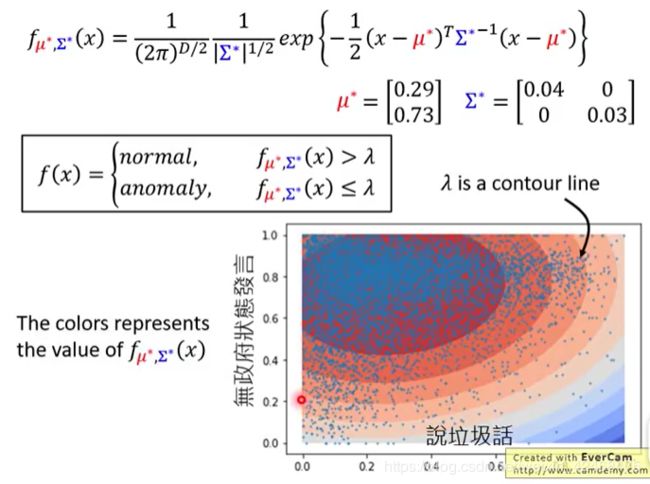
计算每一个样本的分布概率，累乘，寻找能让$L(\theta )$达到最大值的参数$\theta$。

$f_{\theta }(x)$具体展开：
实际上我们是要找 一组 $\mu$ 和 $\Sigma$，使得$L(\theta )$达到最大值。

为什么用高斯分布？ ：常见~

找到最佳参数后，把具体要检测的点带入，即可得到 f(x) 。D表述数据维度。

实现代码

1.首先要得到两个参数$\mu$ 和 $\Sigma$：

def getGaussianParams(X, useMultivariate):
    """
    The input X is the dataset with each n-dimensional data point in one row
    The output is an n-dimensional vector mu, the mean of the data set 
    the variances sigma^2, an n x 1 vector 或者是(n,n)矩阵，if你使用了多元高斯函数
    作业这里求样本方差除的是 m 而不是 m - 1，实际上效果差不了多少。
    """
    mu = X.mean(axis=0)
    if useMultivariate:    
        sigma2 = ((X-mu).T @ (X-mu)) / len(X)
    else:
        sigma2 = X.var(axis=0, ddof=0)  # 样本方差
    
    return mu, sigma2

2.计算每条数据的可能性

def gaussian(X, mu, sigma2):
    '''
    mu, sigma2参数已经决定了一个高斯分布模型
    因为原始模型就是多元高斯模型在sigma2上是对角矩阵而已，所以如下：
    If Sigma2 is a matrix, it is treated as the covariance matrix. 
    If Sigma2 is a vector, it is treated as the sigma^2 values of the variances
    in each dimension (a diagonal covariance matrix)
    output:
        一个(m, )维向量，包含每个样本的概率值。
    '''
# 如果想用矩阵相乘求解exp()中的项，一定要注意维度的变换。
# 事实上我们只需要取对角线上的元素即可。（类似于方差而不是想要协方差）
# 最后得到一个（m，）的向量，包含每个样本的概率，而不是想要一个（m,m）的矩阵
# 注意这里，当矩阵过大时，numpy矩阵相乘会出现内存错误。例如9万维的矩阵。所以画图时不能生成太多数据~！
#     n = len(mu) 
    
#     if np.ndim(sigma2) == 1:
#         sigma2 = np.diag(sigma2)

#     X = X - mu
#     p1 = np.power(2 * np.pi, -n/2)*np.sqrt(np.linalg.det(sigma2))
#     e = np.diag([email protected](sigma2)@X.T)  # 取对角元素，类似与方差，而不要协方差
#     p2 = np.exp(-.5*e)
    
#     return p1 * p2

# 下面是不利用矩阵的解法，相当于把每行数据输入进去，不会出现内存错误。
    m, n = X.shape
    if np.ndim(sigma2) == 1:
        sigma2 = np.diag(sigma2)

    norm = 1./(np.power((2*np.pi), n/2)*np.sqrt(np.linalg.det(sigma2)))
    exp = np.zeros((m,1))
    for row in range(m):
        xrow = X[row]
        exp[row] = np.exp(-0.5*((xrow-mu).T).dot(np.linalg.inv(sigma2)).dot(xrow-mu))
    return norm*exp

3.3 method 3: Auto-Encoder

只有正常的点会被较好地还原，异常点不会被很好地还原。

3.4 method 4: PCA

把多维数据（正常点+异常点）投影成低维，然后再把低维逆投影成原来的维度，正常点会和异常点还原的程度会不一样。

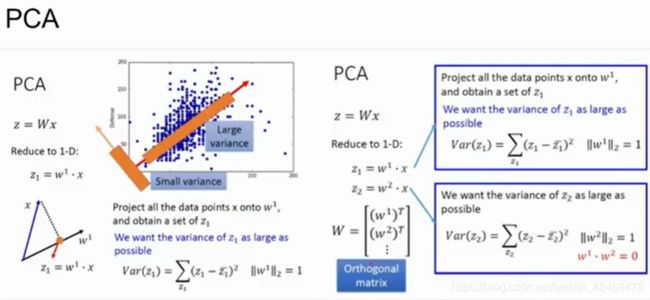
降到几维比较好？——用precision-recall曲线，这里来看是27比较好，因为阴影面积更加大，用roc曲线也可以判断~

3.5 method5：Isolation Forest

https://blog.csdn.net/bbbeoy/article/details/80300941?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522159179723219724843318563%2522%252C%2522scm%2522%253A%252220140713.130102334…%2522%257D&request_id=159179723219724843318563&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2_allsobaiduend~default-3-80300941.first_rank_ecpm_v3_pc_rank_v2&utm_term=%E5%BC%82%E5%B8%B8%E6%A3%80%E6%B5%8B%E7%AE%97%E6%B3%95

1. F. T. Liu, K. M. Ting and Z. H. Zhou，Isolation-based Anomaly Detection，TKDD，2011
   实现代码：
   https://scikit-learn.org/dev/modules/generated/sklearn.ensemble.IsolationForest.html

3.6 GAN anomaly detection

4.异常侦测系统（模型）的评价指标

自己定义

因为样本不平衡，所以不建议用accuracy，建议对照precision-recall表，比较假阳性和假阴性的重要程度，分别给予不同的权重，计算新的损失函数。

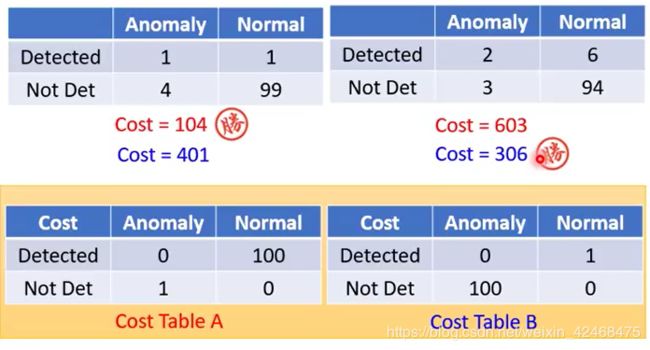
AUC

可以避免测试样本分布不平均的情况，使得假阳性和假阴性一样重要。

5.遇到检测错误的点

容易出现“意外”情况：

如何解决：
多找些异常点（通过generative model），让模型对异常点产出很低的置信度。