机器学习十大经典算法之决策树（学习笔记整理）

一、决策树概述

决策树是一种树形结构，其中每个内部节点表示一个属性上的测试，每个分支代表一个测试输出，每个叶节点代表一种类别。决策树是一个预测模型，代表的是对象属性与对象值之间的一种映射关系。

最初的节点称为根节点（如图中的"颜色"），有分支的节点称为中间节点（如图中的"价格"），无分支的节点称为叶节点（如图中的"喜欢"）

优点：计算复杂度不高，输出结果容易理解，对中间值的缺失不敏感，可以处理不相关特征数据
缺点：可能产生过拟合问题
适用数据类型：数值型和标称型

二、节点变量的选择

应该选择哪些变量作为根节点或中间节点生成决策树，目前主流的有三种方法。

1.ID3算法

(1) 信息的定义：
事件的不确定性越大，则其信息越多$$l(x_i)=-{\log }_{2}P(x_i)$$其中x_i是某一事件的第i个可能值，P(x_i)为其概率。
(2) 信息熵的定义：
信息熵为信息的数学期望$$H=-\sum _{k=1}^K{p}_k{\log }_2{p}_k$$某一事件有K个值，p_k表示第k个值发生的概率。
实际应用中可以用频率替换实际概率p_k$$H(D)=-\sum _{k=1}^K\frac{|C_k|}{|D|}{\log }_2\frac{|C_k|}{|D|}$$其中|D|表示事件中的所有样本点，|C_k|表示事件的第k个可能值出现的次数。
(3) 条件熵：
$$H(D|A)=\sum _{i,k}p(A_i)H(D_k|A_i)=-\sum _{i=1}^{n}P(A_i)\sum _{k=1}^{K}P(D_k|A_i){\log }_{2}P(D_k|A_i)$$其中P(A_i)为事件A第i种值对应的概率，P(D_k|A_i)为已知A_i的情况下D事件为第k种值的概率，即条件概率。
以频率代替概率：
$$H(D|A)=-\sum _{i=1}^n\frac{|D_i|}{|D|}\sum _{k=1}^K\frac{|D_{ik}|}{|D_i|}{\log }_2\frac{|D_{ik}|}{|D_i|}$$其中|D_i|为A_i的频数，|D_ik|为A_i下D事件为第k种值的频数。
(4) 信息增益：
$$Gai{n}_A(D)=H(D)-H(D|A)$$事件A对事件D的影响越大，则其条件熵H(D|A)就会越小，信息增益就越大。根节点或中间节点变量的选择，就是选择使因变量的信息增益最大的自变量。

2.C4.5算法

ID3算法信息增益会偏向于取值较多的变量，极端例子如果一个变量的取值正好是N个，则其条件熵会等于0，在该变量下因变量的信息增益一定是最大的，为了克服这种缺点，C4.5算法使用信息增益率对根节点或中间节点进行选择。
$$GainRati{o}_A(D)=\frac{Gai{n}_A(D)}{H_A}$$其中H_A为事件A的信息熵。时间A的取值越多，信息增益Gain_A(D)可能越大，但同时H_A也会越大，这样就以商的形式实现了对信息增益的惩罚。

3.CART算法

ID3和C4.5只能对离散型因变量进行分类，而CART可以处理连续型因变量。CART算法以基尼指数对根节点或中间节点进行选择。Python的sklearn模块使用的便是CART算法。
$$Gini=\sum _{k=1}^K{p}_k(1-p_k)=1-\sum _{k=1}^K{p}_k^2$$其中p_k为事件第k个可能值发生的概率。
以频率代替实际概率：$$Gini(D)=1-\sum _{k=1}^K(\frac{|C_k|}{|D|}{)}^2$$
条件基尼指数$$Gin{i}_A(D)=\sum _{i,k}P(A_i)Gini(D_k|A_i)=\sum _{i=1}^{2}P(A_i)(1-\sum _{k=1}^K{p}_{ik}^2)$$
$$Gin{i}_A(D)=\sum _{i=1}^2\frac{|D_i|}{|D|}(1-\sum _{k=1}^K(\frac{|D_{ik}|}{|D_i|}{)}^2)$$
$$\Delta Gini(D)=Gini(D)-Gin{i}_A(D)$$

三、决策树的剪枝

无论是用ID3、C4.5还是CART生成的决策树，都可能存在过拟合的问题，因此经常需要对决策树进行剪枝。

预剪枝

预剪枝是在树的生长过程中就对其进行必要的剪枝，如限制树的最大深度、限制中间节点和叶节点所包含的最小样本量、限制生成的最多叶节点数量等。

后剪枝

后剪枝是在树充分生长后再对其返工剪枝。

1.误差降低剪枝法(Reduced-Error Pruning, REP)

将某一非叶节点的子孙节点删除，使其变为新的叶节点。新叶节点的类别确定是利用该节点剪枝前包含的所有叶节点投票，频数最高的类别作为新的类别。利用测试集的数据对比剪枝前后的误判样本量，如果新树的误判样本量少于老树，则可以剪枝，否则不可剪枝。重复此步骤直到达到最大的预测准确率。由于使用测试集，该方法可能导致剪枝过度。

2.悲观剪枝法(Pessimistic Error Pruning, PEP)

自上向下的剪枝会增加误判率，因此对叶节点的误判个数增加一个经验性的惩罚系数0.5。
剪枝后的误判率：$$e^{\prime }(T)=(E(T)+0.5)/N$$剪枝前的误判率：$$e^{\prime }(T_t)=(\sum _{i=1}^{L}E(t_i)+0.5)/(\sum _{i=1}^L{N}_i)$$其中E(T)为中间节点T处的误判个数，N为中间节点T的样本个数，L为中间节点T下所有的叶节点个数，E(t_i)为中间节点T下所有叶节点的误判个数，N_i为各叶节点中的样本个数。
剪枝判断标准：
$$E(e^{\prime }(T))<E(e^{\prime }(T_t))+Std(e^{\prime }(T_t))$$其中E()是数学期望，Std()是标准差。

3.代价复杂度剪枝法(Cost-Complexity Pruning, CCP)

剪枝的代价是误判率会上升，但同时树的复杂度会减少，代价复杂度剪枝法引入了一个系数$\alpha$来平衡代价和复杂度。
代价复杂度剪枝法的目标函数：$$C_{\alpha }(T)=C(T)+\alpha \cdot |N_{leaf}|=\sum _{i=1}^L{N}_i\ast H(i)+\alpha \cdot |N_{leaf}|$$节点T下有L个叶节点，其中N_i为第i个叶节点的样本量，H(i)为第i个叶节点的信息熵，|N_leaf|=L。
剪枝前的目标函数：$C_{\alpha }(T{)}_{before}=C(T{)}_{before}+\alpha \cdot |N_{leaf}|$
剪枝后的目标函数：$C_{\alpha }(T{)}_{after}=C(T{)}_{after}+\alpha \cdot 1$
令$C_{\alpha }(T{)}_{before}=C_{\alpha }(T{)}_{after}$，得到：$$\alpha =\frac{C_{(}T{)}_{after}-C_{(}T{)}_{before}}{|N_{leaf}|-1}$$
循环计算$\alpha$值并减去$\alpha$值最小的节点，最终实现剪枝。
Python的sklearn中只提供了预剪枝的方法。

四、随机森林

如果预剪枝不够理想，还可以使用集成的随机森林算法，可以很好的避免单棵决策树过拟合的问题。
如果训练集有N个样本，P个自变量，1个因变量：

• 利用Bootstrap抽样法，从原始数据中生成k个数据集(样本个数N，变量个数P)
• 针对这k个数据集中的每一个数据集，构造一棵决策树(变量个数p，从总变量个数P中随机选择)，并且每一棵决策树都不剪枝。
• 针对这k棵决策树形成的随机森林，对分类问题利用投票法，得票最高的类别作为最终的判断结果；对回归问题利用均值法，所有结果的平均值作为最终的预测结果。
  在形成随机森林的过程中，由于每棵树的训练样本是随机的，构成树节点的变量也是随机选择的，所以使得随机森林不容易产生过拟合。

五、代码实现

首先仍然是所用到函数的官方文档解释
1.

(1)sklearn.tree.DecisionTreeClassifier(criterion=’gini’, splitter=’best’, max_depth=None, min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_features=None, random_state=None, max_leaf_nodes=None, min_impurity_decrease=0.0, min_impurity_split=None, class_weight=None, presort=False)
(2)sklearn.tree.DecisionTreeRegressor(criterion=’mse’, splitter=’best’, max_depth=None, min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_features=None, random_state=None, max_leaf_nodes=None, min_impurity_decrease=0.0, min_impurity_split=None, presort=False)

sklearn.ensemble.RandomForestClassifier(n_estimators=’warn’, criterion=’gini’, max_depth=None, min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_features=’auto’, max_leaf_nodes=None, min_impurity_decrease=0.0, min_impurity_split=None, bootstrap=True, oob_score=False, n_jobs=None, random_state=None, verbose=0, warm_start=False, class_weight=None)

sklearn.ensemble.RandomForestRegressor(n_estimators=’warn’, criterion=’mse’, max_depth=None, min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_features=’auto’, max_leaf_nodes=None, min_impurity_decrease=0.0, min_impurity_split=None, bootstrap=True, oob_score=False, n_jobs=None, random_state=None, verbose=0, warm_start=False)

接下来是代码

1.分类

import pandas as pd
import numpy as np
from sklearn import model_selection,tree,metrics,ensemble
from sklearn.model_selection import GridSearchCV
import matplotlib.pyplot as plt

data=pd.read_csv(r'C:\Users\Administrator\Desktop\data.csv')
#拆分训练集和测试集
predictors=data.columns[1:]
x_train,x_test,y_train,y_test=model_selection.train_test_split(data[predictors],data.Survived,
                                                               test_size=0.25,random_state=1234)

#使用网格搜索法，尝试不同组合（最大深度、分支最小样本量、叶节点最小样本量）
#根据经验，数据量较小时树的最大深度可设置10以内，较大时则需设置比较大的树深度，如20左右
max_depth=[2,3,4,5,6]
min_samples_split=[2,4,6,8]
min_samples_leaf=[2,4,8,10,12]
parameters={'max_depth':max_depth,'min_samples_split':min_samples_split,'min_samples_leaf':min_samples_leaf}
#网格搜索法，测试不同的参数值
grid_dtcateg=GridSearchCV(estimator=tree.DecisionTreeClassifier(),param_grid=parameters,cv=10)
#模型拟合
grid_dtcateg.fit(x_train,y_train)
#返回最佳参数组合
print(grid_dtcateg.best_params_)

#构建分类决策树
CART_Class=tree.DecisionTreeClassifier(max_depth=grid_dtcateg.best_params_['max_depth'],
                                       min_samples_leaf=grid_dtcateg.best_params_['min_samples_leaf'],
                                       min_samples_split=grid_dtcateg.best_params_['min_samples_split'])
decision_tree=CART_Class.fit(x_train,y_train)
pred=CART_Class.predict(x_test)
print('测试集的预测准确率：',metrics.accuracy_score(y_test,pred))
print('训练集的预测准确率：',metrics.accuracy_score(y_train,CART_Class.predict(x_train)))

#绘制ROC曲线
y_score=CART_Class.predict_proba(x_test)[:,1] #预测值为第2种的概率
fpr,tpr,threshold=metrics.roc_curve(y_test,y_score)
#计算AUC的值
roc_auc=metrics.auc(fpr,tpr)
#绘制面积图
plt.stackplot(fpr,tpr,color='steelblue',alpha=0.5,edgecolor='black')
#添加边际线和对角线
plt.plot(fpr,tpr,color='black',lw=1)
plt.plot([0,1],[0,1],color='red',linestyle='--')
#添加文本信息
plt.text(0.4,0.4,'DecisionTree ROC curve (area = %0.2f)' % roc_auc)
#添加x轴和y轴标签
plt.xlabel('l-Specificity')
plt.ylabel('Sensitivity')
plt.show()

#构建随机森林
RF_class=ensemble.RandomForestClassifier(n_estimators=200,random_state=1234)
RF_class.fit(x_train,y_train)
RFclass_pred=RF_class.predict(x_test)
print('随机森林模型在测试集的预测准确率：',metrics.accuracy_score(y_test,RFclass_pred))

#绘制ROC曲线
y_score=RF_class.predict_proba(x_test)[:,1]
fpr,tpr,threshold=metrics.roc_curve(y_test,y_score)
#计算AUC的值
roc_auc=metrics.auc(fpr,tpr)
#绘制面积图
plt.stackplot(fpr,tpr,color='steelblue',alpha=0.5,edgecolor='black')
#添加边际线和对角线
plt.plot(fpr,tpr,color='black',lw=1)
plt.plot([0,1],[0,1],color='red',linestyle='--')
#添加文本信息
plt.text(0.4,0.3,'RandomForest ROC curve (area = %0.2f)' % roc_auc)
#添加x轴和y轴标签
plt.xlabel('l-Specificity')
plt.ylabel('Sensitivity')
plt.show()

#变量重要程度绘图
importance=RF_class.feature_importances_
Impt_Series=pd.Series(importance,index=x_train.columns)
Impt_Series.sort_values(ascending=True).plot('barh')
plt.show()

结果：

可以看到使用随机森林确实提高了准确率

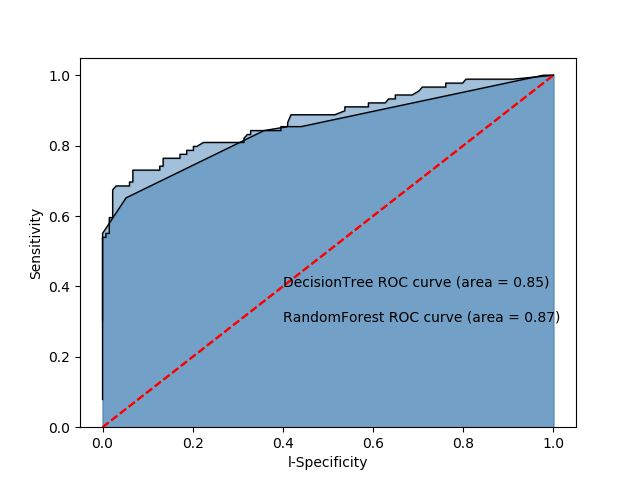
ROC曲线下的面积AUC均超过0.8，可以认为模型拟合效果比较理想，并且随机森林的ROC曲线AUC更大。

变量重要性程度如下：

2.预测

import pandas as pd
from sklearn import model_selection,tree,metrics,ensemble
from sklearn.model_selection import GridSearchCV

data=pd.read_excel(r'C:\Users\sc\Desktop\NHANES.xlsx')
#拆分训练集和测试集
predictors=data.columns[:-1]
x_train,x_test,y_train,y_test=model_selection.train_test_split(data[predictors],data.CKD_epi_eGFR,
                                                               test_size=0.25,random_state=1234)
#预设各参数
max_depth=[18,19,20,21,22]
min_samples_split=[2,4,6,8]
min_samples_leaf=[2,4,8,10,12]
parameters={'max_depth':max_depth,'min_samples_split':min_samples_split,'min_samples_leaf':min_samples_leaf}
#网格搜索法，测试不同的参数值
grid_dtcateg=GridSearchCV(estimator=tree.DecisionTreeRegressor(),param_grid=parameters,cv=10)
grid_dtcateg.fit(x_train,y_train)
#返回最佳参数组合
print(grid_dtcateg.best_params_)

#构建回归的决策树
CART_Reg=tree.DecisionTreeRegressor(max_depth=grid_dtcateg.best_params_['max_depth'],
                                    min_samples_leaf=grid_dtcateg.best_params_['min_samples_leaf'],
                                    min_samples_split=grid_dtcateg.best_params_['min_samples_split'])
CART_Reg.fit(x_train,y_train)
pred=CART_Reg.predict(x_test)
print('决策树均方误差MSE：',metrics.mean_squared_error(y_test,pred))

#构建用于回归的随机森林
RF=ensemble.RandomForestRegressor(n_estimators=200,random_state=1234)
RF.fit(x_train,y_train)
RF_pred=RF.predict(x_test)
print('随机森林均方误差：',metrics.mean_squared_error(y_test,RF_pred))

结果：

可以看到随机森林模型的均方误差要小很多。

参考文献：
[1]scikit-learn官方文档：http://scikit-learn.org/stable/index.html
[2]Peter Harrington.《机器学习实战》.人民邮电出版社,2013-6
[3]刘顺祥.《从零开始学Python数据分析与挖掘》.清华大学出版社,2018