第十届蓝桥杯C/C++B组试题水题解析

这一届蓝桥杯本人没参加，近期才看到题目，拿到的时候就仔细瞅了瞅，敲了会儿代码，没想到几个小时之内就搞定了其中百分之80的题目，我等智商只处于标准线下游的菜鸡都能达到的水准，大家又何尝不能呢？因此，废话不多说，接下来就带大家探究一番这次比赛中的水题吧~

1、填空题

试题 A: 组队

本题总分：5 分
【问题描述】
作为篮球队教练，你需要从以下名单中选出 1 号位至 5 号位各一名球员，
组成球队的首发阵容。
每位球员担任 1 号位至 5 号位时的评分如下表所示。请你计算首发阵容 1
号位至 5 号位的评分之和最大可能是多少？

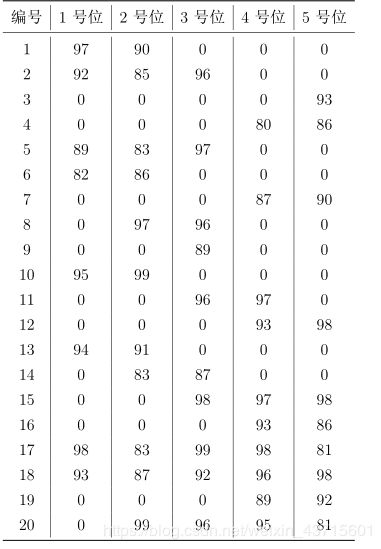
解析：每次比赛的第一道填空题都算是最简单的题目了吧？但往往最简单的题目，就可能会被出题人设下最明显却最容易让人掉入的陷阱，所以大家做这一道题的时候也需要谨慎一些。

这道题对于喜欢篮球的同学可能会敏感一些，我们都知道，一个优秀的球员可以往往可以胜任很多位置，如中锋，后卫等等，但教练却一般会安排这个优秀的球员打他得分最好或最稳定的位置。因而，题中教练挑选某个号位的球员一般来说是该号位上发挥最佳的球员，但是，请注意，一个球员只能胜任一个位置，所以，最佳方案应该为以下任意一种：

试题 B: 年号字串

本题总分：5 分
【问题描述】
小明用字母 A 对应数字 1，B 对应 2，以此类推，用 Z 对应 26。对于 27以上的数字，小明用两位或更长位的字符串来对应，例如 AA 对应 27，AB 对应 28，AZ 对应 52，LQ 对应 329。
请问 2019 对应的字符串是什么？

解析：这题拿到之后先别急着用编程解题，本人提倡对于比赛或者考试能够用最简单的方法解题就尽量用最简单的方法，这样才能够在有限的时间内腾出更多的世界来去思索后面的那些难度比较大的题目。

这道题对于精通进制转换的同学来说无异于是一道福音的送分题了，由题意我们可知，A对应数字1，B对应2，以此类推，Z对于26，而27以上的数字如AA对应27…如此规律且整齐，这难道不就是一道有关于26进制数的转换问题吗？但是与26进制数略有不同，它是从1开始的，并不是从0开始，所以，如题中所说的AA对应的十进制数的为1 × 26 ^ 1 + 1 × 26 ^ 0 = 27,AB对应的十进制数的为1 × 26 ^ 1 + 2 × 26 ^ 0 = 28,AZ对应的十进制数的为1 × 26 ^ 1 + 26 × 26 ^ 0 = 52,LQ对应的十进制数的为12 × 26 ^ 1 + 17 × 26 ^ 0 = 329…

同理，2019 = 2 × 26 ^ 2 + 25 × 26 ^ 1 + 17 × 26 ^ 0,对应的字符串即BYQ

(针对于本题而言,数据较小，口算或稍加计算便可得出，若数据过大时请采用除26取余法，如2019 / 26 = 77,2019 % 26 = 17，对应Q,77 / 26 = 2, 77 % 26 = 25,对应Y，2 / 26 = 0, 2 % 26 = 2,对应B，即BYQ)

试题 C: 数列求值

本题总分：10 分
【问题描述】
给定数列 1, 1, 1, 3, 5, 9, 17, …，从第 4 项开始，每项都是前 3 项的和。求第 20190324 项的最后 4 位数字。

解析：对于这道题,想必是广大刷题党的福音了吧,这就是很简单的一道类似于求斐波那契数列数列第n项的题目，但这里有一个问题就是，当n较大时，得出的结果对于计算机可能无法表示出来，对于一个32位的计算机，若它用我们熟悉的IEEE 754标准，能够表示的最大浮点数也只为2 ^ 127 × (2 - 2^-23),而斐波那契数列的第1000项便达到了惊人的4.3 × 10 ^ 208了,对于我们目前常用的计算机而言，还没有哪种计算机有数据类型可以表示这么大的数。

因而，题目一般来说都不会过于刁钻，让你去求斐波那契数列的某某很大一个数的项，只会让你去求该项的后几位数。

所以，我们要解决的问题就简单多了，就是求题中所给带有规律性数列的第n项的后四位数，思路很简单，就是设置4个变量f1,f2,f3,f，分别记录数列的第n - 3项,第n - 2项,第n - 1项,第n项的值，初始时f1 = f2 = f3 = 1,当n >=4 时每次计算时令 f = (f1 + f2 + f3) % 10000,计算后令f1 = f2 % 10000, f2 = f3 % 10000; f3 = f %10000; 并计算 n - 3次即可。

#include<iostream>
using namespace std;
int main(){
	long long f1 = 1, f2 = 1, f3 = 1;
	long long f = 0;
	for(long long i = 0;i <= 20190320;i++){
	f = (f1 + f2 + f3) % 10000;
	f1 = f2 % 10000;
	f2 = f3 % 10000;
	f3 = sum % 10000;
    }
	cout << f << endl;
}

最终答案为4659,注意最好不要使用数组，因为操作系统规定的用户内存区可不会随便让你拿近一个G的内存空间做实验…

试题 D: 数的分解

本题总分：10 分
【问题描述】
把 2019 分解成 3 个各不相同的正整数之和，并且要求每个正整数都不包含数字 2 和 4，一共有多少种不同的分解方法？
注意交换 3 个整数的顺序被视为同一种方法，例如 1000+1001+18 和
1001+1000+18 被视为同一种。

解析:考虑将1个数分解成3个正整数时,我们不妨用动态规划的思想先考虑一下将1个数分解成2个正整数的情况，就拿5来举例子吧，5 = 1 + 4 = 2 + 3 = 3 + 2 = 4 + 1，不考虑数的顺序的话，有 4种情况，而考虑数的顺序的话，只有 5 / 2 = 2种情况,再比如6 = 1 + 5 = 2 + 4 = 3 + 3 = 4 + 2 = 5 + 1，不考虑数的顺序的话，有5种情况，而考虑数的顺序的话，只有 6 / 2 = 3种情况…

将上述规律推广到正整数n时，可以发现,当n >= 2时,不考虑数的顺序的话，有n - 1种分解情况，考虑数的分解情况的话，仅有n / 2种情况。

再看1个数分解成3个正整数时的情况，比如将6分解成1、2、3这3个正整数，如果不考虑数的分解顺序的话,一共有如下 6 = 1 + 2 + 3 = 1 + 3 +2 = 2 + 1 + 3 = 2 + 3 + 1 = 3 + 1 + 2 = 3 + 2 + 1 (A33 = 3 × 2 × 1) 共6种情况。而考虑数的顺序的话，仅有1种情况,而如果从这6种不考虑数的顺序情况里挑选一种情况来代表这1种考虑数的顺序的情况，我们一般都会选6 = 1 + 2 + 3（三个正整数升序排列）或 6 = 3 + 2 + 1（三个正整数降序排列）这两种情况。

这里我采用的是三个正整数升序排列的情况，因而使得这三个正整数不相同。而1个数分解成3个正整数，可降解为1个数分解成2个正整数的情况，如12 = 1 + (11) = 1 + (2 + 9) = 3 + (9) = 3 + (4 +5) ,即第一个正整数满足变化范围1 ~ n/2,第2个正整数和第三个正整数之和满足变化范围1 ~ n/2,再除去每个数不含2和4的情况即可。

#include<iostream>
using namespace std;
int check(int temp){
	while(temp){		
		int r = temp % 10;
		if(r == 2 || r ==4) return 1; 
		temp /= 10;
	}
	return 0;
}
int f(int n,int k){
	int count = 0;
	for(int i = k + 1; i < n/2; i++){
		int a = i;
		int b = n - a - k;
		if(check(a) || check(b) || a >= b) continue;
		count++;
	}
	return count;
	
}
int division(int n){
	int sum = 0;
	for(int i = 1;i < n/2;i++){
         if(check(i)) continue;
		sum += f(n,i);
	}
	return sum;
} 
int main(){
		cout << division(2019) << endl;
}

最终计算答案为40785

2、编程题

试题 F: 特别数的和

时间限制: 1.0s 内存限制: 256.0MB 本题总分：15 分

【问题描述】
小明对数位中含有 2、0、1、9 的数字很感兴趣（不包括前导 0），在 1 到
40 中这样的数包括 1、2、9、10 至 32、39 和 40，共 28 个，他们的和是 574。
请问，在 1 到 n 中，所有这样的数的和是多少？

【输入格式】
输入一行包含两个整数 n。

【输出格式】
输出一行，包含一个整数，表示满足条件的数的和。

【样例输入】
40

【样例输出】
574

【评测用例规模与约定】
对于 20% 的评测用例，1 ≤ n ≤ 10。
对于 50% 的评测用例，1 ≤ n ≤ 100。
对于 80% 的评测用例，1 ≤ n ≤ 1000。
对于所有评测用例，1 ≤ n ≤ 10000。

解析:这道题就没有什么好说的了吧…妥妥的一道水题，直接安排代码吧…

#include<iostream>
using namespace std;
int check(int temp){
	while(temp){		
		int r = temp % 10;
		if(r == 2 || r ==0 || r == 1 || r == 9) return 1; 
		temp /= 10;
	}
	return 0;
}
int main(){
	int n;
	cin >> n;
	int sum = 0;
	for(int i = 1;i <= n;i++){
		if(check(i)) sum += i;
	} 
	cout << sum <<endl;
}

试题 G: 完全二叉树的权值

时间限制: 1.0s 内存限制: 256.0MB 本题总分：20 分

【问题描述】
给定一棵包含 N 个节点的完全二叉树，树上每个节点都有一个权值，按从上到下、从左到右的顺序依次是 A 1 , A 2 , ··· A N ，如下图所示：

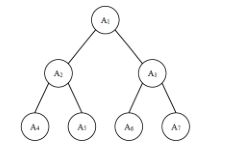
现在小明要把相同深度的节点的权值加在一起，他想知道哪个深度的节点权值之和最大？如果有多个深度的权值和同为最大，请你输出其中最小的深度。
注：根的深度是 1。

【输入格式】
第一行包含一个整数 N。
第二行包含 N 个整数 A 1 , A 2 , ··· A N 。

【输出格式】
输出一个整数代表答案。

【样例输入】
7
1 6 5 4 3 2 1

【样例输出】
2

【评测用例规模与约定】
对于所有评测用例，1 ≤ N ≤ 100000，−100000 ≤ A i ≤ 100000。

解析:完全二叉树用顺序表存储计算起来那就比较方便了，第一层就2 ^ 0 = 1个结点，第二层 2 ^ 1 = 2个结点,第n层2 ^ (n - 1)个结点。

#include<bits/stdc++.h>
using namespace std;
long long fastPow(long long x,long long n){
	long long sum = 1;
    while(n){
    	if(n & 1) {    //位与运算结果为1,表明幂为奇数 
    		sum *= x;
		}
		    x *= x;//位与运算结果为0,表明幂为偶数
		   n /= 2; //除2 
		}
		return sum;
	}
	
int main(){
	int n;
	cin >> n;
    long long weightMaxSum = LLONG_MIN;//库函数中#include中表示long long数据类型的最小值 
   
    long long depth = 1;//表示完全二叉树的深度
    long long maxWeightSum_Depth = 1;
	for(int i = 1; i <= n; i = fastPow(2,i),depth++){
		 long long weightSum = 0;//表示每一层的权值之和 
		for(int j = 1; j <= fastPow(2,depth - 1);j++){
		int x;
		cin >> x;
		weightSum += x;
		
	    }
	    if(weightSum > weightMaxSum){
		weightMaxSum = weightSum;
		maxWeightSum_Depth = depth;
	    }
		
	} 
	 
	cout <<maxWeightSum_Depth <<endl;
}

试题 H: 等差数列

时间限制: 1.0s 内存限制: 256.0MB 本题总分：20 分

【问题描述】
数学老师给小明出了一道等差数列求和的题目。但是粗心的小明忘记了一
部分的数列，只记得其中 N 个整数。
现在给出这 N 个整数，小明想知道包含这 N 个整数的最短的等差数列有
几项？

【输入格式】
输入的第一行包含一个整数 N。
第二行包含 N 个整数 A 1 ,A 2 ,··· ,A N 。(注意 A 1 ∼ A N 并不一定是按等差数
列中的顺序给出)

【输出格式】
输出一个整数表示答案。

【样例输入】
5
2 6 4 10 20

【样例输出】
10

【样例说明】
包含 2、6、4、10、20 的最短的等差数列是 2、4、6、8、10、12、14、16、18、20。

【评测用例规模与约定】
对于所有评测用例，2 ≤ N ≤ 100000，0 ≤ A i ≤ 10^9 。

解析:这题也算是比较简单的题目了，思路的话就是用一个数组把n个数据存储起来，先把数组排个序，然后设公差为d，对数组中任意连续的两个数求公差di(i=1,2…n-1),则d=gcd(d1,d2…di)，最后利用等差数列性质an - a1 = (n -1) × d求解n即可。

#include<bits/stdc++.h>
using namespace std;
const int N = 100005;
long long gcd(long long n,long long m){
	return m == 0 ? n : gcd(m,n%m);
}	
int main(){
	int n;
	cin >> n;
	long long a[N] = {0};
	for(int i = 0; i < n;i++){
		cin >> a[i];
	}
	sort(a,a + n);
	long long d[N] = {0};
	for(int i = 1;i < n;i++){
		 d[i - 1] = a[i] - a[i - 1];
	}
	int min_d = 0;
	for(int i = 1;i < n - 1;i++){
		min_d = gcd(d[i-1],d[i]); 
	}
	cout << (a[n - 1] - a[0])/min_d + 1; 
     
}

注意，考虑到数据的范围，注意变换使用数据的类型。

试题 I: 后缀表达式

时间限制: 1.0s 内存限制: 256.0MB 本题总分：25 分

【问题描述】
给定 N 个加号、M 个减号以及 N + M + 1 个整数 A 1 ,A 2 ,··· ,A N+M+1 ，小明想知道在所有由这 N 个加号、M 个减号以及 N + M +1 个整数凑出的合法的后缀表达式中，结果最大的是哪一个？
请你输出这个最大的结果。
例如使用1 2 3 + -，则 “2 3 + 1 -” 这个后缀表达式结果是 4，是最大的。

【输入格式】
第一行包含两个整数 N 和 M。
第二行包含 N + M + 1 个整数 A 1 ,A 2 ,··· ,A N+M+1 。

【输出格式】
输出一个整数，代表答案。

【样例输入】
1 1
1 2 3

【样例输出】
4

【评测用例规模与约定】
对于所有评测用例，0 ≤ N, M ≤ 100000，−10 ^ 9 ≤ A i ≤ 10 ^ 9

解析:这题也可以说是非常简单的了，千万别被题目给吓着了，其实思路很简单，就是可以采用逆向思维。我们可以先把输入的数据排个序，并全部加起来，并考虑以下两种情况：
①假设所有输入的数据均为正数。
a)则如果全部符号都为加号，则我们刚才求得的数值即为所求结果。
b)如果符号中含有M个负号，则我们需要将刚才求得的数值减去排序后数据的前M个数的两倍(减两倍的原因是刚才我们加的时候已经算了一次了)

②假设输入的数据中含有负数
a)则如果全部符号都为加号，则我们刚才求得的数值即为所求结果。
b)如果符号中含有M个负号，则我们需要将刚才求得的数值减去排序后数据的前M个数的两倍(这里负负得正就相当于加了)

#include<bits/stdc++.h>
using namespace std;
const int k = 200005;
int main(){
	int N;
	int M;
	cin >> N >> M;
	long long a[k] = {0};
	long long sum = 0;
	for(int i = 0;i < N + M + 1; i++){
	 cin >> a[i];	
	 sum += a[i];
	} 
	sort(a,a + N + M +1);
	if(a[0] >= 0){ // 如果排序后数组第一个数大于0,说明数据中没有负数 
	 if(M){
	 for(int i = 0;i < M;i++){
	 	sum -= 2*a[i];
	 }
      }
  }
	 
	 else{
	 	for(int i = 0; i < k && a[i] < 0 && M > 0;i++,M--){
	 		sum -= 2*a[i];
		 }
	 }
	 cout << sum << endl;  
}

还有两道题一道填空题一道编程题我就不赘述了，还剩下的这道填空题需要用到bfs(广度优先遍历)计算最小步数的思想，还是有一定难度的，还有一道编程题关题目相信就能够看得你脑壳疼，而且还需要用到贪心算法的思想。就我个人观点而言这两道题目应该不能算在水题或者说简单题范畴内，有编程能力比较硬核的大佬不妨可以去专研一下~

因此，本人对于上一届比赛题目的解析到这里就告一段落了，最后希望看到本篇文章的小伙伴本人能够给予到你一定的帮助，希望你在下次比赛中取得好成绩。