平行四边形不等式优化DP

目录

一.前言

二.平行四边形不等式是个啥？

1.题目引入：猴子派对

输入

输出

样例输入

样例输出

2.找出状态转移方程式

3.探索此状态转移方程式的性质

4.细节处理

1.环

2.循环顺序问题

5.更清晰的思维

6.代码

7.变式

1.题目：树的建造

输入

输出

样例输入

样例输出

2.思路

3.样例代码 

三.总结

---

一.前言

DP一直是编程中的一个难题，解决它不仅需要大量刷题，还需要学会各种DP的方法。这里，我就主要讲一个DP的优化方法：平行四边形不等式优化DP动态规划。（好难呀）

 

---

 

二.平行四边形不等式是个啥？

1.题目引入：猴子派对

远离我们的世界，有一个香蕉森林。许多可爱的猴子住在那里。有一天，作为香蕉林之王的SDH（宋大侯）决定举办一个盛大的聚会庆祝疯狂香蕉日。但小猴子彼此不认识，所以作为国王，SDH必须做点什么。 
现在有n只猴子坐成一圈，每只猴子都有交朋友的时间。而且，每只猴子都有两个邻居。SDH希望将它们介绍给对方，规则是：1。每次 ，他只能介绍一只猴子和一只猴子的邻居。 
2.如果他介绍A和B，那么每只已经知道的每只猴子A都知道每只猴子B已经知道了，这次引入的总时间是所有猴子A和B已经知道的交友时间的总和; 
3.每个小猴子都认识自己; 
为了开始聚会并尽快吃香蕉，SDH想知道他需要的最短时间。 

输入

有几个测试用例。在每种情况下，第一行是n（1≤n≤1000），这是猴子的数量。下一行包含n个正整数（小于1000），表示交朋友时间（按顺序，第一个和最后一个是邻居）。输入是文件结尾。

输出

对于每种情况，您应该打印一行，给出SDH引入时的最小时间。

样例输入

8

5 2 4 7 6 1 3 9

样例输出

105

---

2.找出状态转移方程式

大家先不管围成一个圈，先把它们看作一条直线。这道题的状态转移方程式很容易想到：就是在i~j号猴子的范围内，任取一个猴子k，当成是把这个猴子左边的那一堆猴子（i~k）介绍给它右边的那一堆猴子（k+1~j），先预处理计算出i~j号猴子交朋友的总时间w[i][j]，于是，状态转移方程式就出来了：。

---

3.探索此状态转移方程式的性质

这可能有点难得想，大家一定要注意！

以现在的状态转移方程式来看是个三重循环，肯定要超时，不妨让我们来优化一下这个k。k的值肯定无法在每次直接确定，那么我们就缩小它的范围。

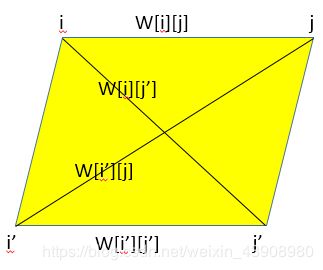
首先，我们来探索一下w[i][j]的性质：有,那么是毋庸置疑的。还有一个性质：，为什么呢？这两个加起来不应该是一样的吗？现在我们用平行四边形来理解一下：

是不是就是这个道理？所以这就是著名的平行四边形不等式。

好，现在找出了w[i][j]的规律，那么如何是k的规律呢？这里有一个专有名词：最佳决策点（k），现在因为用k表示最佳决策点的话不好搞，所以我们用s[i][j]表示dp[i][j]的最佳决策点。因为w[i][j]满足平行四边形不等式，所以s[i][j]也会满足平行四边形不等式（证明过程大家自己想），则有：。我来解释一下为什么:①，意味着在右边少一个猴子。因为我们希望分成的左右两堆猴子基本均匀，这样交友总时间加起来会越少（大家一定想的出来为什么），所以s[i][j-1]的关键决策点绝不会在s[i][j]的右边；②，同理，左边少了一个猴子，关键决策点s[i+1][j]绝不会在s[i][j]的左边。

如此，我们就找出了dp[i][j]的关键决策点的范围了，时间就大大缩小了。

---

4.细节处理

只会个思路什么都不是，现在来想一想代码细节问题：

1.环

这个问题很好处理，共有两种方法：

①截取法

因为我们的思路常常是破环成链，所以我们可以在整个环中每一个位置都破一遍，这有点麻烦。

②补全法

如果我们直接把整个环看成链是会少考虑情况的，不妨在整个链的后面接一个长度为(n-1)的链，这样就能把所有环的情况考虑进去了。

个人推荐用补全法。

2.循环顺序问题

因为我们关键决策点的范围是，所以我们要保证s[i][j-1]和s[i+1][j]都已经求出来了，所以i从大到小循环，j从小到大循环。

求w[i][j]的方法就不用说了吧，直接用前缀和相减就行了。

---

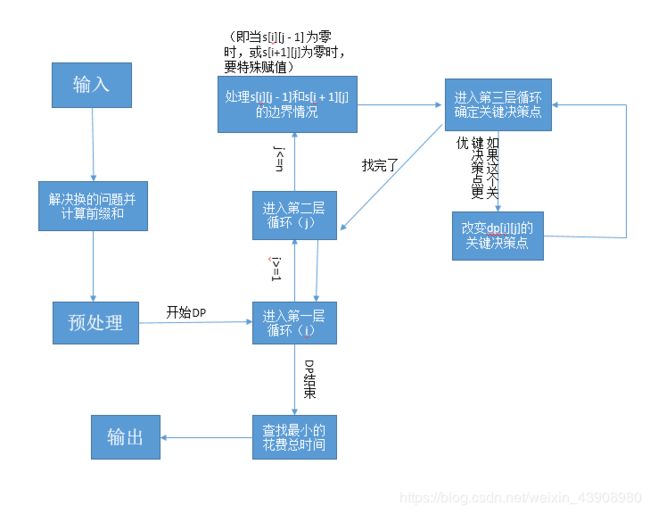
5.更清晰的思维

有点懵，不要慌，大家来看一下这道题的思维图，也许就思路清晰了许多，对平行四边形不等式优化DP有更深刻的意识。

---

6.代码

#include 
#include 
#include 
using namespace std;
#define M 2005
#define INF 0x3f3f3f3f
#define min(a, b) a < b ? a : b
int n, Time[M], dp[M][M], s[M][M], sum[M], ans;
inline void Read (int &x){
	int f = 1; x = 0; char c = getchar();
	while (c > '9' || c < '0') {if (c == '-') f = -1; c = getchar();}
	while (c >= '0' && c <= '9') {x = x * 10 + c - 48; c = getchar();}
	x *= f;
}	
int main (){
    while (~scanf ("%d", &n)){
        ans = INF;
        for (register int i = 1; i <= n; i ++){
            Read (Time[i]);
            sum[i] = sum[i - 1] + Time[i];
        }
        for (register int i = n + 1; i < 2 * n; i ++){//sum[i]是前缀和，我没有求w[i][j]
            Time[i] = Time[i - n];
            sum[i] = sum[i - 1] + Time[i];
        }
        n = n * 2 - 1;
        for (register int i = 0; i <= n; i ++)//预处理
			for (register int j = 0; j <= n; j ++)
				dp[i][j] = INF, s[i][j] = 0;
        dp[0][0] = 0;
        for (register int i = n; i >= 1; i --){
            dp[i][i] = 0;
            for (register int j = i + 1; j <= n; j ++){
                if (!s[i][j - 1])//特殊情况，特殊处理，处理成极限值
                    s[i][j - 1] = min (i + 1, j - 1);
                if (!s[i + 1][j])
                    s[i + 1][j] = j - 1;
                for (register int k = s[i][j - 1]; k <= s[i + 1][j]; k ++){
                    if (dp[i][j] > dp[i][k] + dp[k + 1][j] + sum[j] - sum[i - 1]){//sum[j] - sum[i - 1]即w[i][j]
                        dp[i][j] = dp[i][k] + dp[k + 1][j] + sum[j] - sum[i - 1];
                        s[i][j] = k;
                    }
                }
            }
        }
		n = (n + 1) / 2;
        for (register int i = 1; i <= n; i ++)//找答案
            ans = min (ans, dp[i][i + n - 1]);
        printf ("%d\n", ans);
    }
    return 0;
}

通过这道题，相信大家对平行四边形不等式优化DP有了新的认识，下面来看一道变式。

---

7.变式

1.题目：树的建造

对于所有iYj的点集合（Xi,Yi）的二维空间。我们希望它们都通过一个有向树连接，树的边缘向右（X正）或向上（Y正）。下图显示了一个示例树。

编写一个程序，该程序将所有给定的点与最短的边的总长度连接起来。

输入

输入以包含整数N（1<=N<=1000）的行开始，即点数。然后N行跟随。第i行包含两个整数XI和y(0<=Xi,y<=10000)，它们给出了第i点的坐标。

输出

在一行中打印边的总长度。

样例输入

5
1 5
2 4
3 3
4 2
5 1
1
10000 0

样例输出

12
0

---

2.思路

这道题就有点难了，每一个点是一组坐标。但是可以像上一道题一样解决，并且还没有环，就把每个点看成每个猴子就行了。可以想到，连接i，j点的最小花费是，如图：

于是，先把状态转移方程式写出来：。相信大家一定是后半部分看不懂吧。大家也许想问为何不是。因为这样会加重复，dp[i][k]和dp[k+1][j]内已经有了和了，如果你想以上说的这么加，就会把和又重新加一遍。

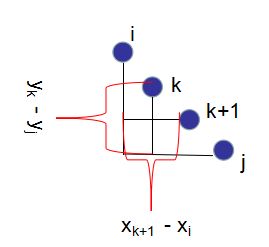
可以借借助一个图来理解：

综上，我们的状态转移方程式就出来了，再利用平行四边形的性质进行优化就行了。

---

3.样例代码 

#include 
#include 
#include 
using namespace std;
#define M 1005
#define INF 0x3f3f3f3f
struct node {
    int x, y;
}a[M];
int n, dp[M][M], s[M][M];
int main (){
    while (~scanf ("%d", &n)){
        for (int i = 1; i <= n; i ++)
            scanf ("%d %d", &a[i].x, &a[i].y);
        memset (dp, INF, sizeof(dp));
        memset (s, 0, sizeof(s));
        dp[0][0] = 0;
        for (int i = n; i >= 1; i --){
            dp[i][i] = 0;
            for (int j = 1 + i; j <= n; j ++){
                if (!s[i][j - 1])
                    s[i][j - 1] = min (i + 1, j - 1);
                if (!s[i + 1][j])
                    s[i + 1][j] = j - 1;
                for (int k = s[i][j - 1]; k <= s[i + 1][j]; k ++){
                    if (dp[i][j] > dp[i][k] + dp[k + 1][j] + a[k].y - a[j].y + a[k + 1].x - a[i].x){
                        dp[i][j] = dp[i][k] + dp[k + 1][j] + a[k].y - a[j].y + a[k + 1].x - a[i].x;
                        s[i][j] = k;
                    }
                }
            }
        }
        printf ("%d\n", dp[1][n]);
    }
    return 0;
}

---

三.总结

相信通过这两道题，大家对平行四边形不等式有了初步的概念，后面还会附上更难的题目，加油！