《自然语言处理(哈工大 关毅 64集视频)》学习笔记:第二章 数学基础与语言学基础
前言
关毅老师,现为哈工大计算机学院语言技术中心教授,博士生导师。通过认真学习了《自然语言处理(哈工大 关毅 64集视频)》1(来自互联网)的课程,受益良多,在此感谢关毅老师的辛勤工作!为进一步深入理解课程内容,对部分内容进行了延伸学习2 3 4,在此分享,期待对大家有所帮助,欢迎加我微信(验证:NLP),一起学习讨论,不足之处,欢迎指正。
![]()
视频列表:
10数学基础与语言学基础 一
11数学基础与语言学基础 二
12数学基础与语言学基础 三
13数学基础与语言学基础 四
14数学基础与语言学基础 五
15数学基础与语言学基础 六
16数学基础与语言学基础 七
10数学基础与语言学基础 一
第二章 数学基础与语言学基础
本章内容
1、数学基础
2、语言学基础
3、实用知识
数学基础介绍
数学与语言学
- 数学
大自然的语言
科学的语言 - 语言学
语言是大自然的产物
语言学是科学的一个分支 - 采用数学的方法描述语言
计算语言学
建立语言的数学模型
有数学基础的方法 vs 没有数学基础的方法
- 有数学基础的方法
美丽的方法
经得起时间考验的方法 - 没有数学基础的方法
打补丁的方法
adhoc(ad hoc)
概率论在语言技术中的应用
- 统计语言处理技术已经成为主流
- 统计语言处理的步骤
- 收集自然语言词汇的分布情况
- 根据这些分布情况进行统计推导
- 最典型的例子:构造统计语言模型
- 概率论是统计语言模型的数学基础
概率论回顾
- 概率论是研究随机现象的数学分支
- 所谓随机现象是指这样的一类现象,当人们观察它时, 所得到的观察结果不是确定的,而是许许多多可能结果中的一种
- 概率(Probability)则是衡量该事件发生的可能性的量度
概率
-
样本空间 Ω 是一个随机试验所有可能的结果的集合
-
事件 A 是Ω的子集
-
概率函数 (或者概率分布)
P : Ω → [ 0 , 1 ] P:\Omega \rightarrow [0,1] P:Ω→[0,1] -
某字或者某词出现的概率是多少?
示例1:
现代汉语字频统计–由北京航空学院和国家语言文字工作委员会于1985年完成。从1977年至1982年间社会科学和自然科学的规模为一千一百零八万余字的语料中利用计算机进行统计得到汉字的字频,前20个最高频汉字列出如表所示:

示例24:
在语言处理中使用频率分布,NLTK 中内置FreqDist,让我们使用FreqDist 寻找《白鲸记》中最常见的50 个词。
from pylab import *
%matplotlib inline
from nltk.book import *
*** Introductory Examples for the NLTK Book ***
Loading text1, …, text9 and sent1, …, sent9
Type the name of the text or sentence to view it.
Type: ‘texts()’ or ‘sents()’ to list the materials.
text1: Moby Dick by Herman Melville 1851
text2: Sense and Sensibility by Jane Austen 1811
text3: The Book of Genesis
text4: Inaugural Address Corpus
text5: Chat Corpus
text6: Monty Python and the Holy Grail
text7: Wall Street Journal
text8: Personals Corpus
text9: The Man Who Was Thursday by G . K . Chesterton 1908
《白鲸记》(Moby Dick by Herman Melville 1851)
fdist1 = FreqDist(text1)
print(fdist1)
第一次调用FreqDist 时,传递文本的名称作为参数。我们可以看到已经被计算出来的《白鲸记》中的总的词数(“结果”)——高达260,819。
print(fdist1.most_common(50))
[(’,’, 18713), (‘the’, 13721), (’.’, 6862), (‘of’, 6536), (‘and’, 6024), (‘a’, 4569), (‘to’, 4542), (’;’, 4072), (‘in’, 3916), (‘that’, 2982), ("’", 2684), (’-’, 2552), (‘his’, 2459), (‘it’, 2209), (‘I’, 2124), (‘s’, 1739), (‘is’, 1695), (‘he’, 1661), (‘with’, 1659), (‘was’, 1632), (‘as’, 1620), (’"’, 1478), (‘all’, 1462), (‘for’, 1414), (‘this’, 1280), (’!’, 1269), (‘at’, 1231), (‘by’, 1137), (‘but’, 1113), (‘not’, 1103), (’–’, 1070), (‘him’, 1058), (‘from’, 1052), (‘be’, 1030), (‘on’, 1005), (‘so’, 918), (‘whale’, 906), (‘one’, 889), (‘you’, 841), (‘had’, 767), (‘have’, 760), (‘there’, 715), (‘But’, 705), (‘or’, 697), (‘were’, 680), (‘now’, 646), (‘which’, 640), (’?’, 637), (‘me’, 627), (‘like’, 624)]
这50 个词在书中的分布情况,如下:
fdist1.plot(50, cumulative=False)
10数学基础与语言学基础 二
汉字的信息熵
信息熵
香农1948年发表了著名的论文《通讯的数学理论》,宣告了信息论的诞生。在这篇论文中,他选择概率论作为数学工具,提出了用“不确定性的量度”来计算信息量的数学公式,为信息论奠定了理论基础。
H ( p ) = ∑ x ∈ Ω − p ( x ) log p ( x ) H(p) ={\sum_{}^{x\in \Omega }} - p(x) \log p(x) H(p)=∑x∈Ω−p(x)logp(x)
示例4:
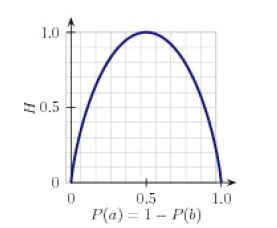
上图显示了在名字性别预测任务中标签的熵如何取决于男性名字对女性名字的比例。请注意,如果大多数输入值具有相同的标签(例如,如果P(male)接近0 或接近1),那么熵很低。特别的,低频率的标签不会贡献多少给熵(因为P(l)很小),高频率的标签对熵也没有多大帮助(因为 log e P ( I ) \log_{e}P(I) logeP(I)很小)。另一方面,如果输入值的标签变化很多,那么有很多“中等”频率的标签,它们的 P ( l ) P(l) P(l)和 log e P ( I ) \log_{e}P(I) logeP(I)都不小,所以熵很高。下面 演示如何计算标签链表的熵。
import math
import nltk
def entropy(labels):
freqdist = nltk.FreqDist(labels)
probs = [freqdist.freq(l) for l in freqdist]
return -sum(p * math.log(p,2) for p in probs)
print(entropy(['male', 'male', 'male', 'male']))
-0.0
print(entropy(['male', 'female', 'male', 'male']))
0.8112781244591328
print(entropy(['female', 'male', 'female', 'male']))
1.0
print(entropy(['female', 'female', 'male', 'female']))
0.8112781244591328
print(entropy(['female', 'female', 'female', 'female']))
-0.0
汉字是世界上信息量最大的文字符号系统
- 每收到一个英文讯号消除的不确定程度H 是4.1606比特。
- 汉字的信息熵随着汉字个数的增加而增加,当汉字的个数达到12366个汉字时,汉字的信息熵值为9.65(冯志伟)

- 汉字是当今世界上信息量最大的文字符号系统
几点认识
条件概率
- 对于随机试验的结果有部分知识(或者约束条件)
- 条件概率(Conditional probability)
- 已知B为真的条件下A 为真的概率可以表示为P(A|B)
- 先验概率(prior probability)
- 后验概率(posterior probability)
示例1:
P ( 大 学 ) = 0.0003 P(大学)=0.0003 P(大学)=0.0003
P ( 大 学 ∣ 工 业 ) = P ( 工 业 大 学 ) / P ( 工 业 ) > P ( 大 学 ) P(大学|工业)=P(工业大学)/P(工业) > P(大学) P(大学∣工业)=P(工业大学)/P(工业)>P(大学)
示例24:
概率分布计算观察到的事件,如文本中出现的词汇。条件概率分布需要给每个时间关联一个条件,所以不是处理一个词序列,我们必须处理的是一个配对序列。
text = [‘The’, ‘Fulton’, ‘County’, ‘Grand’, ‘Jury’, ‘said’, …]
pairs = [(‘news’, ‘The’), (‘news’, ‘Fulton’), (‘news’, ‘County’), …]
每对的形式是:(条件,事件)。如果我们按文体处理整个布朗语料库,将有15 个条件(每个文体一个条件)和1,161,192 个事件(每一个词一个事件)。
按文体计数词汇,FreqDist()以一个简单的链表作为输入,ConditionalFreqDist()以一个配对链表作为输入。
import nltk
from nltk.corpus import brown
cfd = nltk.ConditionalFreqDist(
(genre, word)
for genre in brown.categories()
for word in brown.words(categories=genre))
genre_word = [(genre, word)
for genre in ['news', 'romance']
for word in brown.words(categories=genre)]
len(genre_word)
170576
genre_word[:4]
[(‘news’, ‘The’), (‘news’, ‘Fulton’), (‘news’, ‘County’), (‘news’, ‘Grand’)]
genre_word[-4:]
[(‘romance’, ‘afraid’), (‘romance’, ‘not’), (‘romance’, “’’”),(‘romance’, ‘.’)]
现在,我们可以使用此配对链表创建一个ConditionalFreqDist,并将它保存在一个变量cfd 中。
cfd = nltk.ConditionalFreqDist(genre_word)
print(cfd)
cfd.conditions()
[‘romance’, ‘news’]
print(cfd['news'])
print(cfd['romance'])
print(list(cfd['romance']))
[‘conclusion’, ‘lucky’, ‘treat’, ‘Eph’, ‘darned’, ‘Got’, ‘sloppy’,…]
cfd['romance']['could']
193
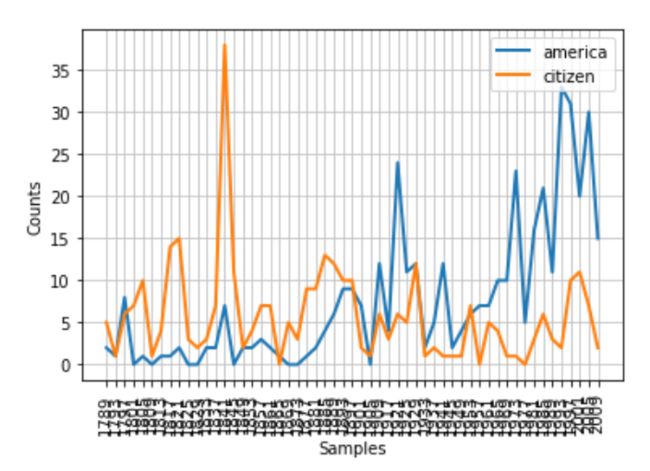
图2.1条件频率分布图:计数就职演说语料库中所有以america 或citizen 开始的词。每个演讲单独计数。这样就能观察出随时间变化用法上的演变趋势。
from pylab import *
%matplotlib inline
from nltk.book import *
import nltk
from nltk.corpus import inaugural
cfd = nltk.ConditionalFreqDist(
(target, fileid[:4])
for fileid in inaugural.fileids()
for w in inaugural.words(fileid)
for target in ['america', 'citizen']
if w.lower().startswith(target))
cfd.plot()
联合概率
- P ( A , B ) = P ( A ) P ( B ∣ A ) = P ( B ) P ( A ∣ B ) P(A,B)=P(A)P(B|A)=P(B)P(A|B) P(A,B)=P(A)P(B∣A)=P(B)P(A∣B)
- a r g m a x f ( x ) x \underset{x}{argmaxf(x)} xargmaxf(x)使 f ( x ) f(x) f(x) 值为最大的那个
a r g m a x A P ( B ∣ A ) P ( A ) P ( B ) ) = a r g m a x A P ( B ∣ A ) P ( A ) \underset{A}{argmax}\frac{P(B|A)P(A)}{P(B)})=\underset{A}{argmax}P(B|A)P(A) AargmaxP(B)P(B∣A)P(A))=AargmaxP(B∣A)P(A) - 联合概率的链规则:
P ( A , B , C , D … ) = P ( A ) P ( B ∣ A ) P ( C ∣ A , B ) P ( D ∣ A , B , C . . ) P(A,B,C,D…) = P(A)P(B|A)P(C|A,B)P(D|A,B,C..) P(A,B,C,D…)=P(A)P(B∣A)P(C∣A,B)P(D∣A,B,C..)
示例:
P ( 哈 尔 滨 / 工 业 / 大 学 ) = P ( 哈 尔 滨 ) P ( 工 业 ∣ 哈 尔 滨 ) P ( 大 学 ∣ 哈 尔 滨 , 工 业 ) P(哈尔滨/工业/大学)=P(哈尔滨)P(工业|哈尔滨)P(大学|哈尔滨,工业) P(哈尔滨/工业/大学)=P(哈尔滨)P(工业∣哈尔滨)P(大学∣哈尔滨,工业)
独立
- 两个事件 A 与 B 相互独立,如果 P ( A ) = P ( A ∣ B ) ↔ P ( A , B ) = P ( A ) ∗ P ( B ) P(A) =P(A|B)↔P(A,B)=P(A)*P(B) P(A)=P(A∣B)↔P(A,B)=P(A)∗P(B)
条件独立
两个事件 A 与 B 是在条件C下相互条件独立如果: P ( A ∣ C ) = P ( A ∣ B , C ) P(A|C) = P(A|B,C) P(A∣C)=P(A∣B,C)
10数学基础与语言学基础 三
贝叶斯定理(Bayes’ Theorem)
- 贝叶斯定理的最简形式
P ( A ∣ B ) = P ( A , B ) P ( B ) = P ( B ∣ A ) P ( A ) P ( B ) P(A|B)=\frac{P(A,B)}{P(B)}=\frac{P(B|A)P(A)}{P(B)} P(A∣B)=P(B)P(A,B)=P(B)P(B∣A)P(A)
- Bayes’Theorem使我们能够交换事件之间的条件依赖顺序
a r g m a x A P ( A ∣ B ) = a r g m a x A P ( B ∣ A ) P ( A ) P ( B ) ) = a r g m a x A P ( B ∣ A ) P ( A ) \underset{A}{argmax}P(A|B)=\underset{A}{argmax}\frac{P(B|A)P(A)}{P(B)})=\underset{A}{argmax}P(B|A)P(A) AargmaxP(A∣B)=AargmaxP(B)P(B∣A)P(A))=AargmaxP(B∣A)P(A)
贝叶斯定理的应用实例
- 音字转换
a r g m a x T P ( T ∣ S ) = a r g m a x T P ( S ∣ T ) P ( T ) P ( S ) ) = a r g m a x T P ( S ∣ T ) P ( T ) \underset{T}{argmax}P(T|S)=\underset{T}{argmax}\frac{P(S|T)P(T)}{P(S)})=\underset{T}{argmax}P(S|T)P(T) TargmaxP(T∣S)=TargmaxP(S)P(S∣T)P(T))=TargmaxP(S∣T)P(T)
这里, P ( S ∣ T ) P(S|T) P(S∣T)字音转换模型, P ( T ) P(T) P(T)语言模型,显然构造 P ( S ∣ T ) P(S|T) P(S∣T) 与 P ( T ) P(T) P(T)的难度较直接构造 P ( T ∣ S ) P(T|S) P(T∣S)大大地降低了
随机变量
随机变量(Random variables)(RV)使我们能够讨论与样本空间相关的数值的概率值
- 离散型随机变量
在某一时间点出现的单词可以视为(离散型)随机变量,语言可视为以时间为序的一组随机变量的序列
T = w 1 w 2 w 3 . . . w t . . . w n T=w_{1}w_{2}w_{3}...w_{t}...w_{n} T=w1w2w3...wt...wn - 连续型随机变量
数学期望与方差
- 数学期望:随机变量的均值
E ( x ) = μ = ∑ x x p ( x ) E(x)=\mu ={\sum_{}^{x}}{xp(x)} E(x)=μ=∑xxp(x) - 方差:随机变量取值是否比较一致或者有很大差异的一个量度
V a r ( x ) = E ( ( X − E ( X ) ) 2 ) = E ( X 2 ) − E ( X ) 2 = σ 2 Var(x)=E((X-E(X))^{2})=E(X^{2})-E(X)^{2}=\sigma ^{2} Var(x)=E((X−E(X))2)=E(X2)−E(X)2=σ2
σ \sigma σ称为标准差 - 应用示例-新词发现
统计大规模语料中字A与字B的间隔字数的数学期望与方差,假设方差很小,比如小于某个阈值,那么A…B很可能成词
构造语言模型P(T)的两类方法
- 基于频度的统计
- 贝叶斯统计
基于频度的统计
相关频度(频率):事件 μ \mu μ发生的次数与所有事件总次数的比率
f ( μ ) = C ( μ ) N f(\mu) = \frac{C(\mu)}{N} f(μ)=NC(μ)
在 N N N次实验中 μ \mu μ发生的次数,当 N → ∞ , f ( μ ) N\rightarrow \infty ,f(\mu) N→∞,f(μ)逐渐稳定在某个数值上,作为该事件的概率估计
- 有参数的方法(Parametric)(与分布有关)
假设某种语言现象服从我们业已熟知的某种分布, 如二元分布,正态分布,泊松分布等等,我们已有明确的概率模型,现在需要确定该概率分布的一些参数。
常用分布
- 二元分布(Binomial distribution)
在英语语料库中,包含单词“the”的语句占语料库中语句总数的比例近似地服从二项分布 - 泊松分布(Poisson distribution)
在某一固定大小的范围(或者时间段)内,某种特定类型事件的分布 - 正态分布 (高斯分布Gaussian distribution)(Normal distribution)
汉字的笔画数与该笔画对应的汉字的个数符合正态分布
- 无参数的方法(Non-parametric)(与分布无关)
对数据的分布没有预先的分布假设
仅仅通过最大相似度估计来估算P
先验知识比较少,但需要大规模的训练数据
本课主要探讨无参数的方法
贝叶斯统计
- 贝叶斯统计的实质是可信度数量化
- 可信度是这样计算出来的
- 有先验的知识
- 根据数据应用贝叶斯定理更新知识
M ∗ = a r g m a x M P ( M ∣ D ) = a r g m a x M P ( D ∣ M ) P ( M ) P ( D ) ) = a r g m a x M P ( D ∣ M ) P ( M ) M^{*} = \underset{M}{argmax}P(M|D) = \underset{M}{argmax}\frac{P(D|M)P(M)}{P(D)})= \underset{M}{argmax}P(D|M)P(M) M∗=MargmaxP(M∣D)=MargmaxP(D)P(D∣M)P(M))=MargmaxP(D∣M)P(M) - 先验的概率分布 P ( M ) P(M) P(M),
- 当新的数据到来后,根据贝叶斯公式计算 P ( M ∣ D ) P(M|D) P(M∣D).
- P ( M ∣ D ) P(M|D) P(M∣D)成为新的概率模型
- 如此反复
其他数学基础
- 信息论
- 集合论
- 函数与关系
- 微积分
- 粗糙集
……
10数学基础与语言学基础 四
语言学基础
汉语语言学基础
自然语言处理系统中的语言知识库
- 自然语言处理系统可以直接利用的机器词典中的语言知识包含了词法、句法、语义和语用等各个层面的信息。
- 词法和句法信息总是最基本的,也是研究得比较成熟的
- 现代汉语语义资源已经出现(hownet, 中文wordnet)
现代汉语词语的语法功能分类
基本词类
实词
体词
- 名词(n):例如,牛、书、水、教授、国家、心胸、北京
- 时间词(t):例如,明天、元旦、唐朝、现在、春天
- 处所词(s):例如,空中、低处、郊外
- 方位词(f):例如,上、下、前、后、东、西、南、北
- 数词(m):例如,一、第一、千、零、许多、百万
- 量词(q):例如,个、群、克、杯、片、种、些
- 代词® (体词性):例如,你、我们、这、哪儿、谁
谓词
- 代词® (谓词性):例如,这样
- 动词(v):例如,走、休息、同意、能够、出去、是、调查
- 形容词(a):例如,好、红、大、温柔、美丽、突然
- 状态词(z):例如,雪白、金黄、泪汪汪、满满当当、灰不溜秋
其他实词
- 区别词(b):例如,男、女、公共、微型、初级
- 副词(d):例如,不、很、都、刚刚、难道、忽然
虚词
- 介词§:例如,把、被、对于、关于、以、按照
- 连词©:例如,和、与、或、虽然、但是、不但、而且
- 助词(u):例如,了、着、过、的、得、所、似的
- 语气词(y):例如,吗、呢、吧、嘛、啦
- 拟声词(o):例如,呜、啪、丁零当啷、哗啦
- 叹词(e):例如,哎、喔、哦、啊
附加类别与标点符号
小于词的单位
- 前接成分(h): 阿,老,超
- 后接成分(k): 儿, 子, 性, 员, 器
- 语素字 (g): 柿, 衣, 失, 遥, 郝
- 非语素字(x): 鹌, 枇, 蚣
大于词的单位
- 成语 (i) : 胸有成竹, 八拜之交
- 习用语 (l) : 总而言之, 由此可见
- 简称略语(j) : 三好, 全总
标点符号
各类词语的主要特点
实词的主要特点
- 开放类
- 能单独充当某种句法成分
- 位置不固定
- 具有较强的构词力
- 有比较具体的词义
虚词的主要特点
- 封闭类
- 不能充当句法成分
- 粘着性
- 位置比较固定
- 没有具体的词义
体词和谓词
- 体词和谓词都属于实词
- 体词主要语法功能是作主语、宾语,一般不作谓语。
- 谓词的主要功能是作谓语,也能作主语和宾语
名词
- 名词是典型的体词
- 一般不受副词修饰
- 可以受数量词修饰
- 名词可以修饰名词
- 名词不能带表示时态的助词
- 名词不能做状语
动词
- 是最典型最重要的谓词
- 能带真宾语的谓词都是动词(及物动词)
- 不能带真宾语的谓词包括不及物动词、形容词和状态词
- 动名兼类
- 能愿动词(助动词)
- 动词的形态变化比较丰富(VV,V一V,ABAB等等)
形容词
- 是一类重要的谓词
- 能直接受“很”一类程度副词修饰且不能带真宾语的谓词是形容词。形容词可以带准宾语。
- 绝大多数形容词可以受否定副词“不”修饰
- 可以带补语
- 名形兼类
- 形动兼类
- 形容词的形态变化(AA,ABAB)
10数学基础与语言学基础 五
汉语的句法分析的特点
汉语句法分析的特殊性
- 汉语是一种“孤立语”
“孤立语”、“屈折语”、“粘着语” - 同一词类可担任多种句法成分且无形态变化
- 汉语句子的构造规则与短语的构造规则基本一致
- 汉语的语序
在短语内部语序严格固定
短语间语序比较灵活 - 虚词经常可以省略,增加了语法分析的困难
- 汉语词切分有歧义
语言知识库
- 语言知识库是自然语言处理系统不可或缺的组成部分
- 语言知识库的规模和质量在很大程度上决定了自然语言处理系统的成败
北大计算语言研究所的相关工作
- 现代汉语语法信息词典
- 大规模现代汉语基本标注语料库
- 面向汉英机器翻译的现代汉语语义词典
- 英汉、日汉对照双语语料库
- 多个专业领域的术语库
- 现代汉语短语结构规则库
- 中国古代诗词语料库
- …
示例
- 音字转换系统语言知识库
…
机器 ji1qi4
激起 ji1qi3
吉期 ji2qi3
极其 ji2qi2
及其 ji2qi2
… - 现代汉语语义词典
…
安乐/形 D378
安理会/名 L16
安谧/形 D405
安眠/动 C133
安眠药/名 C235
…
什么是 Ontology
- 定义
An ontology consists of a set of concepts, axioms, and relationships that describe a domain of interest
Standard Upper Ontology (SUO) Working Group - 中文译为“本体”
- 可以理解为知识库
- 不同领域有不同的ontology
- 我们关心的是语言ontology,又称语言本体
- 语言本体通常特指语义知识库,而语言知识库则泛指词汇、语法、语义知识库
面向计算机的词汇语义资源必须具备如下特点
- 高度形式化、可计算
- 揭示多重语义关系网络
- 接受信息处理系统检验和评测
Hownet
董振东,董强 www.keenage.com
是一个以汉语和英语的词语所代表的概念为描述对象,以揭示概念与概念之间以及概念所具有的属性之间的关系为基本内容的常识知识库 -董振东
- 知网概况
汉字 7108
词汇 83397
英语单词和短语 79246
中文语义定义 97764
英文语义定义 98963
10数学基础与语言学基础 六
词类统计:
ADJ: 11648
ADV: 1513
NOUN: 46412
VERB: 25742
…
词长度统计
词长=1: 6905
词长=2: 45724
词长=3: 13681
词长=4: 13822
词长=5: 1649
…
词汇的同义、反义、对义集合
上下位概念
“火车”
上位概念:entity|实体
==> thing|万物
==> physical|物质
==> inanimate|无生物
==> artifact|人工物
==> implement|器具
==> vehicle|交通工具
==> LandVehicle|车



10数学基础与语言学基础 七
基于知网的词汇语义相似度计算
- 语义相似度
- 基于语言知识库的语义相似度计算
- 基于统计的语义相似度计算
如何构造比较专业的语言知识库
机器可读词典
- Machine readable dictionary
- lexicon
构造 lexicon的方法
- 文本文件方式
- 数据库
- 二进制文件方式
二进制文件方式
typedef struct HeadWordItem {
int Wordid;
unsigned char ChineseString[MAXWORDLEN];
int freq;
} HeadWordItem;
typedef struct Lexicon {
char LicenseInfo[256];
int Item_Number_of_Lexicon_Head;
int Item_Number_of_Lexicon_Body;
HeadWordItem LexiconHead[HEAD_LEN];
} Lexicon;
- 构建
Lexicon * lexicon=new Lexicon;
…
fopen(…“w+b”)
fwrite(lexicon,sizeof(Lexicon),1,lexiconfile)
fclose(…) - 读取
fread - 更新
- 内存指针操作
lexicon->LexiconHead[i].freq++; - 访问
Binary search
Hash - 写入
fwrite(…)
fclose(…)
参考文献
《自然语言处理(哈工大 关毅 64集视频)》(来自互联网) ↩︎
王晓龙、关毅 《计算机自然语言处理》 清华大学出版社 2005年 ↩︎
哈工大语言技术平台云官网:http://ltp.ai/ ↩︎
Steven Bird,Natural Language Processing with Python,2015 ↩︎ ↩︎ ↩︎ ↩︎