矩阵连乘问题——算法笔记——详解
1、动态规划法
问题简述:
给定n个矩阵{A1A2…An},其中Ai和Ai+1是可乘的,考察这n个矩阵的连乘积A1A2…An。由于矩阵的乘法满足结合律,故计算矩阵的连乘积有许多不同的计算次序,而不同的计算次序,所需要计算的连乘次数也是不同的,求解连乘次数最少的矩阵连乘最优次序。
举例说明矩阵结合方式对数乘次数的影响:
矩阵连乘积A1A2A3,3个矩阵的维数分别为10x100,100x5和5x50,连乘时加括号的方式有:
((A1*A2)*A3) 数乘次数:10*100*5+10*5*50=7500
(A1*(A2*A3)) 数乘次数:100*5*50+10*100*50=75000
- 以矩阵链ABCD为例
- 按照矩阵链长度递增计算最优值
- 矩阵链长度为1时,分别计算出矩阵链A、B、C、D的最优值
- 矩阵链长度为2时,分别计算出矩阵链AB、BC、CD的最优值
- 矩阵链长度为3时,分别计算出矩阵链ABC、BCD的最优值
- 矩阵链长度为4时,计算出矩阵链ABCD的最优值
解答:我们按照动态规划的几个步骤来分析:
(1)找出最优解的性质,刻画其特征结构
对于矩阵连乘问题,最优解就是找到一种计算顺序,使得计算次数最少。
令m[i][j]表示第i个矩阵至第j个矩阵这段的最优解。
将矩阵连乘积 简记为A[i:j] ,这里i<=j.假设这个最优解在第k处断开,i<=k (2)建立递归关系 (相当于对i~j这段,把它分成2段,看哪种分法乘的次数最少,如A1,A2,A3,A4,则有3种分法:{A1}{A2A3A4 }、{A1A2}{A3A4 }、{A1A2A3}{A4 },其中{}表示其内部是最优解,如{A1A2A3}表示是A1A2A3的最优解), 对于1≤i≤j≤n不同的有序对(i,j) 对于不同的子问题,因此不同子问题的个数最多只有o(n*n).但是若采用递归求解的话,许多子问题将被重复求解,所以子问题被重复求解,这也是适合用动态规划法解题的主要特征之一。 用动态规划算法解此问题,可依据其递归式以自底向上的方式进行计算。在计算过程中,保存已解决的子问题答案。每个子问题只计算一次,而在后面需要时只要简单查一下,从而避免大量的重复计算,最终得到多项式时间的算法。 对于 p={30 35 155 10 20 25}: (A1A2A3),(A2A3A4),(A3A4A5),(A4A5A6)这4个矩阵段(长度为3)的最优解.当i=2时(A2A3A4)的最优解为{A2(A3A4) ,(A2A3)A4}的较小值。 同理比如 下面代码中后面的k也相当于是从i到j-1递增的,只是单独把第一个(k=i)提了出来. 下面给出动态规划求解最优值的代码: ABCD四个矩阵连乘 对于上面四个矩阵来说,枚举方法是: 程序实现 备忘录方法是动态规划算法的变形,与动态规划算法一样,备忘录算法用表格保存已解决的子问题的答案,在下次需要解此问题时只是简单地查看该问题的答案,而不必重新计算。与动态规划算法不同的是,备忘录算法的递归方式是自顶向下的,而动态规划算法是自底向上的。 上图为递归枚举过程,小方块内的1:4代表第1个矩阵至第4个矩阵的完全加括号方式 可以看到黄色方块中有很多重复计算,所以利用备忘录来保存计算结果,在每次进行计算前, 程序实现 参考自:
设计算A[i:j],1≤i≤j≤n,所需要的最少数乘次数m[i,j],则原问题的最优值为m[1,n] 。当i=j时,A[i,j]=Ai, m[i,j]=0;(表示只有一个矩阵,如A1,没有和其他矩阵相乘,故乘的次数为0)
当i

计算顺序为:
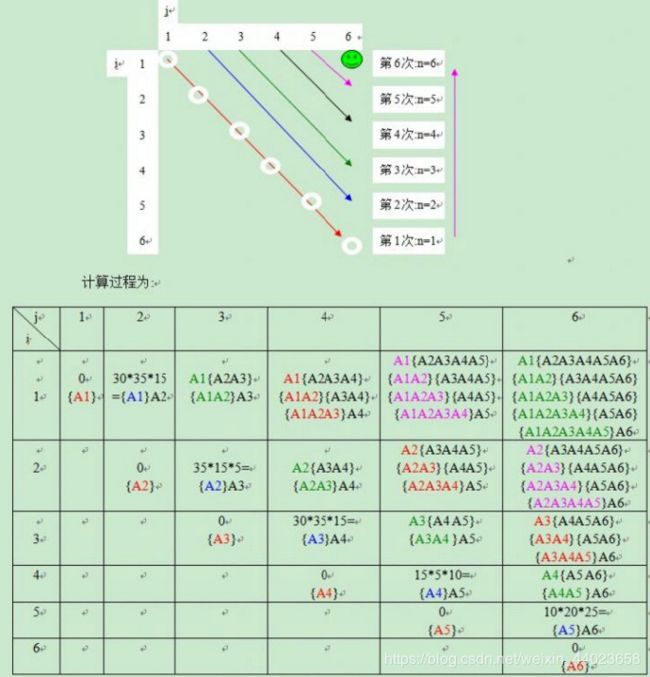 对上例,共6个矩阵(A1~A6),n=6,当r=3时,r循环里面的是3个矩阵的最优解,i从1->4,即求的是
对上例,共6个矩阵(A1~A6),n=6,当r=3时,r循环里面的是3个矩阵的最优解,i从1->4,即求的是当R=2时,迭代计算出:
m[1:2]=m[1:1]+m[2:2}+p[0]*p[1]*p[2];
m[2:3]=m[2:2]+m[3:3]+p[1]*p[2]*p[3];
m[3:4]=m[3:3]+m[4][4]+p[2]*p[3]*p[4];
m[4:5]=m[4:4]+m[5][5]+p[3]*p[4]*p[5];
m[5:6]=m[5][5]+m[6][6]+p[4]*p[5]*p[6];
当R=3时,迭代计算出:
m[1:3]=min(m[1:1]+m[2:3]+p[0]*p[1]*p[3],m[1:2]+m[3:3]+p[0]*p[2]*p[3]);
m[2:4]=min(m[2:2]+m[3:4]+p[1]*p[2]*p[4],m[2:3]+m[4:4]+p[1]*p[3]*p[4]);
......
m[4:6]=min(m[4:4]+m[5:6]+p[3]*p[4]*p[6],m[4:5]+m[6:6]+p[3]*p[5]*p[6]);
......
void MatrixChain(int *p,int n,int **m,int **s)
{ //m是最优值,s是最优值的断开点的索引,n为题目所给的矩阵的个数(下面例子中)
//矩阵段长度为1,则m[][]中对角线的值为0,表示只有一个矩阵,没有相乘的.
for(int i = 1;i<=n;i++) m[i][i] = 0; //本题中n=6
for(int r = 2;r<=n;r++){//对角线循环,r表示矩阵的长度(2,3…逐渐变长)
for(int i = 1;i<=n-r+1;i++){ //行循环
//从第i个矩阵Ai开始,长度为r,则矩阵段为(Ai~Aj)
int j = r+i-1;//列的控制,当前矩阵段(Ai~Aj)的起始为Ai,尾为Aj
//求(Ai~Aj)中最小的,其实k应该从i开始,但先记录第一个值,k从i+1开始,这样也可以。
//例如对(A2~A4),则i=2,j=4,下面一行的m[2][4]=m[3][4]+p[1]*p[2]*p[4],即A2(A3A4)
m[i][j] = m[i+1][j] + p[i-1]*p[i]*p[j];
s[i][j] = i;//记录断开点的索引
//循环求出(Ai~Aj)中的最小数乘次数
for(int k = i+1 ; k<j;k++){
//将矩阵段(Ai~Aj)分成左右2部分(左m[i][k],右m[k+1][j]),
//再加上左右2部分最后相乘的次数(p[i-1] *p[k]*p[j])
int t = m[i][k] + m[k+1][j] + p[i-1] *p[k]*p[j];
if(t<m[i][j])
{ m[i][j] = t;
s[i][j] = k; //保存最小的,即最优的结果
}//if
}//k
}//i
}//r
}//MatrixChain
2、枚举法
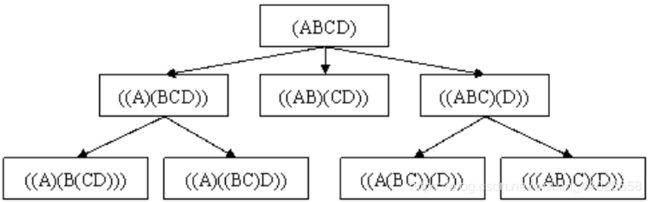
1、(A(BCD))——>(A(B(CD))),(A((BC)D));
2、((AB)(CD))——>NULL;
3、((ABC)D)——>((A(BC)D)),(((AB)C)D);
1、括号加在A和B之间,矩阵链被分为(A)和(BCD);
2、括号加在B和C之间,矩阵链被分为(AB)和(CD);
3、括号加在C和D之间,矩阵链被分为(ABC)和(D);
在第一步中分出的(A)已经不能在加括号了,所以结束;
而(BCD)继续按照上面的步奏把括号依次加在B和C、C和D之间,其他情况相同。
加括号的过程是递归的。//m数组内存放矩阵链的行列信息
//m[i-1]和m[i]分别为第i个矩阵的行和列(i = 1、2、3...)
int Best_Enum(int m[], int left, int right)
{
//只有一个矩阵时,返回计算次数0
if (left == right)
{
return 0;
}
int min = INF; //无穷大
int i;
//括号依次加在第1、2、3...n-1个矩阵后面
for (i = left; i < right; i++)
{
//计算出这种完全加括号方式的计算次数
int count = Best_Enum(m, left, i) + Best_Enum(m, i+1, right);
count += m[left-1] * m[i] * m[right];
//选出最小的
if (count < min)
{
min = count;
}
}
return min;
}
3、备忘录法优化
备忘录方法为每个子问题建立一个记录项,初始化时,该记录项存入一个特殊的值,表示该子问题尚未求解,对每个待求的子问题,首先查看其记录项。若记录项是原始值,则代表该问题是第一次遇到,计算该问题的值并保存;若记录项中存储的不是初始化时的特殊值,则表示子问题已经被计算过,此时只要从记录项中取出该子问题的解答即可,不必重新计算。

先查表,看是否计算过,避免重复计算。#include
陈斌彬的技术博客
庞老板
