百度2017春招笔试真题编程题集合题解
百度2017春招笔试真题编程题集合题解
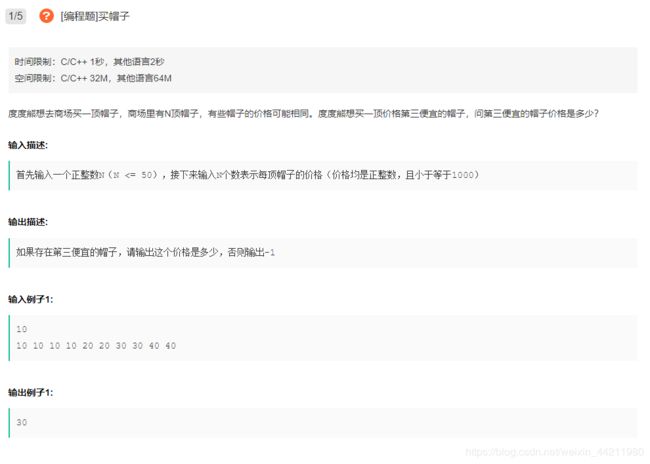
【题1】
【解题思路】
水题,随便写写
【AC代码】
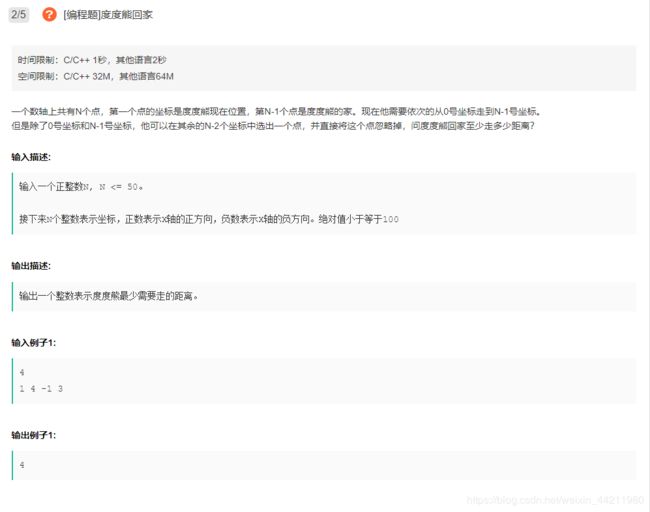
#include 【题2】
【解题思路】
暴力枚举每个点被去除的情况,找到最优解
【AC代码】
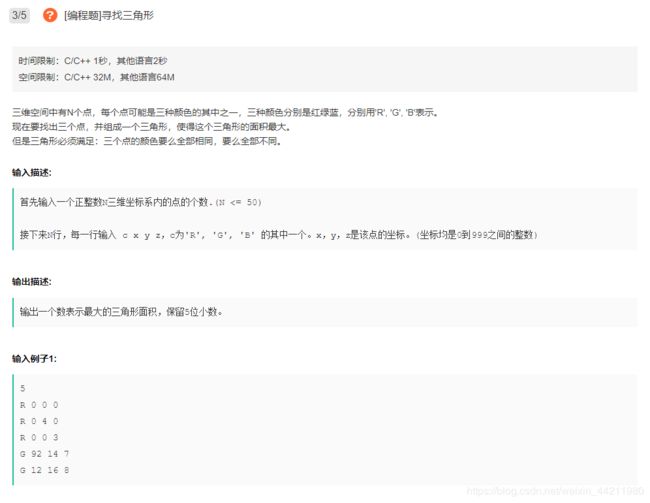
#include 【题3】
【解题思路】
水题,有很多情况数据没卡,比如共线,点重合等情况,暴力枚举+海伦公式
【AC代码】
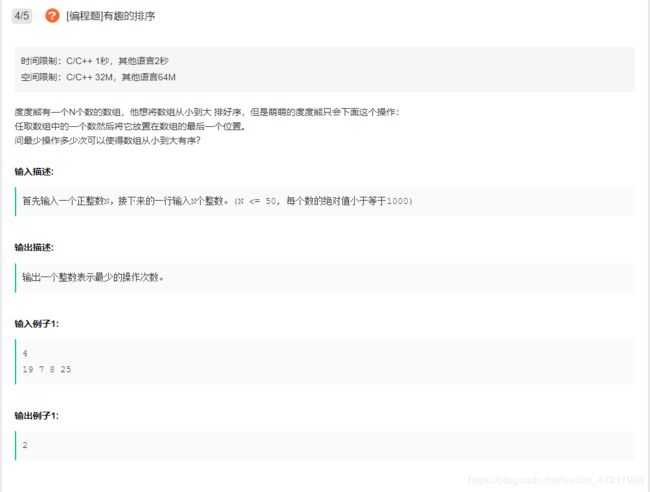
#include 【题4】
【解题思路】
本质类似于最长上升子序列,但又不尽相同
举个例子
原序列:3 4 1 2 6 8 9
排序后:1 2 3 4 6 8 9
原下标:3 4 1 2 5 6 7
可以发现原序列中下标为3和4的元素是没有移动的,而其他元素全部都移动了,所以最小的移动次数应该为7-2=5,即元素总个数n减去排序后从前往后有序的个数m
【AC代码】
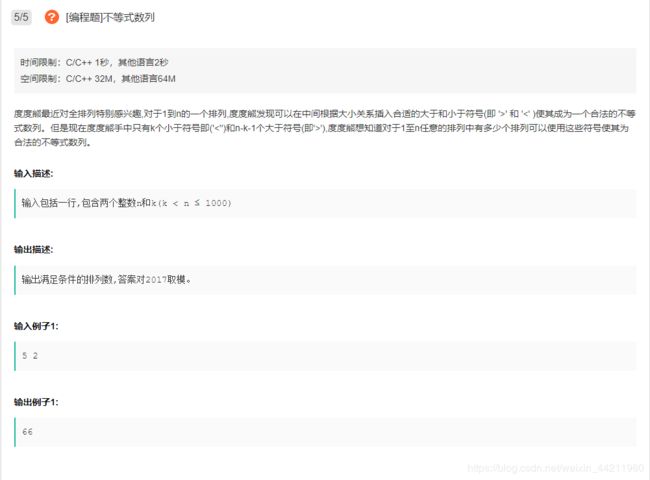
#include 【题5】
【解题思路】
https://www.nowcoder.com/questionTerminal/621e433919214a9ba46087dd50f09879?f=discussion by 赵翔
dp[i][j] = (dp[i - 1][j - 1] * (i - j) + dp[i - 1][j] * (j + 1)) % 2017;
**dp[i][j]**表示有i个数字及j个小于号所能组成的数量(大于号数量当然是i - j - 1次,后面需要使用)
而加入第i + 1个数字时,分以下四种情况:
1.如果将i+1插入当前序列的开头,即有了1<2,加入后成为3>1<2,会发现等于同时加入了一个大于号!(此时可以无视1与2之间的关系,因为i+1>i)
2.如果将i+1插入当前序列末尾,即1<2变成了 1<2<3,会发现等于同时加入了一个小于号! (此时可以无视1与2之间的关系,因为i+1>i)
3.如果将i+1加入一个小于号之间,即已经有 1<2了,向中间加入3,会发现变成了1<3>2,等于同时加入了一个大于号!
4.如果将i+1加入一个大于号中间,即有了2>1,变成了2<3>1,等于同时加入了一个小于号!
综上所述,**dp[i][j]**等于以上四种情况之和:
dp[i - 1][j] 将i加在开头等于加入一个大于号,即要求i-1个数时已经有了j个小于号
dp[i - 1][j - 1] 将i加在末尾等于加入一个小于号,即要求i-1个数时已经有了j-1个小于号
dp[i - 1][j] * j 将i加在任意一个小于号之间,等于加入了一个大于号;即要求i-1个数时已经有了j个小于号,每个小于号都可以进行这样的一次插入
dp[i - 1][j - 1] * (i- j - 1) 将i加载任意一个大于号之间,等于加入了一个小于号;即要求i-1个数时有了j-1个小于号,而此时共有
(i - 1) - (j - 1)- 1个大于号,每个大于号都要进行一次这样的操作合并同类项即为
dp[i][j] = (dp[i - 1][j - 1] * (i - j) + dp[i - 1][j] * (j + 1))
最后要记得取模
【AC代码】
#include