【数据结构】堆，大根堆，小根堆，优先队列 详解

堆

要了解堆之前,请先了解树,因为堆是一颗完全二叉树

如果不知道的话请点击下方链接了解

树,二叉树,完全二叉树详解

要注意的是

• 首先堆是一颗完全二叉树

• 其次堆中存储的值是偏序

Min-heap(小根堆): 父节点的值小于或等于子节点的值

Max-heap(大根堆): 父节点的值大于或等于子节点的值

好吧其实就是实现自动排序

O（logn）时间复杂度内实现插入，删除，O（1）查询

1.堆的数组实现

如果用数组来存储,那么儿子的编号便满足如下的性质

• 左儿子的编号是自己的编号的x2+1

• 右儿子的编号是自己的编号的x2+2

代码如下:

int heap[N],sz=0;
void push(int x)
{
    int i=sz++;
    while(i>0)//往上走
    {
        //父结点的编号
        int p=(i-1)/2;
        //如果不需要再交换就break;
        if(heap[p]<=x)break;
        heap[i]=head[p];
        i=p;
    }
    heap[i]=x;
}
//删除最小值：先把最小值丢掉，先把最后一个节点的值放到根节点处，然后排序交换即可
int pop()
{
    //最小值
    int ret=heap[0];
    int x=heap[--sz];
    int i=0;
    while(i*2+1<sz)//因为堆是完全二叉树偏左嘛
    {
        //左右儿子
        int a=i*2+1,b=i*2+2;
        //选出儿子中最小的
        if(b<sz&&heap[b]<heap[a])a=b;
        //如果不需要交换就break
        if(heap[a]>=x)break;
        //交换
        heap[i]=heap[a];
        i=a;
    }
    heap[i]=x;
    return ret;//返回被丢掉的那个最小值
}

2.小根堆

Min-heap(小根堆): 父节点的值小于或等于子节点的值

#include

template<typename item>
class smallest_heap{
    private:
        item heap[10001];
        int len;
    public:
        smallest_heap();
        void push(item const &);
        void pop();
        item top();
        int size();
        bool empty();

};

template<typename item>
smallest_heap<item>::smallest_heap(){
    len=0;
    memset(heap,0,sizeof(heap));
}

template<typename item>
void smallest_heap<item>::push(item const &n){
    heap[++len]=n;
    int son=len,father=son/2;
    while(heap[son]<heap[father] && father>=1){
        swap(heap[son],heap[father]);
        son=father,father=son/2;
    }
}

template<typename item>
void smallest_heap<item>::pop(){
    swap(heap[1],heap[len]);
    heap[len--]=0;
    int father=1,son=2;
    while(son<=len){
        if(son<len && heap[son]>heap[son+1]) son++;
        if(heap[father]>heap[son]){
            swap(heap[father],heap[son]);
            father=son,son=father*2;
        }else break;
    }
}

template<typename item>
item smallest_heap<item>::top(){
    return heap[1];
}

template<typename item>
int smallest_heap<item>::size(){
    return len;
}

template<typename item>
bool smallest_heap<item>::empty(){
    return len;
}

3.大根堆

Max-heap(大根堆): 父节点的值大于或等于子节点的值

#include

template<typename item>
class largest_heap{
    private:
        item heap[10001];
        int len;
    public:
        largest_heap();
        void push(item const &);
        void pop();
        item top();
        int size();
        bool empty();

};

template<typename item>
largest_heap<item>::largest_heap(){
    len=0;
    memset(heap,0,sizeof(heap));
}

template<typename item>
void largest_heap<item>::push(item const &n){
    heap[++len]=n;
    int son=len,father=son/2;
    while(heap[son]>heap[father] && father>=1){
        swap(heap[son],heap[father]);
        son=father,father=son/2;
    }
}

template<typename item>
void largest_heap<item>::pop(){
    swap(heap[1],heap[len]);
    heap[len--]=0;
    int father=1,son=2;
    while(son<=len){
        if(son<len && heap[son]<heap[son+1]) son++;
        if(heap[father]<heap[son]){
            swap(heap[father],heap[son]);
            father=son,son=father*2;
        }else break;
    }
}

template<typename item>
item largest_heap<item>::top(){
    return heap[1];
}

template<typename item>
int largest_heap<item>::size(){
    return len;
}

template<typename item>
bool largest_heap<item>::empty(){
    return len;

4.优先队列

在优先队列中，优先级高的元素先出队列。
标准库默认使用元素类型的<操作符来确定它们之间的优先级关系。
优先队列的第一种用法，也是最常用的用法：

priority_queue<int> q;

通过<操作符可知在整数中元素大的优先级高。
故示例1中输出结果为：9 6 5 3 2
第二种方法：
在示例1中，如果我们要把元素从小到大输出怎么办呢？
这时我们可以传入一个比较函数，使用functional.h函数对象作为比较函数。

priority_queue<int, vector<int>, greater<int>>q;

其中
第二个参数为容器类型。
第三个参数为比较函数。
故示例2中输出结果为：2 3 5 6 9

第三种方法：
自定义优先级。

struct node
{
    friend bool operator< (node n1, node n2)
    {
        return n1.priority< n2.priority;
    }
    int priority;
    int value;
};

在该结构中，value为值，priority为优先级。
通过自定义operator<操作符来比较元素中的优先级。
在示例3中输出结果为：
优先级值

9 5
8 2
6 1
2 3
1 4

但如果结构定义如下：

struct node
{
    friend bool operator> (node n1, node n2)
    {
        return n1.priority> n2.priority;
    }
    int priority;
    int value;
};

则会编译不过（G++编译器）
因为标准库默认使用元素类型的<操作符来确定它们之间的优先级关系。
而且自定义类型的<操作符与>操作符并无直接联系，故会编译不过。

例题

1.SP348 EXPEDI - Expedition（有趣的贪心思路，优先队列）

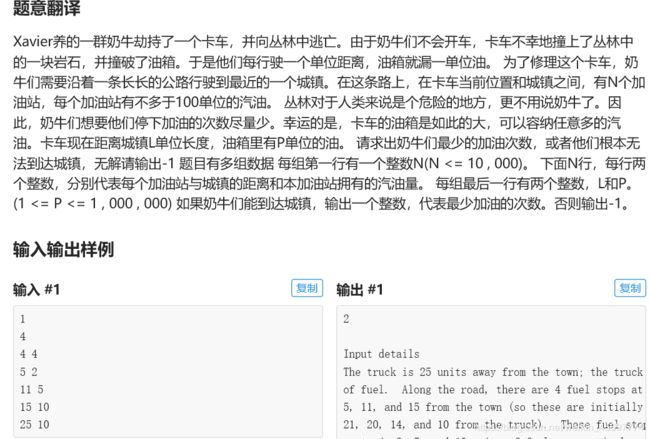
SP348 EXPEDI - Expedition（有趣的贪心，优先队列）

2.合并果子

合并果子
注：如果您通过本文,有(qi)用(guai)的知识增加了，请您点个赞再离开,如果不嫌弃的话,点个关注再走吧，日更博主每天在线答疑 ! 当然，也非常欢迎您能在讨论区指出此文的不足处，作者会及时对文章加以修正 !如果有任何问题，欢迎评论，非常乐意为您解答！( •̀ ω •́ )✧